Екзаменаційний білет № 12

1. Функції багатьох змінних. Диференціал та частинніпохiднi.

Арифметичним або -мірним простором будемо називати множину усіх можливих -мірних точок( , де - дійсні числа, які є і координатами точки в цьому просторі). В цьому просторі вводять понятття відстані між двома точками, норми, метрики, околу точки і т.і..

Приклад норми , відстань визначається як: .

Відображення називають функцією багатьох змінних і позначається .

називають відкритою кулею з центром в точці та радіуса , якщо:

, де це метрика в просторі .

Кажуть, що послідовність точок , -мірного простору збігається до точки , якщо збіжними є відповідні послідовності координат ,.., .

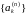– обмежана коли для неї коляобмежаного діаметра.

Для функції багатьох змінних виконується адаптована теорема Больцано-Вейштрассе:

З – можна виділити збіжну підпослідовність

Границя за Гейне має такий вигляд:

,

Подвійна границя позначається

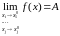
Повторна границя .

Лінійною формою називається лінійне відображення , -утворюють базис , ,

Ознфункція називається диференційованою в точці , якщо існує

Озн якщо для існує диференціал в точці ,то вектор-рядок називається повною похідною в точці .

Озн Диференціалом в точці для диференційованої ф-ї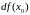 називається лінійне відображення

Озн Функція диф. на множині якщо вона диференційована в усіх точках цієї множини

Озн Частинною похідною ф-ї по змінній в точці :

Теорема (Достатні умови диф. вточці)

– неперервна в має в ньому усі частинні похідні, які є неперервними в диференційована в точці .

12.2Випадкове середнє та дисперсія. Емпiричнафункцiярозподiлу.

Озн. Вибірка - мат. модель незалежних вимірювань, що проводяться в однакових умовах.

Основною характеристикою вибірки є емпірична функція розподілу.

Озн. Емпірична функція розподілу - це функція вигляду

, де

інакше кажучи, це сума тих елементів вибірки, поділена на n, які попали лівіше,ніж n. Очевидно, що ця функція також випадкова.

Озн. Варіаційний ряд- елементи вибірки, розміщені в порядку зростання:

.

Озн. Кажуть, що послідовність випадкових величин збігається за ймовірністю до , якщо

,

та .

Має місце слідуюча теорема:

Теорема. Якщо F(x) - теоретична функція розподілу, то справедливе наступне твердження:

.

Доведення. Нехай x_k - довільний елемент вибірки. Розглянемо множини та . В схемі Бернуллі

р = F(x)=p, p = 1 - F(x) = q.

Тоді для кожного x емпірична функція розподілу буде показувати кількість успіхів, поділену на n, в схемі Бернуллі з n випробуваннями та характеристиками p та q. Далі, за законом великих чисел в схемі Бернуллі маємо

, що і доводить теорему.

Все.

Озн. Вибірковий момент 1-го порядку - вибіркове середнє визначається для вибірки з генеральної сукупності за формулою:

, а вибіркова дисперсія - центрований момент 2-го порядку:

².

Також мають місце слідуючі важливі теореми.

Теорема Глівенка.

Для довільної функції розподілу справедливе твердження

.

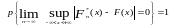Теорема Колмогорова.

Для довільної неперервної функції розподілу F(x) справедливе наступне твердження:

,

де K(z) - функція розподілу Колмогорова.

Тобто

K(z)=

Тобто якщо задати якесь значення і підібрати таке , що К( )= , то з ймовірністю (1- ) для всіх x :