1.9.5. Непрерывность функции нескольких переменных

Определение 1. Функция u=f(M) называется непрерывной в т. А, если .

Определение 2. Функция u=f(M) называется непрерывной на множестве , если она непрерывна в каждой точке этого множества.

Условию непрерывности можно придать разностную форму. Пусть

,

тогда условие непрерывности имеет вид:

.

(В примере 1 предыдущей темы рассмотрена непрерывная в нуле функция.)

Фиксируем все переменные, кроме одной, проложив, например, х₂=а₂,..., х_m=а_m. Тогда получим функцию одной переменной f(x₁,a₂,...,a_m), которая будет непрерывной в т. х₁=а₁, если f(x₁,...,x_m) непрерывна в т. А (очевидно). Таким образом, из непрерывности функции нескольких переменных в точке следует ее непрерывность по каждой координате (при фиксированных остальных). Обратное утверждение неверно, что показывает пример 2 предыдущей темы:

На координатных осях функция непрерывна (просто тождественно равна 0), но даже не имеет предела в т. (0,0). Непрерывности вдоль лучей также не достаточно для непрерывности в точке функции нескольких переменных. Это показывает пример 3 предыдущей темы.

1.8.9.1. Основные свойства непрерывных функций

1. Арифметические операции над непрерывными функциями приводят к непрерывным функциям (для частного знаменатель отличен от нуля).

2. Непрерывность сложной функции.

Пусть функции заданы на множестве Т  R^k, тогда каждой точке (t₁,...,t_k)  T ставится в соответствие число u по формулам , т.е. на множестве Т определена функция, которую мы назовем сложной функцией.

Пример 1. ; y=t ; x=t+s, тогда сложная функция имеет вид .

Теорема. Пусть имеет смысл сложная функция f(₁, ..., _m). Если функции ₁, ..., _k непрерывны в т. , а функция f непрерывна в т. , тогда сложная функция f(₁, ..., _k) непрерывна в т. t⁽⁰⁾.

По этой теореме функция непрерывна при всех (t,s)R².

3. Устойчивость знака непрерывной функции.

Теорема. Пусть функция u=f(M) непрерывна в т.А и f(A)0. Тогда существует такая -окрестность т.А, в которой f(M) имеет тот же знак, что и f(A).

4. Прохождение непрерывной функции через любое промежуточное значение.

Теорема. Пусть функция u=f(M) непрерывна на связном множестве . Тогда для любых точек А, В  и для любой кривой, L, соединяющей эти точки и лежащей в , найдется точка на этой кривой, в которой функция принимает любое заданное промежуточное значение между f(A) и f(B).

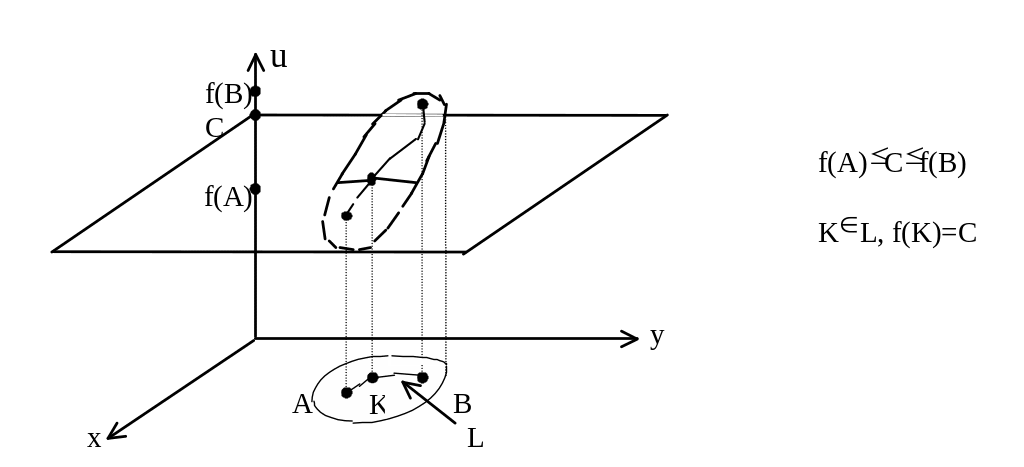
Условие связности существенно уже в одномерном случае:

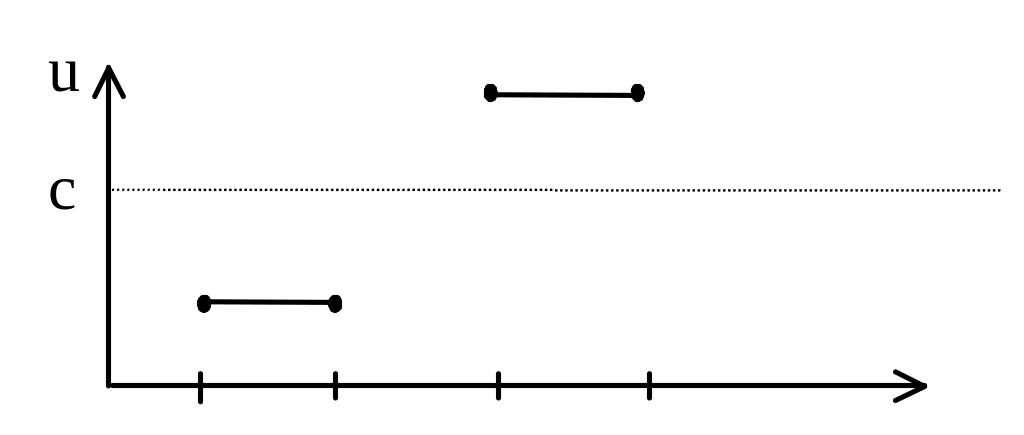
5. Теоремы Вейерштрасса.

Теорема 1. Функция, непрерывная на ограниченном замкнутом множестве, ограничена на этом множестве.

Теорема 2. Функция, непрерывная на ограниченном замкнутом множестве, достигает на этом множестве своих точных верхней и нижней граней. Для неограниченных или не замкнутых множеств эти утверждения неверны уже в одномерном случае.

1.9.6. Дифференцируемость функций нескольких переменных

1.9.6.1. Частные производные функций нескольких переменных

Пусть М(х₁, х₂, ..., х_m) внутренняя точка области определения функции u=f(x₁, ..., x_m). Пусть x_k - приращение k-ой координаты в данной фиксированной т.М, ему соответствует частное приращение функции

x_k u  f(x₁, ..., x_k-1, x_k+x_k, x_k+1, ..., x_m) - f(x₁, ..., x_m).

Рассмотрим отношение , которое зависит от x_k и определено при всех достаточно малых x_k, отличных от нуля.

Определение 1. Если существует , то он называется частной производной функции u=f(x₁, ..., x_m) в т. М(x₁, ..., x_m) по аргументу x_k и обозначается одним из символов: . Таким образом, .

Замечание. Так как изменяется только x_k + x_k, т.е. k-я координата аргумента функции f, то частная производная является обыкновенной производной функции f как функции только k-й переменной (при фиксированных остальных переменных). Это позволяет вычислить частные производные по одной из переменных по обычным формулам дифференцирования, если зафиксировать все остальные переменные.

Пример 1. u = x² + 3xy - y

вычисляем при условии, что y = const

вычисляем при условии, что x = const

Пример 2.

(при фиксированном у применима обычная теорема о производной сложной функции).

Аналогично

.

Выясним теперь, насколько полную информацию дают частные производные функции в данной точке о поведении функции в окрестности этой точки.

Сразу отметим, что частные производные в т.М₀ могут дать информацию о поведении функции только на прямых, проходящих через т.М₀ и параллельных координатным осям.

Конечно, этой информации совсем не достаточно, чтобы судить о поведении функции в целой окрестности т.М₀ (и, в частности, на других лучах, проходящих через т.М₀).

Пример функции показывает, что частные производные ее

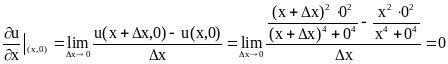
(аналогично )

существуют и обращаются в нуль не только в т. (0,0), но и всюду на координатных осях, а сама функция не имеет в т. (0,0) предела (см. тему 4). Заметим, что в одномерном случае из существования производной следовала непрерывность функции.

Таким образом, мы приходим к необходимости ввести более сильное условие, чем существование частных производных, чтобы оно было аналогом дифференцируемости функции одной переменной. Это условие должно быть связано с полным приращением функции в точке.