2.4Изоморфизм групп.

Группа G с операцией * называется изоморфной группе H с операцией , если существует взаимно однозначное соответствие , сохраняющее операции. То есть .

Например, группа G={0,1} с операцией сложение по модулю 2 изоморфна группе H={1,-1} с операцией умножения *.

Группа называется конечной, если число ее элементов конечно. Число элементов группы называется порядком группы.

Теорема 2.7. Конечная группа порядка n изоморфна некоторой подгруппе симметрической группы n-го порядка.

Доказательство. Перенумеруем элементы группы. Через обозначим номер элемента a. Отображение является взаимно однозначным, то есть перестановкой. Действительно, из равенства вытекает . Умножив последнее равенство справа на получаем , или i=j. Сопоставим элементу группы a перестановку . Указанное соответствие является взаимно однозначным. Действительно, из равенства перестановок вытекает равенство , которое выполняется только если . Умножив полученное равенство слева на получим a=b. Данное соответствие сохраняет операцию. Поскольку при произведении перестановок и имеем , то , т.е. отображение сохраняет операцию. Для доказательства теоремы осталось заметить, что множество перестановок вида образуют подгруппу в симметрической группе. Действительно, замкнутость по умножению показана выше, а замкнутость при взятии обратного элемента вытекает из равенства .

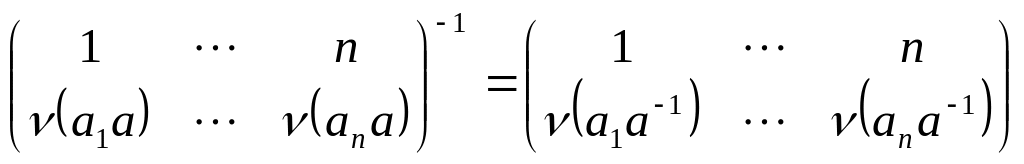Из приведенной теоремы вытекают простые факты:

1. С точностью до изоморфизма группа второго порядка единственна

2. С точностью до изоморфизма группа третьего порядка единственна

3. С точностью до изоморфизма существует только две группы четвертого порядка .

При больших n пользоваться данной теоремой затруднительно.

2.5Смежные классы, теорема Лагранжа

Пусть H подгруппа группы G. Левым смежным классом элемента a по подгруппе H называется множество элементов ah, где h принадлежит H. Левый смежный класс обозначают aH. Аналогично вводится правый смежный класс элемента a по подгруппе H, который обозначают Ha.

Поскольку в подгруппе всегда имеется нейтральный элемент, то каждый элемент a содержится в смежном классе aH (Ha).

Свойство 2.13. Элементы a и b принадлежат одному левому смежному классу по подгруппе H тогда и только тогда, когда

Доказательство. Если , то b=ah, и, значит, b принадлежит левому смежному классу aH. Обратно, пусть , тогда найдутся , что , и .

Теорема 2.8. Если левые (правые) смежные классы элементов a и b по подгруппе H имеют общий элемент, то они совпадают.

Доказательство. Пусть . Тогда найдутся , что . Произвольный элемент из левого смежного класса aH содержится в левом смежном классе bH. Действительно, для , и, следовательно, . Аналогично доказывается включение . Тем самым теорема доказана.

Следствие 2.8. Левые смежные классы либо не пересекаются, либо совпадают.

Доказательство очевидно.

Следствие 2.9. Левый (правый) смежный класс равномощен H.

Доказательство. Установим соответствие межу элементами подгруппы H и элементами смежного класса aH по формуле . Соответствие является взаимно однозначным. Тем самым утверждение доказано.

Теорема 2.9 (Лагранжа). Порядок конечной группы делится на порядок ее подгруппы.

Доказательство. Пусть G – группа порядка n, а H - подгруппа G порядка k.Имеет место равенство . Удалим из правой части равенства повторяющиеся члены. В результате останутся не пересекающиеся смежные классы. Поскольку число элементов в смежном классе равно , то , где m количество различных смежных классов. Тем самым установлено равенство n=mk, что и требовалось.

Количество различных смежных классов называется индексом подгруппы H в группе G.