
- •1Структура линейного преобразования.
- •1.1Аннулирующий многочлен вектора, пространства
- •1.2Расщепление пространства в прямую сумму инвариантных подпространств
- •1.3Корневые подпространства.
- •1.4Жорданова клетка. Циклический базис. Циклические пространства.
- •1.5Жорданов базис, существование и единственность.
- •1.6Построение Жорданова базиса.
- •2 Алгебра, полугруппы, группы
- •2.1Отношение, операция, алгебра.
- •2.2Полугруппа
- •2.3Группа, подгруппа
- •2.4Изоморфизм групп.
- •2.5Смежные классы, теорема Лагранжа
- •2.6Циклические группы.
- •Циклические группы одинаковых порядков изоморфны между собой.
- •Циклическая группа бесконечного порядка изоморфна группе целых чисел.
- •Любая подгруппа циклической группы циклическая.
- •2.7Нормальный делитель, факторгруппа.
- •2.8Гомоморфизм групп.
- •2.9Нормальный ряд
- •2.10Простота знакопеременной группы
- •3Кольцо, подкольцо, идеал, факторкольцо.
- •3.1Кольцо
- •3.2.4Поле частных
- •3.3Идеал, факторкольцо.
- •3.3.1Кольцо вычетов.
- •3.3.2Присоединение корня многочлена.
- •3.4Гомоморфизм колец.
- •4Характеристика поля. Конечные поля.
- •4.1Характеристика тела, поля.
- •4.2Простые расширения полей
- •4.3Конечные поля.
- •5Теория Галуа
- •6.1Кольцо матриц. Эквивалентность матриц.
- •Перестановка строк
- •Умножение строки на обратимый элемент кольца
- •Прибавление к строке строки , умноженной на элемент кольца .
- •6.2Кольцо многочленов с матричными коэффициентами.
3.4Гомоморфизм колец.
Однозначное
отображение кольца K
в кольцо H,
сохраняющее операции сложения и
умножения, называется гомоморфизмом
колец (![]() и
и
![]() ).
).
Свойство 3.23.
![]() ,
,
![]() .
.
Множество
элементов кольца K,
образ которых равен 0, называют ядром
гомоморфизма и обозначают
![]() ,
а множество элементов H,
для которых существует прообраз, называют
множеством образов и обозначают
,
а множество элементов H,
для которых существует прообраз, называют
множеством образов и обозначают
![]() .
.
Свойство 3.24.
![]() - двусторонний идеал в K
- двусторонний идеал в K
Доказательство.
Пусть
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
Аналогично,
.
Аналогично,
![]() ,
и
,
и
![]() .
Далее,
.
Далее,
![]() ,
то есть
,
то есть
![]() .
Тем самым установлено, что
.
Тем самым установлено, что
![]() - подкольцо. Для
- подкольцо. Для
![]() имеем
имеем
![]() ,
то есть
- двусторонний идеал в K.
,
то есть
- двусторонний идеал в K.
Свойство 3.25.
![]() - подкольцо H
- подкольцо H
Доказательство.
Пусть
![]() ,
тогда найдутся их прообразы c,d
и так далее…
,
тогда найдутся их прообразы c,d
и так далее…
Теорема 3.22.
Факторкольцо
![]() изоморфно
.
Для любого двустороннего идеала I
кольца K
существует гомоморфизм с ядром равным
I,
например, в K/I.
изоморфно
.
Для любого двустороннего идеала I
кольца K
существует гомоморфизм с ядром равным
I,
например, в K/I.
Доказательство.
Изоморфизм задается соотношением
![]() .
.
4Характеристика поля. Конечные поля.
4.1Характеристика тела, поля.
Пусть P произвольное поле (тело). Обозначим через e нейтральный элемент. Под ke будем понимать сумму e+e+…+e, k – указатель кратности.
Рассмотрим циклическую группу относительно +, порожденную e. Если группа бесконечна, то говорят, что поле P имеет характеристику 0. В этом случае поле содержит подполе изоморфное полю рациональных чисел.
Пусть порядок группы равен n. Поскольку (ke)(me)=(km)e, то множество элементов вида ke образует подполе поля P, которое изоморфно Zn. В этом случае число n – простое и называется характеристикой поля.
Оформим сказанное выше в виде теоремы.
Теорема 4.23.
Поле характеристики ноль содержит
подполе, изоморфное полю рациональных
чисел. Поле конечной характеристики n
содержит подполе изоморфное кольцу
вычетов
![]() .
.
4.2Простые расширения полей
Пусть поле P
содержится в поле T
и a
– элемент
T
не принадлежащий P.
Рассмотрим наименьшее поле P(a)
содержащее все элементы из P
и a.
Все элементы вида
![]() принадлежат P(a).
Рассмотрим два случая.
принадлежат P(a).
Рассмотрим два случая.
Ни один элемент вида не равен 0. Тогда поле P(a) изоморфно полю частных P(x). В этом случае говорят о трансцендентном расширении полей.
Найдется
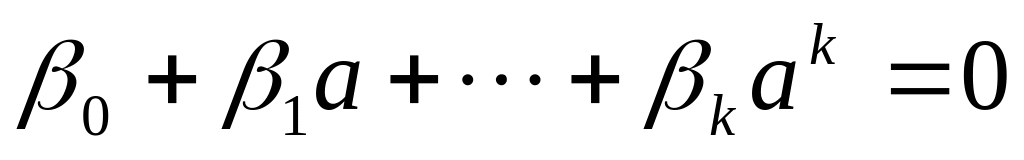 .
Выберем элемент с наименьшей степенью.
Многочлен
.
Выберем элемент с наименьшей степенью.
Многочлен
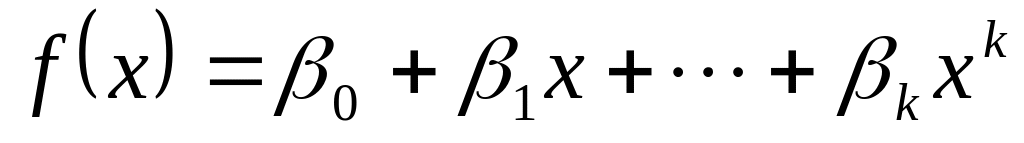 неприводим и поле P(a)
изоморфно факторкольцу
неприводим и поле P(a)
изоморфно факторкольцу
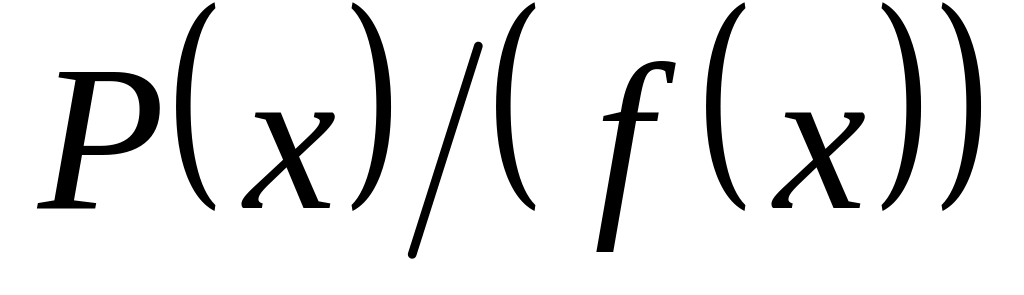 .
В этом случае говорят об алгебраическом
расширение полей.
.
В этом случае говорят об алгебраическом
расширение полей.
4.3Конечные поля.
Теорема 4.24. Число элементов конечного поля pn, где p – простое число.
Доказательство. Поскольку поле P конечно, то его характеристика отлична от нуля. Пусть p его характеристика. Поле P, можно рассматривать как векторное пространство над Zp. Обозначим через v1,…,vn базис P. Любой элемент поля P однозначно характеризуется координатами (x1,…,xn ) в этом базисе. Каждая координата принимает p значений, следовательно, число различных наборов координат, а значит и элементов поля P, равно pn.
Лемма 4.2
В поле характеристики p
![]() .
.
Доказательство.
![]() ,
где
,
где
![]() - кратность вхождения элемента. Величина
- кратность вхождения элемента. Величина
![]() не делится на p
только в случае i=0;p.
Так как pe=0,
то
.
не делится на p
только в случае i=0;p.
Так как pe=0,
то
.
Теорема 4.25. Для любого натурального n и простого p существует поле порядка pn.
Расширим
Zp
так, чтобы результирующее поле содержало
все корни многочлена
![]() .
Многочлен не имеет кратных корней, так
как его производная равна –1. Обозначим
через M
множество корней многочлена
.
Легко проверить, что M
является полем и число его элементов
равно pn
.
Многочлен не имеет кратных корней, так
как его производная равна –1. Обозначим
через M
множество корней многочлена
.
Легко проверить, что M
является полем и число его элементов
равно pn
Теорема 4.26.
Поле порядка
![]() единственно с точностью до изоморфизма.
единственно с точностью до изоморфизма.
Доказательство.
Поскольку
число элементов поля
,
то его характеристика равна
![]() .
Следовательно, любое поле P
порядка
можно рассматривать как расширение
кольца вычетов
.
Мултьипликативная группа поля (
.
Следовательно, любое поле P
порядка
можно рассматривать как расширение
кольца вычетов
.
Мултьипликативная группа поля (![]() )
имеет порядок
)
имеет порядок
![]() ,
и, следовательно, для любого
справедливо
,
и, следовательно, для любого
справедливо
![]() .
Таким образом, все элементы поля являются
корнями уравнения
.
Таким образом, все элементы поля являются
корнями уравнения
![]() над
.
над
.
Теорема 4.27. Мультипликативная группа корней n-ой степени из 1 в поле P является цикличной.
Доказательство.
Пусть p
характеристика поля P.
Если
![]() ,
то
,
то
![]() ,
и, значит, множество корней уравнения
,
и, значит, множество корней уравнения
![]() совпадает с множеством корней степени
совпадает с множеством корней степени
![]() .
Не нарушая общности можно считать
.
Не нарушая общности можно считать
![]() .
Доказательство достаточно провести
для случая, когда все корни n-ой
степени из 1 содержатся в поле P.
В противном случае расширим поле и
воспользуемся фактом, что любая подгруппа
циклической группы – циклическая.
Поскольку
.
Доказательство достаточно провести
для случая, когда все корни n-ой
степени из 1 содержатся в поле P.
В противном случае расширим поле и
воспользуемся фактом, что любая подгруппа
циклической группы – циклическая.
Поскольку
![]() имеет только единственный корень, равный
нулю, то количество корней n-ой
степени из 1 равно n.
Рассмотрим три случая:
имеет только единственный корень, равный
нулю, то количество корней n-ой
степени из 1 равно n.
Рассмотрим три случая:
n – простое число. Тогда группа корней имеет порядок n, и, значит циклическая
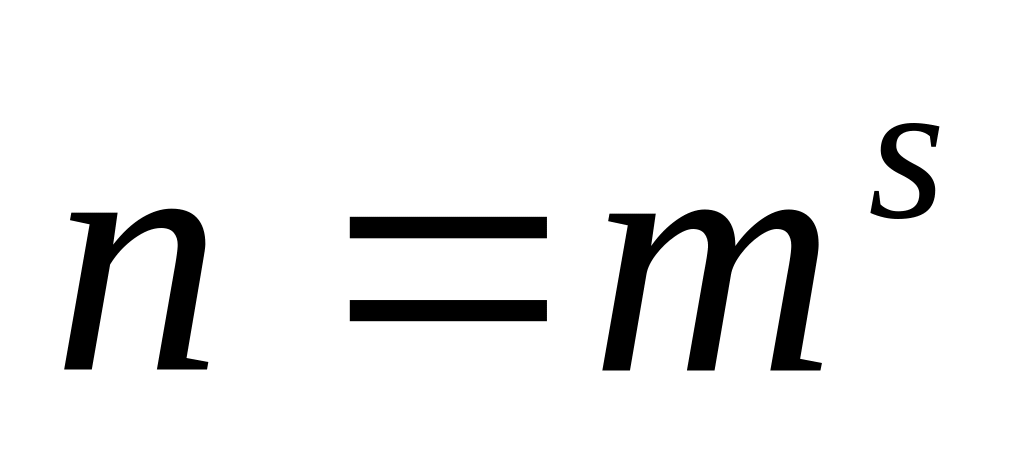 -
степень простого числа. Найдем корень
уравнения
,
не являющийся корнем уравнения
-
степень простого числа. Найдем корень
уравнения
,
не являющийся корнем уравнения
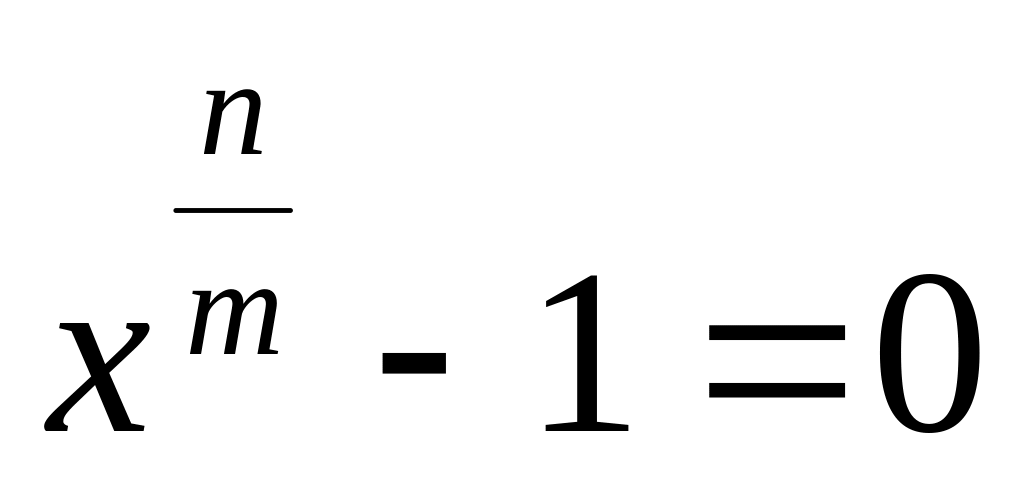 .
Порядок элемента
является делителем порядка группы n
и не является делителем
.
Порядок элемента
является делителем порядка группы n
и не является делителем
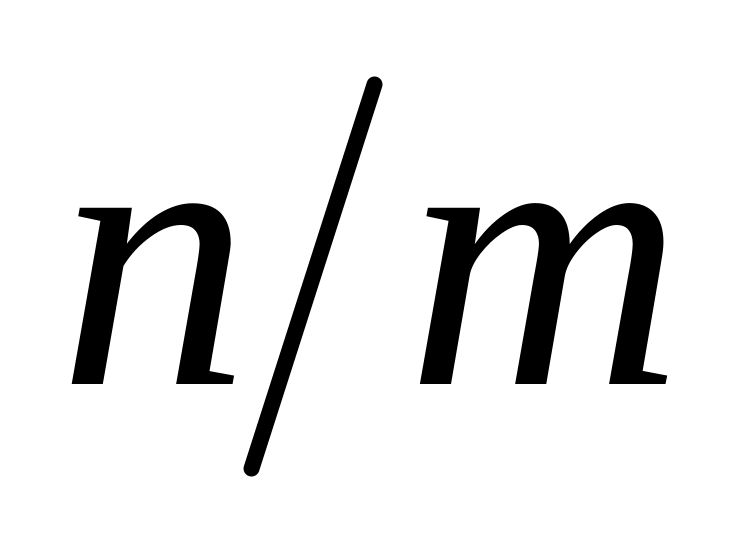 .
Следовательно, порядок
равен n
и группа циклическая.
.
Следовательно, порядок
равен n
и группа циклическая.Пусть
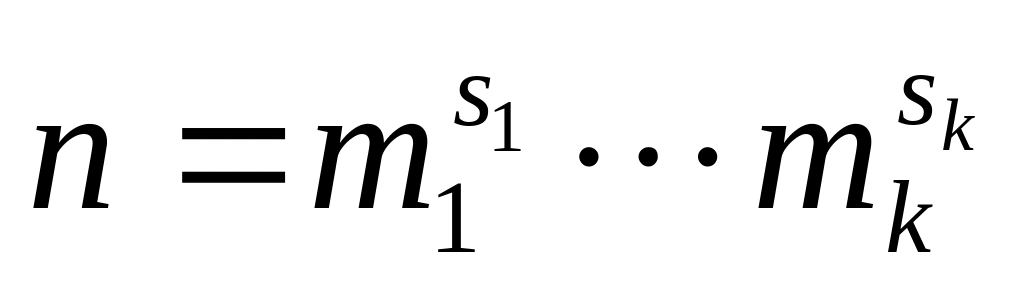 .
Обозначим через
порождающий элемент циклической группы
корней из 1 степени
.
Обозначим через
порождающий элемент циклической группы
корней из 1 степени
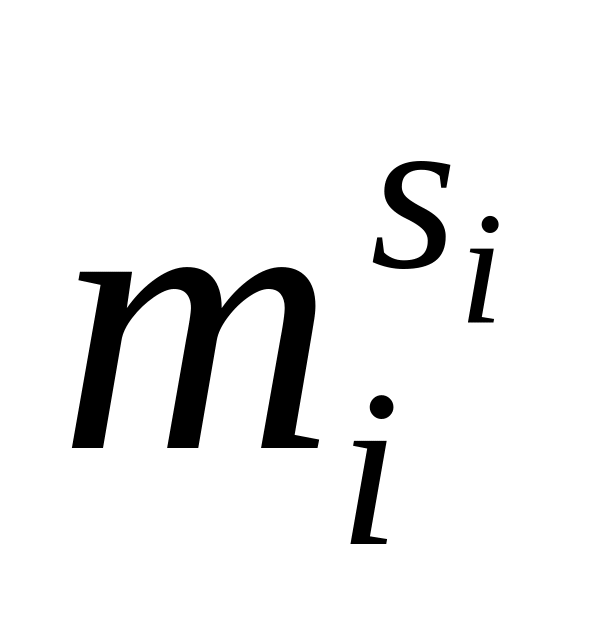 .
Положим
.
Положим
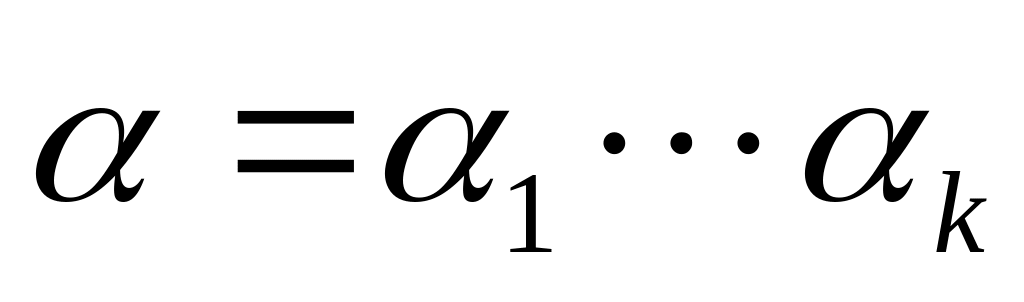 .
Индукцией по k
покажем, что порядок
равен
.
Индукцией по k
покажем, что порядок
равен
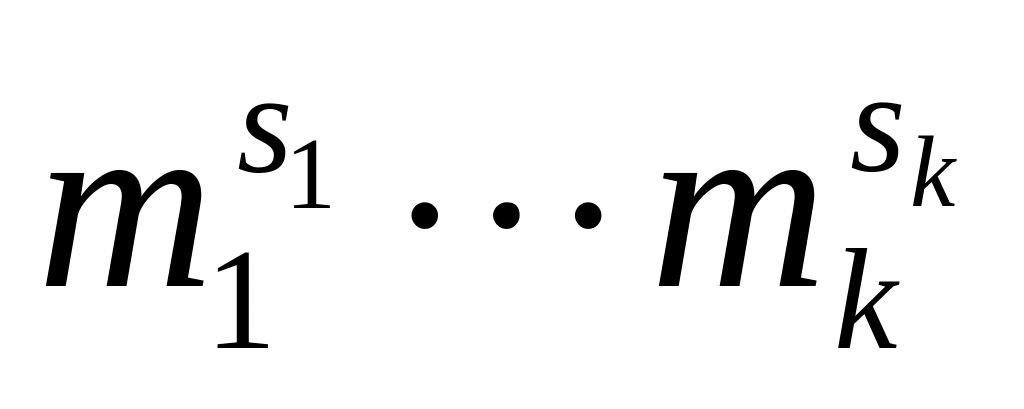 .
При k=1
утверждение очевидно. Пусть оно доказано
для k-1.
Порядок элемента
.
При k=1
утверждение очевидно. Пусть оно доказано
для k-1.
Порядок элемента
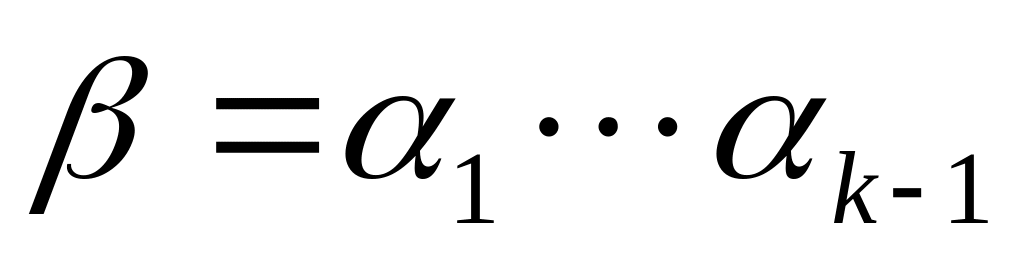 равен
равен
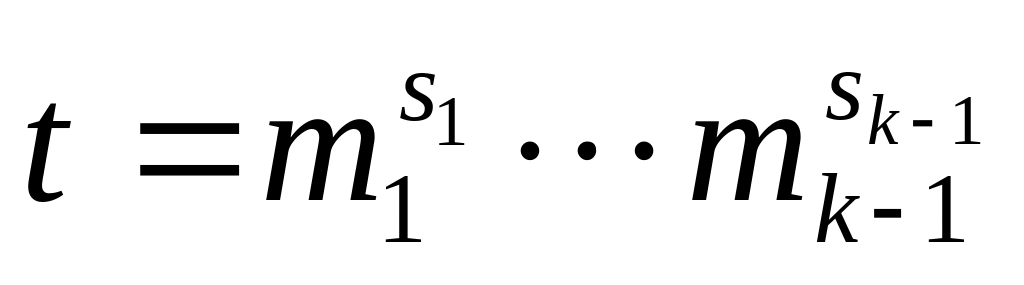 .
Наибольший общий делитель t
и
.
Наибольший общий делитель t
и
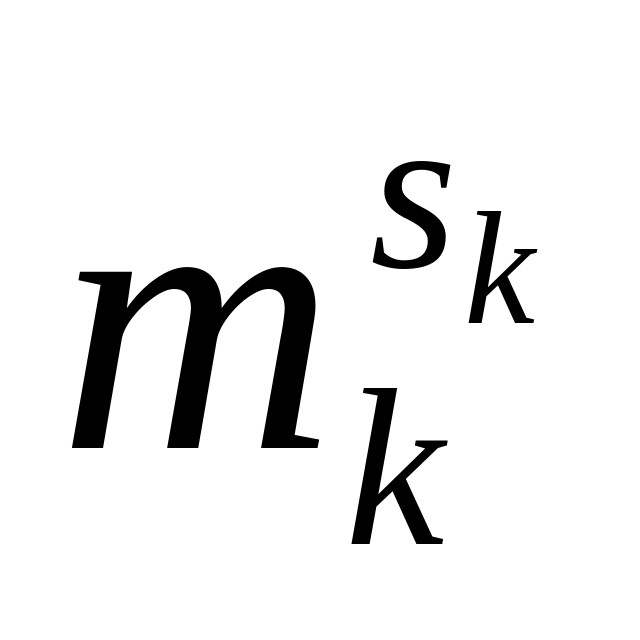 равен 1, и, значит, найдутся числа u
и v,
что
равен 1, и, значит, найдутся числа u
и v,
что
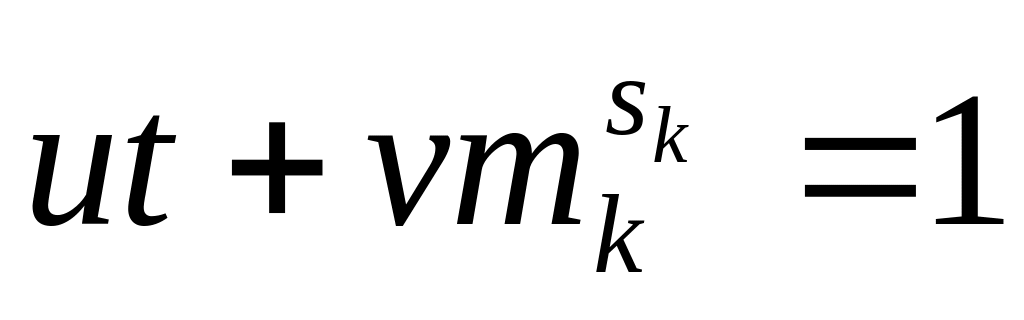 .
Поскольку
.
Поскольку
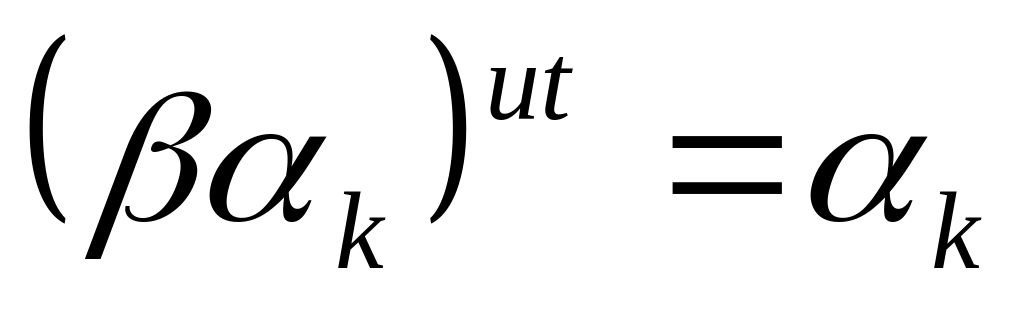 и
и
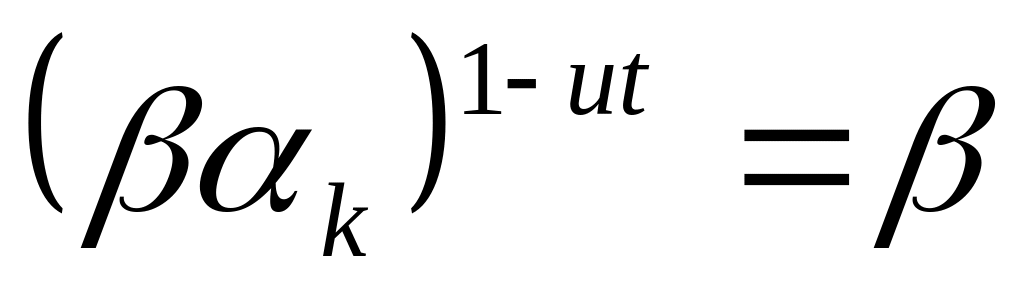 ,
то порядок элемента
,
то порядок элемента
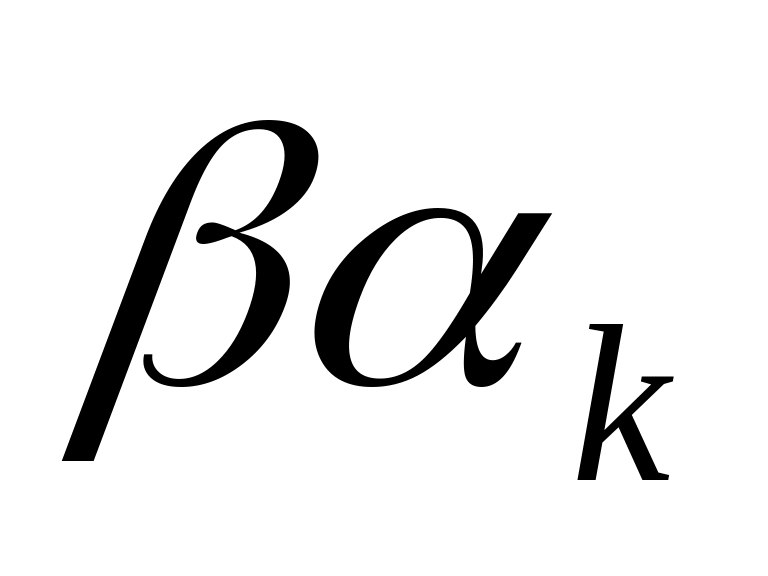 делится на t
и на
.
Далее, из равенства
делится на t
и на
.
Далее, из равенства
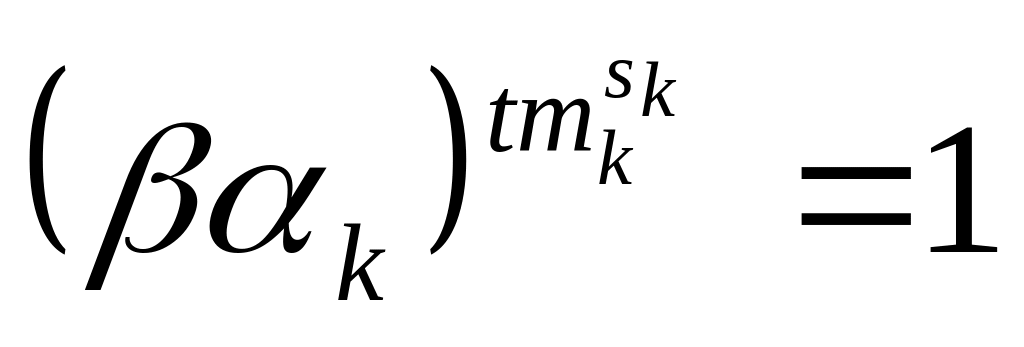 ,
следует, что порядок элемента
,
следует, что порядок элемента
 является делителем
является делителем
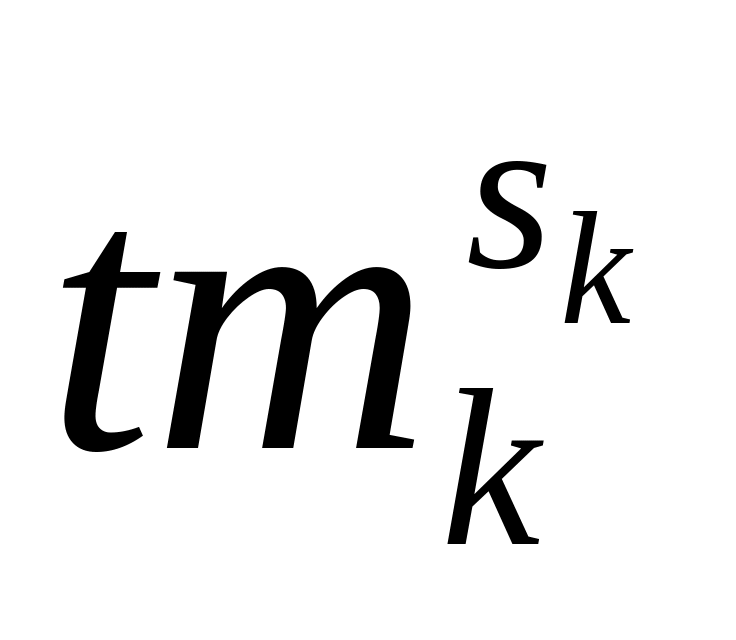 .
Теорема доказана.
.
Теорема доказана.
