18 Уравнения, допускающие понижение порядка

одним из методов интегрирования ДУ высших порядков является ме-тод понижения порядка. Суть метода состоит в том, что с помощью заме-ны переменной (подстановки) данное ДУ сводится к уравнению, порядок которого ниже.

Рассмотрим три типа уравнений, допускающих понижение порядка.

I. Пусть дано уравнение

Порядок можно понизить, введя новую функцию р(х), положив у^'=р(х). Тогда у^''=p^'(x) и получаем ДУ первого порядка: p^'=ƒ(х). Решив его, т. е. найдя функцию р=р(х), решим уравнение y^'=р(х). Получим общее решение заданного уравнения (3.6).На практике поступают иначе: порядок понижается непосредственно путем последовательного интегрирования уравнения.Так как  уравнение (3.6) можно записать в виде dy^'=ƒ(х) dx. Тогда, интегрируя уравнение y^''=ƒ(х), получаем: y^'= или y^'=1 (x)+с₁. Далее, интегрируя полученное уравнение по х, находим: - общее решение данного уравнения. Если дано уравнение то, проинтегрировав его последовательно n раз, найдем общее решение уравнения:

19. Линейные ду n-го порядка(однородные и неоднородные). Действительные и комплексные решения однородного линейного уравнения и их свойства

Линейное Ур-е n-го порядка имеет вид: 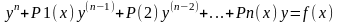(1)

Предполагаем что p1(x), p2(x)…. Pn(x),f(x) непрерывны на (а; в) данное предположение обеспечивает единственность решения задачи коши.

Линейный дифференциальный оператор n-го порядка

Левую часть Ур-я (1) обозначим как 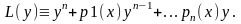(2)

Таким образом L(y) есть результат выполнения над функцией у операций указанных в правой части выражения 2

Совокупность этих операций обознацим L.

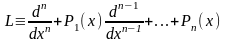и будем называть его линейным дифференциальным оператором n-го порядка. Он обладает следующими свойствами:

1.L(k*y)=k*L(y)

2. L(y1+y2)=L(y1)+L(y2)

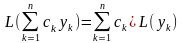
Те получим что L(y)=f(x)

Если F(x)=0 то уравнение однородное если же нет то не однородное.

Действительные и комплексные корни однородногшо линейного уравнения

Пусть даны 2 действительные функции U(x) и V(x) тогда функцию y(x)= U(x)+iV(x)

Будем называть комплексной функцией от действительнойпеременной х на интервале(а, в) при этом U(x) действительная часть а V(x) мнимая. Р/м понятие производной от комплексной функции действительной переменной. Пусть действительная и мнимая части компл функц имеют производную к-го порядка тогда производная к-го порядка определена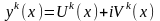

Используя полученую формулу можно вычислить знач оператора L от комплексной функции у(х)

L(y(x))=L(U(x))+iL(V(x))

Те значение оператора L от комплексной функции у(х) является так же комплексной функцией действительной переменной х при этом действительная часть L(y(x))=L(U(x))

А мнимая L(y(x))= iL(V(x))

В результате мы можем дать понятие о комплексном решении однородного лин урав L(y)=0

Комплексная функция у(х) называеться решением уравнения L(y)=0 в интервале (а, в) если она обращает это уравнение в тождество те

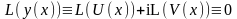
(а<x<в) воспользовавшись линейностью L и определение производной линейной функции получим L(U(x))+iL(V(x))=0 следовательно 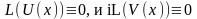а это значит что функция U(x) и V(x) являются решениями однородного уравнения L(y)=0 таким образом действительная и мнимая части комплексного решения однородного линейного уравнения являются действительными решениями этого уравнения. Те знание одного комплексного решения дает возможность найти 2 действительных

Свойства:

1. если у1=у1(х) частное решение урав L(y)=0 то и у1=су1(х) где с постоянная тоже частное решение этого уравн

2. если у1=у1(х) и у2=у2(х) являются частными решениями урав L(y)=0 то их сунна у1+у2 =у тоже являеться частным решением

3. если у1,у2,у3…..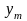 частные решения урав L(y)=0то и 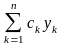где Ск постоянная так же является решением урав L(y)=0.

20 Фунд. система решений построение общего решения однородного линейного уравнения.

Расм системк из n реш-ий однор ур-я (1)

y(x₁) y₂(x)…y_n(x) (12)

Такая система ф-ий наз. фунд. если это ф-ии лин. независ между собой. Эти ф-ии реш-е однор. ур-я 2) Их обязат. n штук 3)Лин. независ. они

Докаж что фун. сист реш-ий ет. Выберем произв. квадратичную невыраженную матр.

Определим ф-ии y₁(x)…y_n(x), так что y₁(х₀)=y⁰₁ y_n(x₀)=y⁰_n

y₁(х₀)=y⁰₁

y^(n-1)₁(x₀)=y^0(n-1)₁

По нелокальной Th эти ф-ии  и они лин независ т.к. в противном случае столбцы матр. Y(x) буд. лин. завис между собой, что противоречит предп. что Y₀

Пришли к противореч. ЧТД

Утв2: Если ф-ии в сист (12) лин. независ , то опр Вронского ни в одной точке не обр. в 0. Для произв. сист. ф-ий это утв. неверно.

Д-во Пусть ф-я y₁(x)…y_n(x) лин. независ , но  х₀(a,b) котор W(x₀)=0.Тогда можно зап-ть след сист.  c₁…c_n:

система из (n-1) ур-й (14):

c1y₁(x0)+…+cnyn(x0)=0

c1y1’(x0)+…+cnyn’(x0)=0

……………………………………………………

c1y1^(n-1)(x)+…+cnyn^(n-1)(x)=0

Эта сист. для нах-я констант т.к. они явл. неизв. обознач. через с₁,с₂…с_n реш-е системы (14) это реш-е ненулевое и оно , т.к. определитем этой системы явл. опред-ль Вронского

y⁰ (x)=c⁰₁y₁(x)+c⁰₂y(x)+…+c⁰_ny_n(x) (16)

Если нач. усл. для этой ф-ии y⁰ (x₀)=0 y(x₀)=0 y^(n-1)(x₀)=0

y(x₀)0 (*)  c⁰₁y₁(x)+…+c⁰_ny_n(x)0 (16)

По сл-ю из нелокальной Th ф-я котор удовл нул нач есть тожд 0 т.е. (*) что противоречит лин зав ф-ии y₁…y_n ЧТД

Построение общего решения однородного линейного уравнения по ФСР

Знание ФСР уравнения L(y)=0 дает возможность построить общее решение этого уравнения.

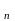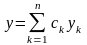Теорема: если функции у1,…у образуют ФСР однор лин уравн n-го порядка в интервале (а, в) те в интервале непрерывности коэффициентов Pn(х) то функция дает общее решение этого уравнения в области а<x<в .