Решение уравнения Шрёдингера

Решение уравнения Шрёдингера для водородного атома использует факт, что кулоновский потенциал является изотропным, то есть не зависит от направления в пространстве, другими словами обладает сферической симметрией. Хотя конечные волновые функции (орбитали) не обязательно сферически симметричны непосредственно, их зависимость от угловой координаты следуют полностью из этой изотропии основного потенциала: собственные значения оператора Гамильтона можно выбрать в виде собственных состояний оператора углового момента. Это соответствует тому факту, что угловой момент сохраняется при орбитальном движении электрона вокруг ядра. Отсюда следует, что собственные состояния гамильтониана задаются двумя квантовыми числами углового момента l и m (целые числа). Квантовое число углового момента l может принимать значения 0, 1, 2… и определяет величину углового момента. Магнитное квантовое число может принимать m = −l, .., +l определяет проекцию углового момента на (произвольно выбранную) ось z.

В дополнение к математическим выражениям для волновых функций полного углового момента и проекции углового момента, нужно найти выражение для радиальной зависимости волновой функции. В потенциале 1/r радиальные волновые функции записываются с использованием полиномов Лагерра). Это приводит к третьему квантовому числу, которое называется основное квантовое число n и может принимать значения 1, 2, 3… Основное квантовое число в атоме водорода связано с полной энергией атома. Заметим, что максимальное значение квантового числа углового момента ограничена основным квантовым числом: оно может изменяться только до n − 1, то есть l = 0, 1, …, n−1.

Из-за сохранения углового момента, состояния с тем же l, но различными m имеют ту же самую энергию (это выполняется для всех проблем с аксиальной симметрией. Кроме того, для водородного атома, состояния с тем же самым n, но разными l также вырождены (то есть, они имеют ту же самую энергию). Однако, это — определенная особенность атома водорода и не верно для более сложных атомов, которые имеют (эффективный) потенциал, отличающийся от кулоновского (из-за присутствия внутренних электронов, экранирующих потенциал ядра).

Если мы примем во внимание спин электрона, то появится последнее квантовое число, проекция углового момента собственного вращения электрона на ось Z, которая может принимать два значения. Поэтому, любое собственное состояние электрона в водородном атоме описывается полностью четырьмя квантовыми числами. Согласно обычным правилам квантовой механики, фактическое состояние электрона может быть любой суперпозицией этих состояний. Это объясняет также, почему выбор оси Z для квантования направления вектора углового момента является несущественным: орбиталь для данных l и m ', полученных для другой выделенной оси Z ', всегда представляется как подходящая суперпозиция различных состояний с разными m (но тем же самым l), которые были получены для Z.

Рассмотрим сейчас решение уравнения Шредингера для атома водорода. Так как потенциальная функция электрона в атоме водорода имеет вид , где e — заряд электрона (и протона), r — радиус вектор, уравнение Шредингера запишется следующим образом:

Здесь ψ — волновая функция электрона в системе отсчёта протона, m — масса электрона, где ,  — постоянная Планка, E — полная энергия электрона,  — оператор Лапласа. Так как потенциальная функция зависит от r, а не от координат по отдельности, удобно будет записать лапласиан в сферической системе координат (r,θ,ϕ). В ней он выглядит следующим образом:

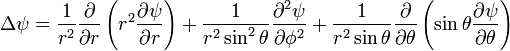
И уравнение Шредингера в сферических координатах:

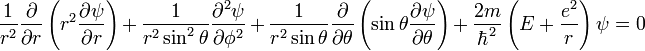
В этом уравнении ψ — функция трех переменных (r,θ,ϕ). Разделим его на три более простых уравнения. Для этого представим функцию ψ(r,θ,ϕ) как произведение трех функций: ψ(r,θ,ϕ) = R(r)Θ(θ)Φ(ϕ). Эти функции будем обозначать просто R,Θ,Φ. Тогда

.

После подстановки значений частных производных в уравнение Шредингера получим:

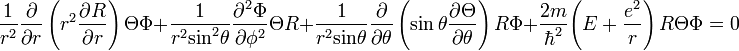
Умножим уравнение на :

Второе слагаемое тут зависит только от . Перенесем его в правую часть равенства.

Равенство возможно, когда обе части равны какой-то постоянной величине. Обозначим ее . Следовательно,

Решением этого уравнения являются функции

Угол может изменяться от 0 до 2π. Функция Φ должна быть периодической с периодом 2π. Это возможно только если Таким образом, из решения уравнения Шредингера получаем значение одного из квантовых чисел (конечно, можно получить из него их все). Число m_l называется магнитным квантовым числом.

Далее, интегрируя квадрат модуля функции Φ от 0 до 2π и приравнивая полученное выражение 1, получим что .

Далее рассмотрим левую часть уравнения . Она, конечно, равна :

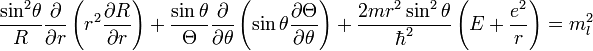
Разделим уравнение на sin ²θ:

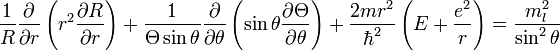
После аналогичного вышеуказанному перенесению второго слагаемого в правую часть и обозначения величины, которой равны эти части, через β, получаем

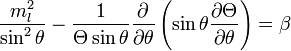
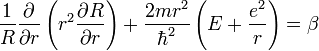
Решение этих двух последних уравнений приводит к значениям и n соответственно. 3 квантовых числа в совокупности полностью описывают состояния электрона в атоме водорода.

Модуль полной энергии электрона в стационарном состоянии в атоме водорода обратно пропорционален n². Число n называется главным квантовым числом. Оно может иметь значения от 1 до . Его связь с энергией см. ниже.

Число называется азимутальным квантовым числом и определяет момент количества движения электрона и форму электронного облака; может иметь значения от 0 до n − 1 (n здесь относится к энергетическом уровню, на котором находится рассматриваемый электрон).

Магнитное квантовое число m_l определяет проекцию момента количества движения на выбранную ось в магнитном поле. Эта проекция равна .

Математическое описание атома водорода

Энергетический спектр

Энергетические уровни атома водорода, включая тонкую структуру записываются в виде

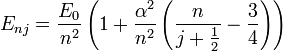
где

 — постоянная тонкой структуры

 — собственное значение оператора полного момента импульса

Энергию можно найти в простой модели Бора, с массой электрона и зарядом электрона :

где электронвольты, джоули, постоянная Планка, диэлектрическая проницаемость вакуума.

Волновые функции

В сферических координатах волновые функции имеют вид:

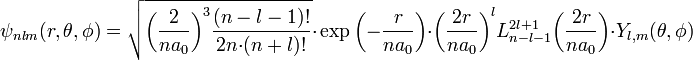
где:

 — Боровский радиус.

 — обобщённые полиномы Лагерра степени от функции .

 — нормированные на единицу сферические функции.

Угловой момент

Собственные значения для оператора углового момента:

Нахождение энергии электрона из модели Бора

Вычислим уровни энергии атома водорода без учета тонкой структуры, используя простую модель атома Бора. Для этой цели можно сделать грубое допущение электрона, двигающегося по круговой орбите на фиксированном расстоянии. Приравнивая кулоновскую силу притяжения центростремительной силе получим:

Здесь масса электрона, его скорость на орбите радиуса , диэлектрическая проницаемость вакуума (электрическая постоянная).

Отсюда кинетическая энергия электрона

где расстояние от электрона до ядра.

Потенциальная его энергия

Полная энергия, соответственно, равна

Для нахождения радиуса стационарной орбиты с номером рассмотрим систему уравнений, в которой второе есть математическое выражение первого постулата Бора :

Отсюда получаем выражение для радиуса стационарной орбиты с номером :

Радиус первой орбиты оказывается равным метра. Эта константа называется боровским радиусом.

Подставляя это значение в выражение для энергии, получим, что

Отсюда мы можем найти волновое число (по определению это обратная длина волны или число длин волн, укладывающихся на 1см) фотона, излучаемого атомом водорода за один переход из возбужденного состояния с главным квантовым числом в состояние с неким фиксированным главным квантовым числом .

где постоянная Ридберга (имеет размерность см⁻¹).