4. Игра 2 X 2

Эта игра является наиболее простым случаем конечной игры где у каждого игрока две стратегии.

Рассмотрим игру 2 X 2 с матрицей:

Ai/Bj	B1	B2
A1
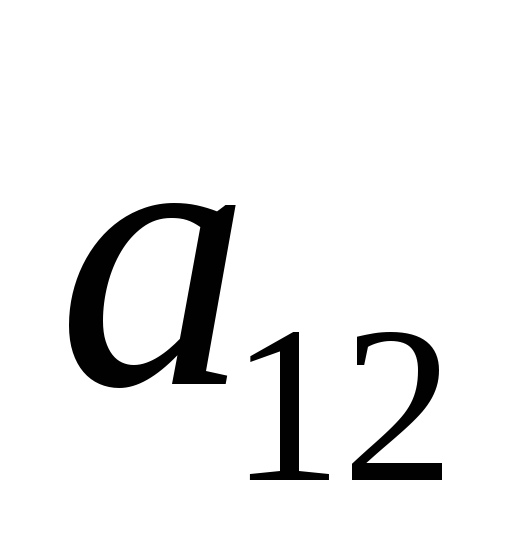
A2

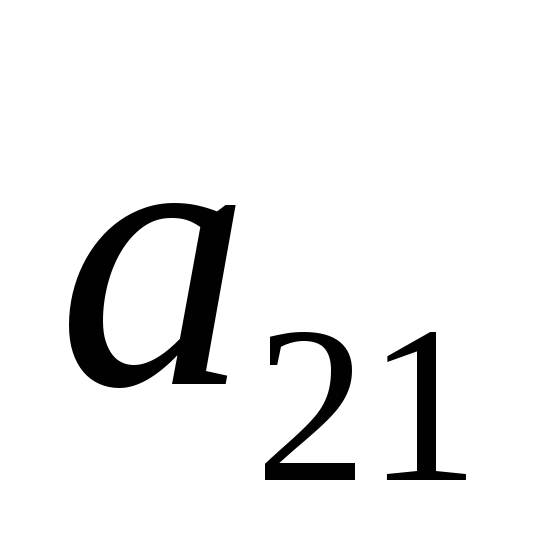
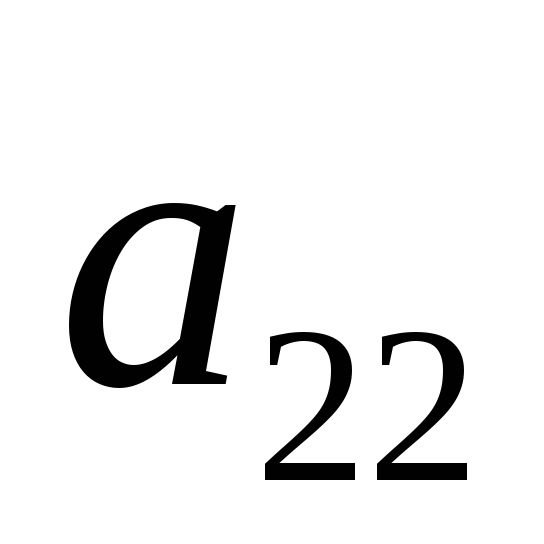
Здесь могут встретиться два случая:

1. Игра имеет седловую точку.

2. Игра не имеет седловой точки.

В первом случае решение очевидно - это пара стратегий пересекающихся в столбцах.

Рассмотрим второй случай, при этом нижняя цена игры не равна верхней (не равна).

Найдем это решение, то есть пару оптимальных смешенных стратегий и соответствующих для его конкурента .

С начало определим оптимальную смешенную стратегию . Согласно теореме об активных стратегиях, если мы будем придерживаться этой стратегии, то независимо от образа действий противника (если он только не выходит за пределы своих активных стратегий) выигрыш .

В игре 2 X 2 обе стратегии противника являются активными (иначе игра имела седловую точку). Если мы придерживаемся своей оптимальной стратегии , то противник, не меняя выигрыша, может применить любую из своих чистых стратегий:

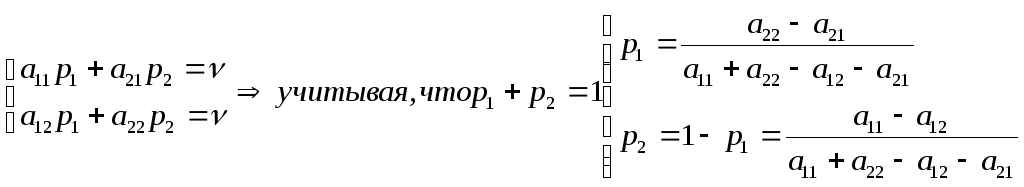
- цена игры, .

Аналогично находится оптимальная стратегия конкурента из уравнения:

.

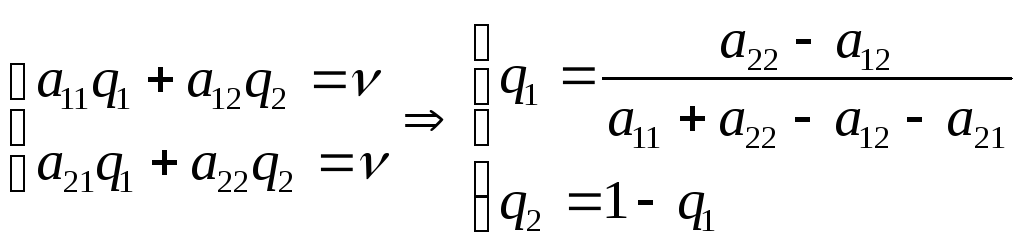4. Геометрическая интерпретация решения игры 2 X 2

Пусть задана матрица игры 2 X 2:

Ai/Bj	B1	B2
A1
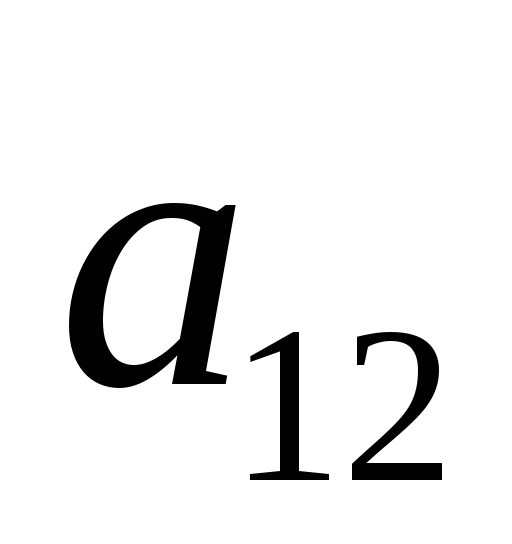
A2

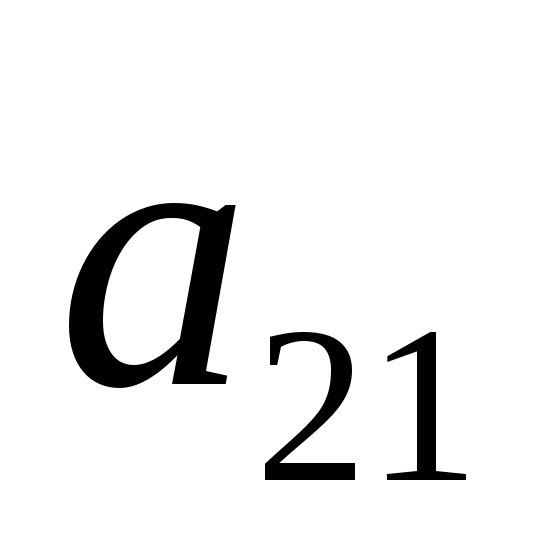
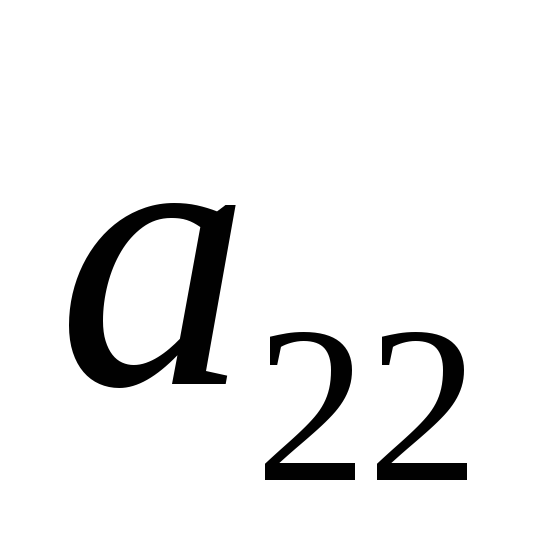
Возьмем участок оси X длинной 1. Левый конец участка (точка X=0) будет изображать стратегию A1. Правый конец участка (точка X=1) будет изображать стратегию A2. Все промежуточные точки участка будут изображать смешенные стратегии игрока A. Причем вероятность p1 стратегии A1 будет равна расстоянию от точки до правого конца участка. А вероятность p2 стратегии A2 - расстоянию до левого конца.

Проведем через точки A1 и A2 два перпендикуляра к оси X: 1-1 и 2-2.

На оси 1-1 будем откладывать выигрыши при стратегии A1, а на оси 2-2 выигрыш при стратегии A2. Пусть противник принимает стратегию B1, она дает на осях 1-1 и 2-2 соответственно точки с ординатами и . Проведем через эти точки прямую B1B1. Очевидно, при любой смешенной стратегии наш выигрыш выразится точкой М на прямой B1B1 соответствующей точке на оси X, делящая отрезок в соотношение p2p1.

Очевидно, также может быть построена прямая для стратегии B2. Нам необходимо найти оптимальную стратегию , то есть такую, при которой наш минимальный выигрыш (при наилучшем для нас поведении B) обращался бы в максимальный. Для этого построим границу выигрыша при стратегиях B1 и B2, то есть ломанную B1NB2.

Н

N

B2

B1

а этой границе будет лежать минимальный выигрыш игрока A, при любой его смешенной стратегии. Точка N в которой этот выигрыш достигает максимума, определяет решение и цену игры. Ордината точки N – есть цена игры . Значения P1 и P2 определяют стратегию .

1

2

B1

B2

1

2

S*

Однако точка пересечения не всегда определяет решение игры. Решение игр больше размерности требуют применение специальных методов (итерациональных процедур), однако в некоторых случаях удается упростить многомерную игру с помощью специальных алгоритмов и свести ее к игре любой размерности.

43