- •I. Пределы
- •1.1. Понятие о пределе числовой последовательности.
- •1.2.Правила вычисления пределов последовательностей.
- •1.3. Число е.
- •1.4. Предел функции.
- •1.5. Правила вычисления пределов функции.
- •Раскрытие неопределенностей вида и .
- •1.7. Раскрытие неопределенности вида .
- •1.8. Два замечательных предела.
- •1.9. Сравнение бесконечно малых.
- •II. Дифференцирование.
- •Понятие производной.
- •Вычисление производных.
- •Дифференциал функции.
- •Производные и дифференциалы высших порядков.
- •2.5. Производная неявной функции и параметрически заданной функции.
- •Исследование функций и построение графиков.
- •Основные положения исследования функции.
- •Глава 1.
- •Глава 2.
- •Глава 3.
2.5. Производная неявной функции и параметрически заданной функции.
Для нахождения
производной функции y,
заданной неявно, т.е. уравнением
![]() ,
нужно продифференцировать обе части
уравнения, рассматривая y
как функцию от x,
а затем из полученного уравнения найти
,
нужно продифференцировать обе части
уравнения, рассматривая y
как функцию от x,
а затем из полученного уравнения найти
![]() .
.
Пример 2.10.
Найти
![]() и найти её значение в точке
и найти её значение в точке
![]() ,
если
,
если
![]() .
.
Решение.
Дифференцируем
уравнение:
![]() .
.
В параметрически
заданной функции зависимость y
от x
выражена через параметр t:
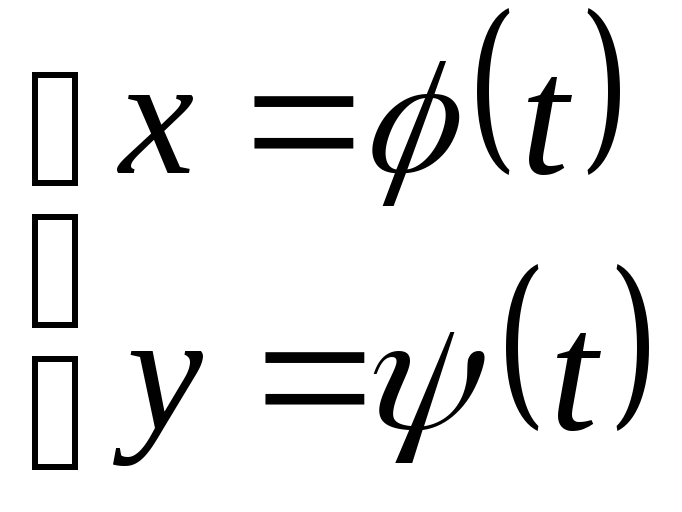 ,
,
![]() .
Производная такой функции находится
по правилу:
.
Производная такой функции находится
по правилу:
![]()
![]() .
.
Производная
второго порядка может быть найдена по
формуле:
![]() .
.
Но можно найти
вторую производную и так:
![]() .
Подобным образом можно получить формулы
для производных
.
Подобным образом можно получить формулы
для производных
![]() по x
порядка
по x
порядка
![]() через производные от x
и y
по t
:
через производные от x
и y
по t
:
![]()
![]() и т.д.
и т.д.
Пример 2.11.
Найти
![]() для
для
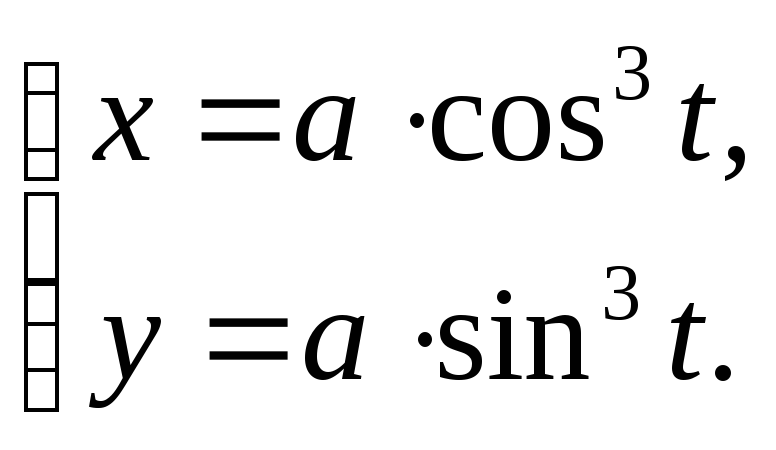
Решение.
Найдем
![]() ,
затем
,
затем
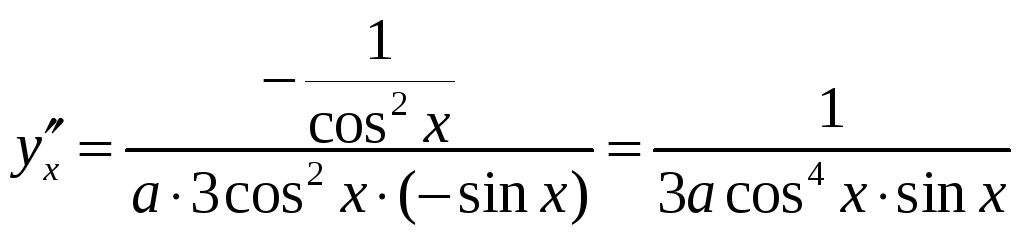 .
.
![]() =
=![]() .
.
-Пуаро,- сказал я. – Я только что думал…
- Очаровательное занятие, мой друг. Не
гнушайтесь им и впредь.
А.Кристи. Загадка Эндхауза.
☼ Упражнения 2.8. Найти производные первого и второго порядков для функций:
1)
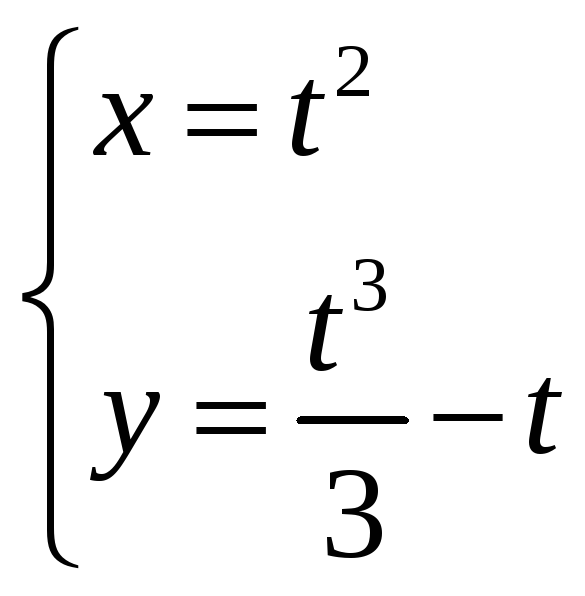 ; 2)
; 2)
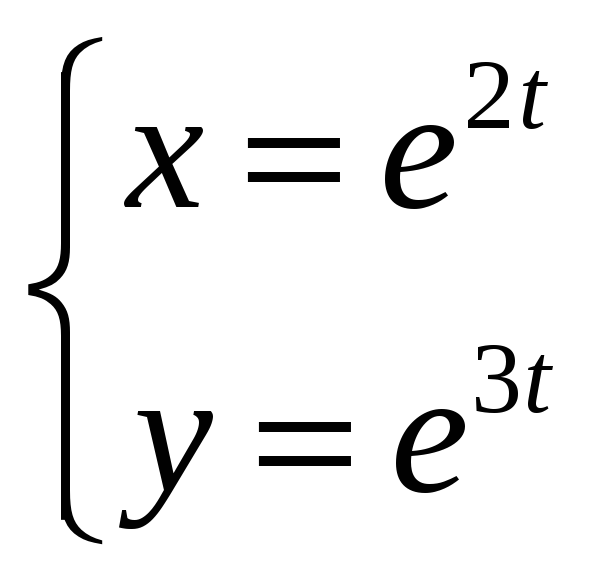 ;
3)
;
3)
![]() ;
4)
;
4)
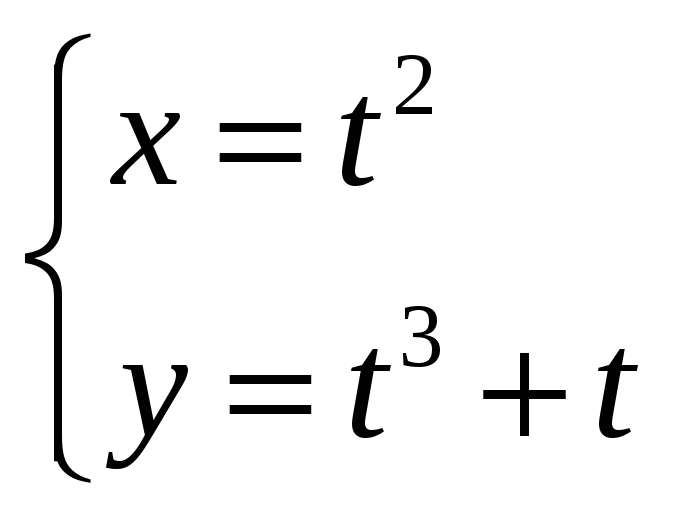 ;
;
5)
![]() ;
6)
;
6)
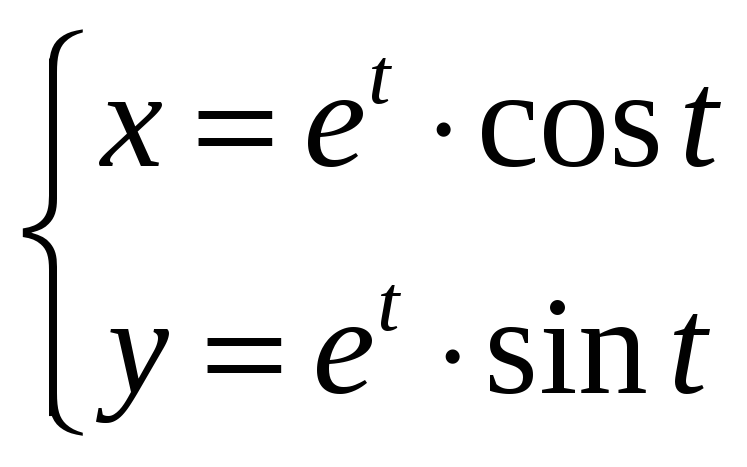 ;
7)
;
7)
![]() ;
8)
;
8)
![]() .
☼
.
☼
-
Исследование функций и построение графиков.
-
Основные положения исследования функции.
С помощью
производной 1-го порядка можно находить
промежутки монотонности функции и точки
ее экстремумов. Если
![]()
![]() ,
то функция
,
то функция
![]() возрастает на
возрастает на
![]() .
Если
.
Если
![]()
![]() ,
то функция
,
то функция
![]() убывает на
убывает на
![]() (рис.1).
(рис.1).
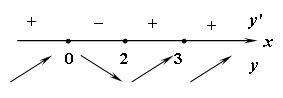 Рис.1.
Рис.1.
Если функция
![]() непрерывна в точке
непрерывна в точке
![]() и производная
и производная
![]() при переходе через точку
при переходе через точку
![]() слева направо меняет знак с «+» на с «-»
(с «-» на с «+»), то
слева направо меняет знак с «+» на с «-»
(с «-» на с «+»), то
![]() является точкой максимума
(минимума),
а значение
является точкой максимума
(минимума),
а значение
![]() - максимумом
(минимумом)
функции
- максимумом
(минимумом)
функции
![]() (рис.2). В обоих случаях точка
(рис.2). В обоих случаях точка
![]() называется точкой экстремума, а значение
называется точкой экстремума, а значение
![]() - экстремумом
функции
- экстремумом
функции
![]() (рис.2)
(рис.2)
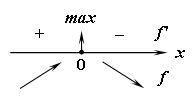 Рис.2.
Рис.2.
С помощью
производной второго порядка находятся
промежутки выпуклости, вогнутости и
точки перегиба графика функции. Если
![]() (<0)
(<0)
![]() ,
то
,
то
![]() возрастает (убывает) на
возрастает (убывает) на
![]() ,
угловой коэффициент к графику функции
,
угловой коэффициент к графику функции
![]() увеличивается (уменьшается)и график
является вогнутым
(выпуклым)
на
увеличивается (уменьшается)и график
является вогнутым
(выпуклым)
на
![]() (рис.3). Точка, в которой вторая производная
меняет знак, называется точкой перегиба
функции
(рис.3). Точка, в которой вторая производная
меняет знак, называется точкой перегиба
функции
![]() .
.
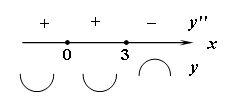 Рис.3.
Рис.3.
Для построения
графика функции полезно найти асимптоты.
Прямая
![]() является вертикальной
асимптотой
графика непрерывной функции
является вертикальной
асимптотой
графика непрерывной функции
![]() ,
если хотя бы один из односторонних
пределов в точке a
равен бесконечности:
,
если хотя бы один из односторонних
пределов в точке a
равен бесконечности:
![]() или
или
![]() .
Асимптота
называется
горизонтальной,
если
.
Асимптота
называется
горизонтальной,
если
![]() .
Прямая
.
Прямая
![]() является наклонной
асимптотой
непрерывной кривой
является наклонной
асимптотой
непрерывной кривой
![]() ,
,
![]() ,
,
![]() .
.
-
Схема построения графика функции.
Чтобы не попасть в капкан,
чтобы в темноте не заблудиться,
чтобы никогда в пути не сбиться,
чтобы в нужном месте приземлиться,
приводниться,-
начерти на карте план.
Если даже есть талант-
чтобы не нарушить, не расстроить
чтобы не разрушить, а построить,
чтобы увеличиться, удвоиться, утроиться
нужен очень точный план.
В. Высоцкий. Песня Алисы о планах.
-
Найти область D значений x, где функция
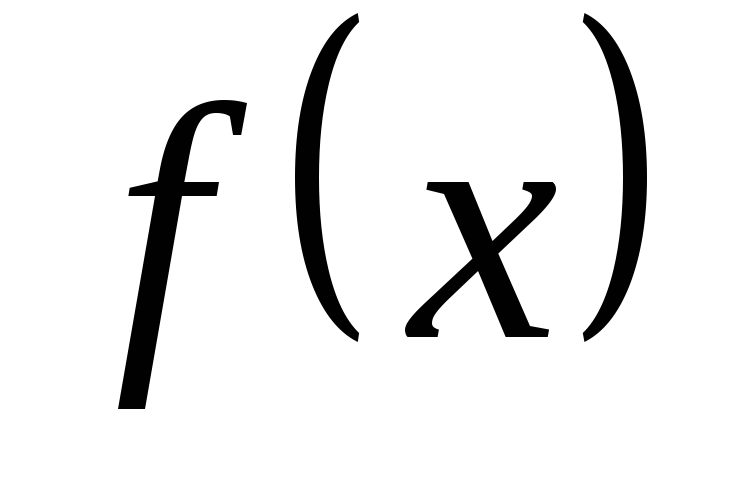 определена.
определена. -
Найти точки
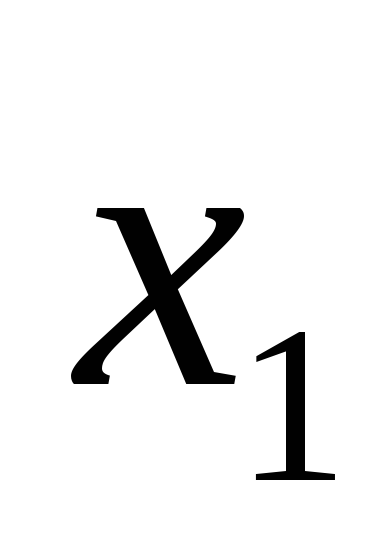 ,
,
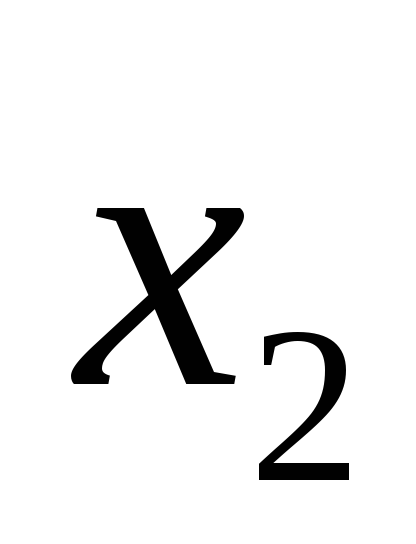 ,
,
 ,
где
,
где
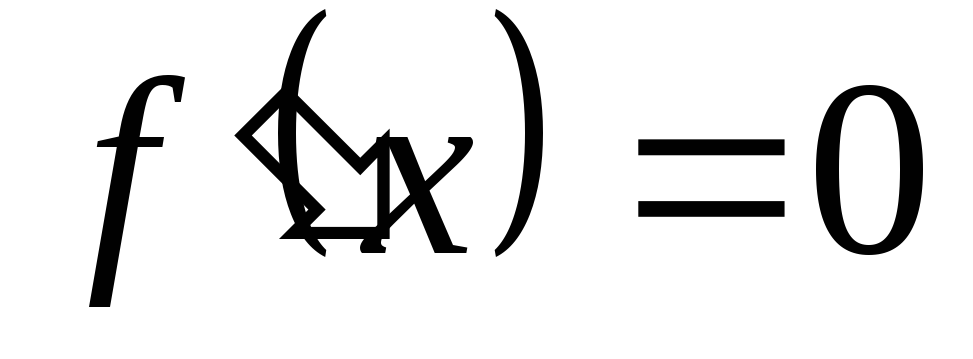 или производная не существует,
или производная не существует,
в частности
равна
![]() .
Вычислить значения
.
Вычислить значения
![]() в этих точках:
в этих точках:
![]() ,
,
![]() ,
,
![]() ,
если они существуют, и определить, не
являются ли они точками максимума или
минимума. Если
,
если они существуют, и определить, не
являются ли они точками максимума или
минимума. Если
![]() не определена в какой-либо из точек
не определена в какой-либо из точек
![]() ,
то важно знать пределы
,
то важно знать пределы
![]() ,
,
![]() ,
а также
,
а также
![]() ,
,
![]() ,
если они имеют смысл.
,
если они имеют смысл.
-
Область D разделяется точками
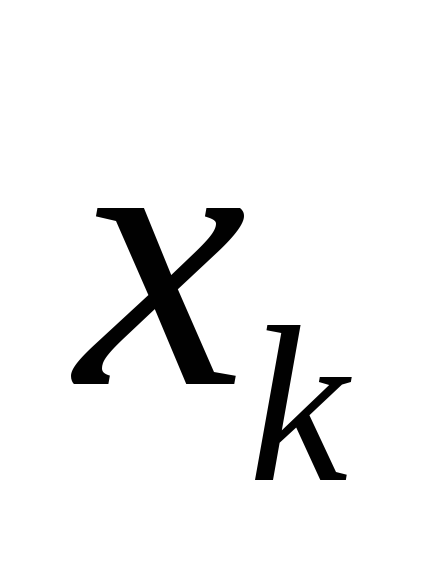 на интервалы
на интервалы
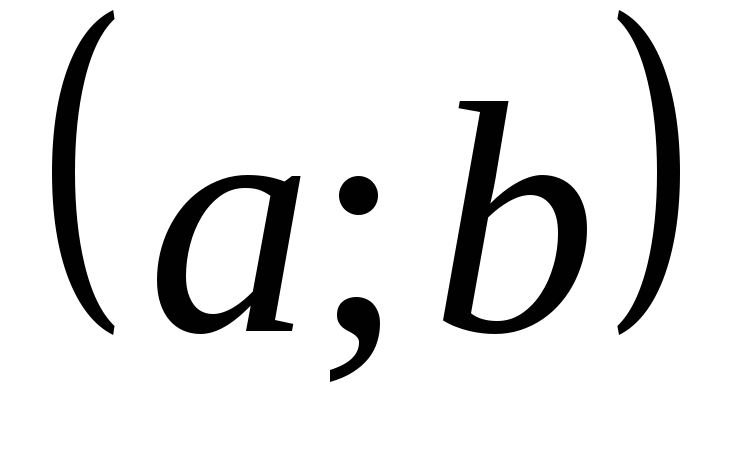 ,
на каждом из которых
,
на каждом из которых
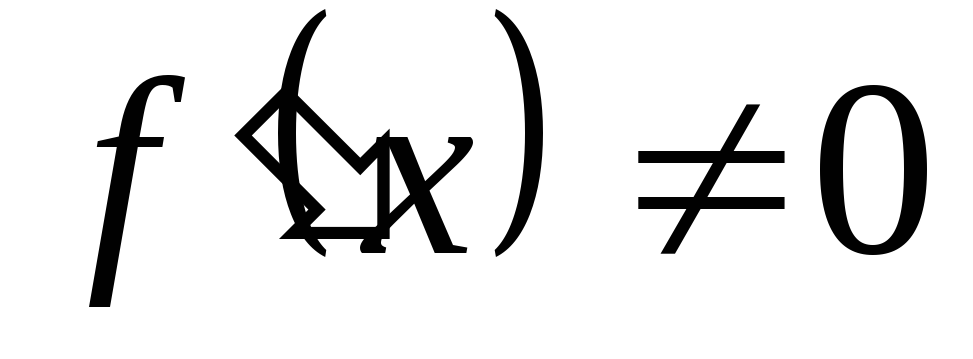 .
Среди них могут быть бесконечные
интервалы вида
.
Среди них могут быть бесконечные
интервалы вида
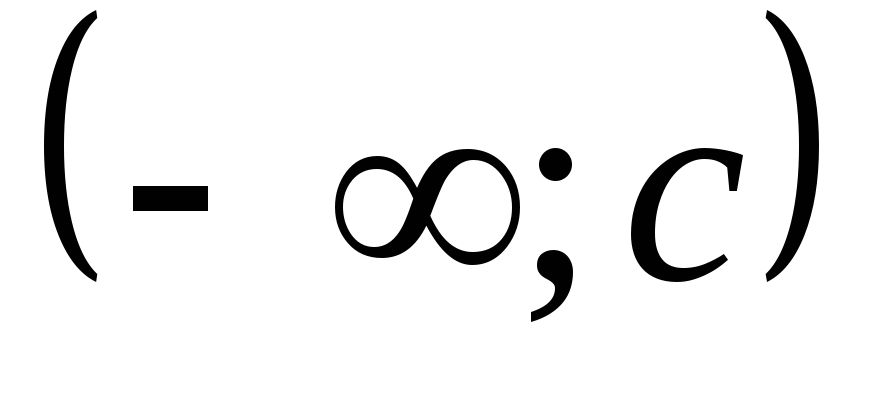 или
или
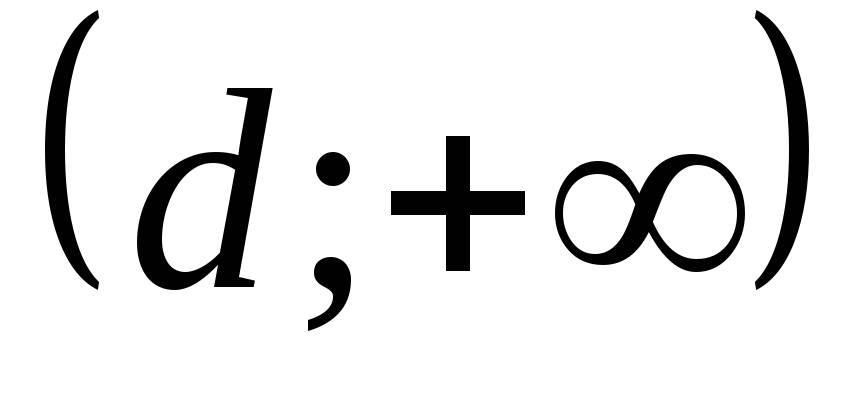 .
Будем считать, что производная
.
Будем считать, что производная
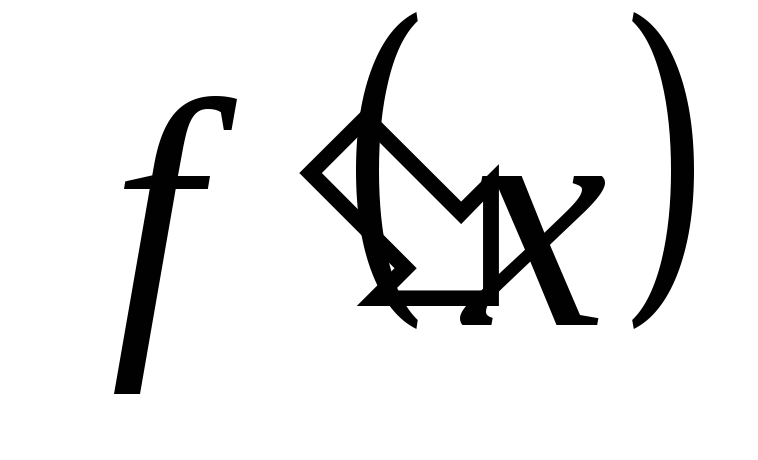 непрерывна на каждом таком интервале
непрерывна на каждом таком интервале
 .
Тогда
.
Тогда
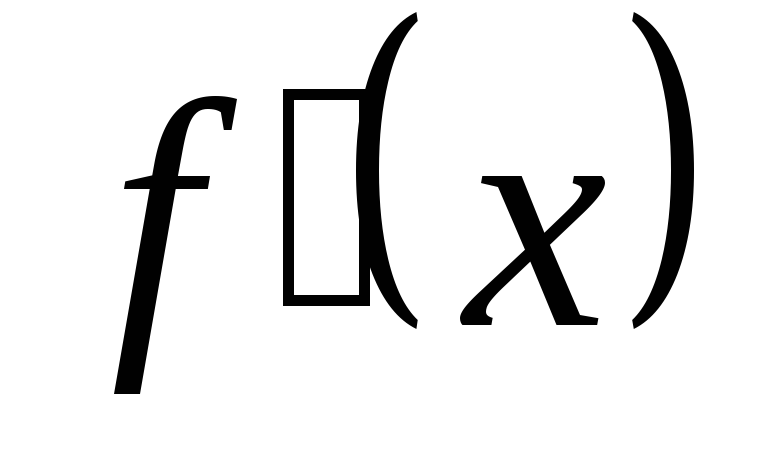 на
на
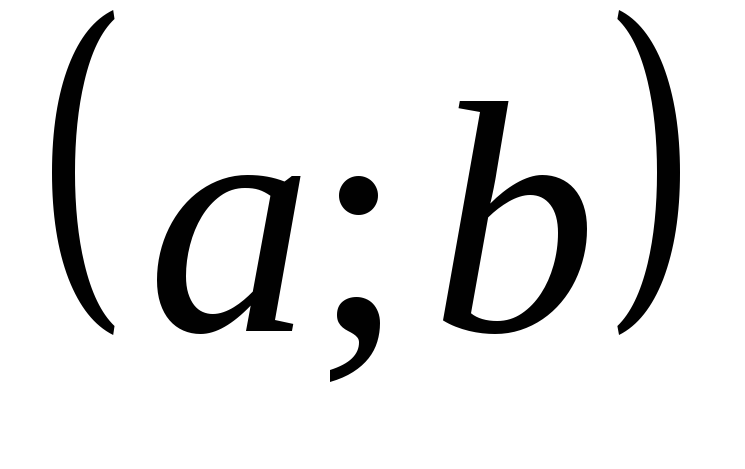 сохраняет знак. Выясним, какой это знак.
Тогда будет известно, возрастает или
убывает функция
сохраняет знак. Выясним, какой это знак.
Тогда будет известно, возрастает или
убывает функция
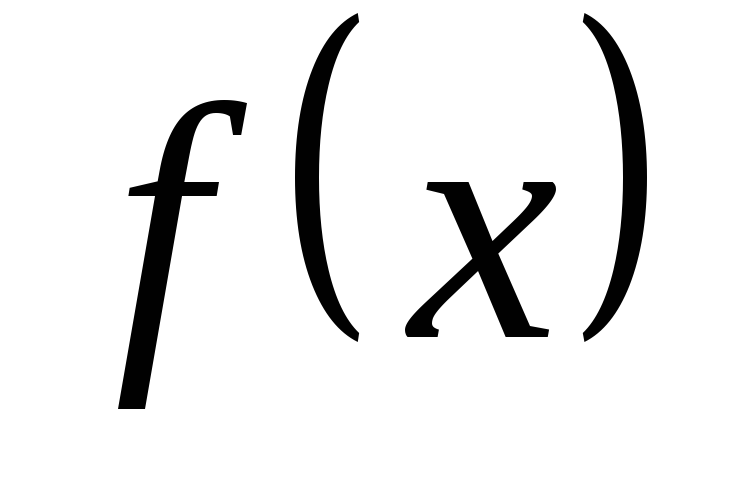 на
на
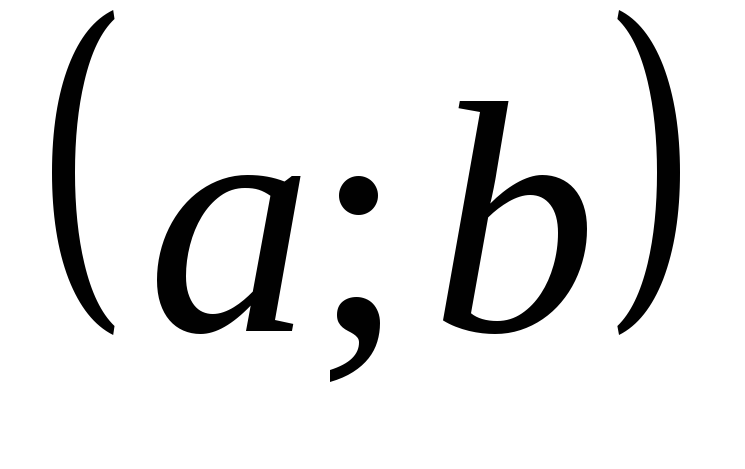 .
. -
Важно отметить на каждом интервале
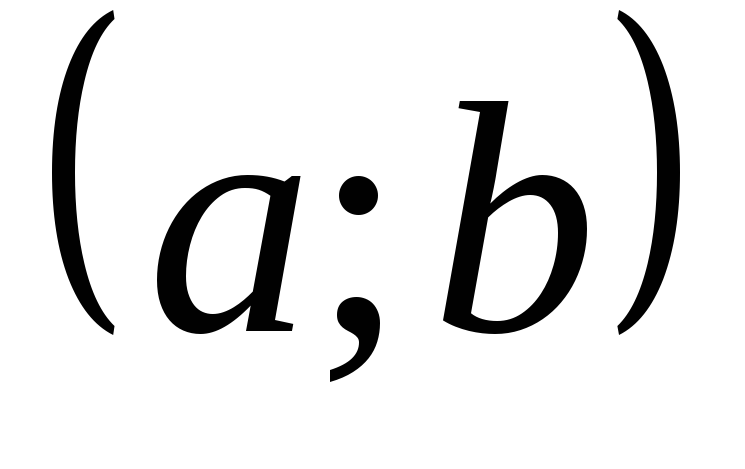 точки
точки
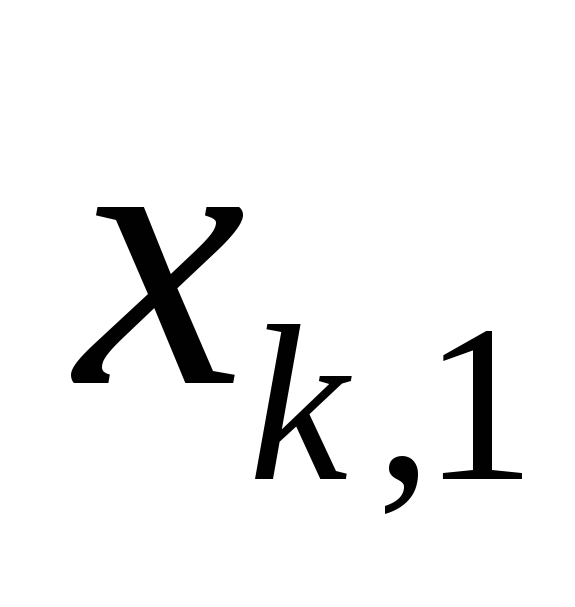 ,
,
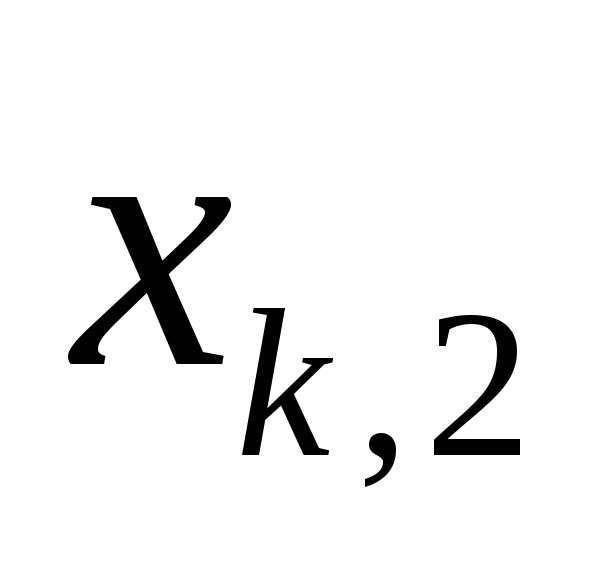 ,
,
 ,
где
,
где
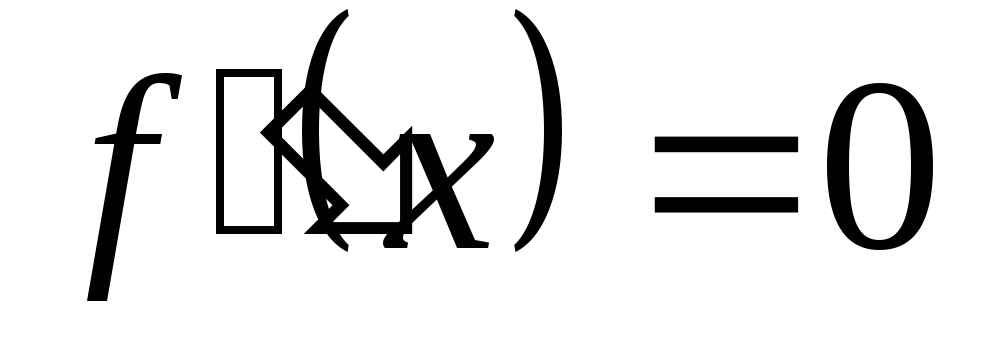 ,
и определить соответствующие значения
функции
,
и определить соответствующие значения
функции
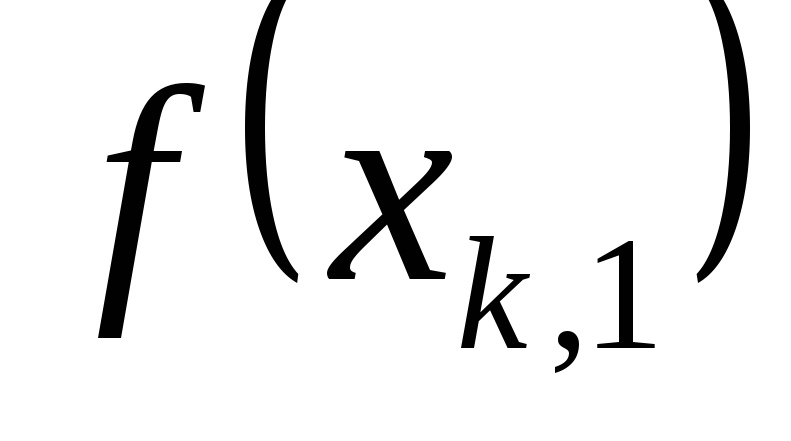 ,
,
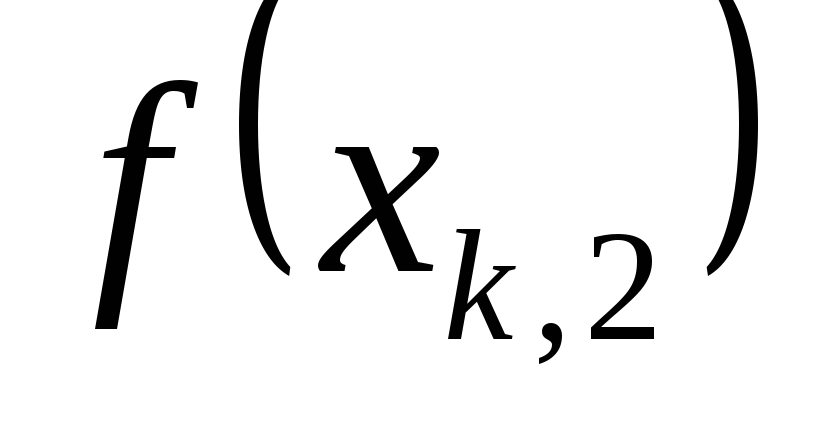 ,
,
 .
В этих точках могут быть точки перегиба
кривой
.
В этих точках могут быть точки перегиба
кривой
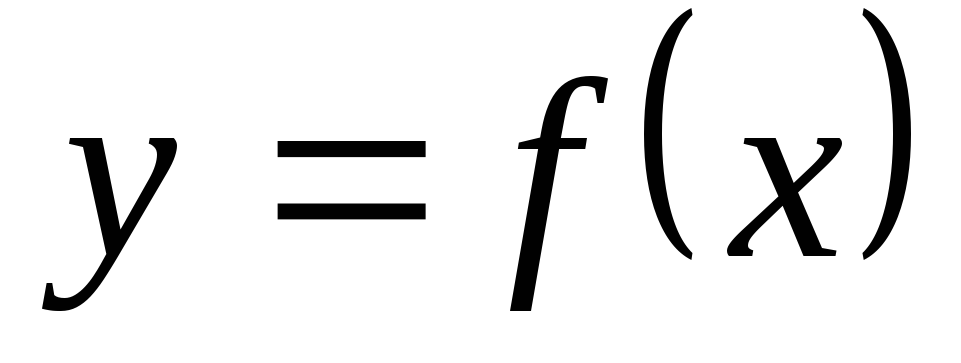 .
Эти точки делят
.
Эти точки делят
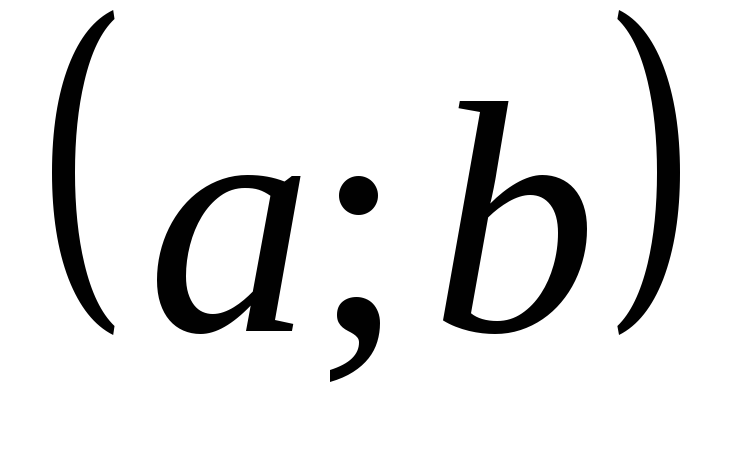 на интервалы, на которых вторая
производная
на интервалы, на которых вторая
производная
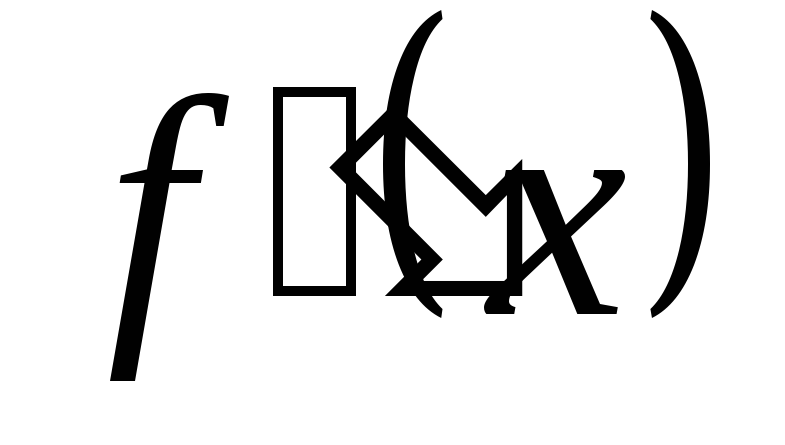 ,
если она существует, сохраняет знак.
Выяснение знака
,
если она существует, сохраняет знак.
Выяснение знака
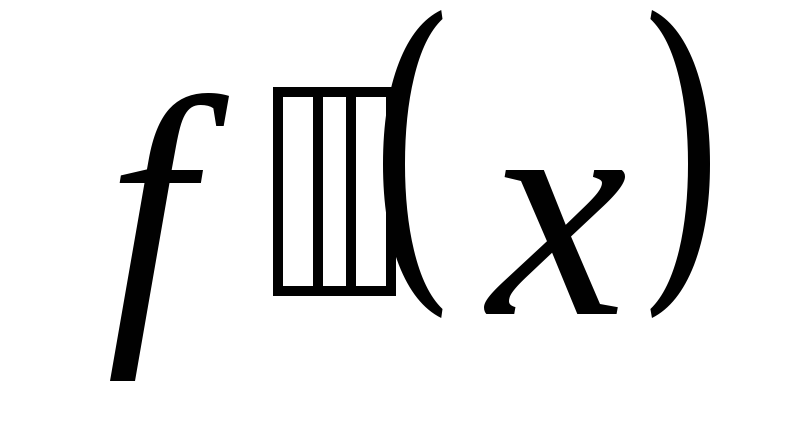 даёт возможность узнать направление
выпуклости кривой.
даёт возможность узнать направление
выпуклости кривой. -
По возможности решить уравнение
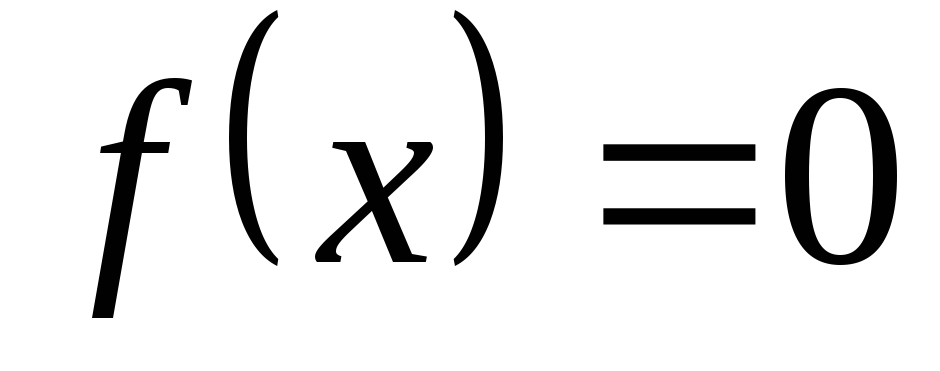 и выяснить интервалы, на которых
и выяснить интервалы, на которых
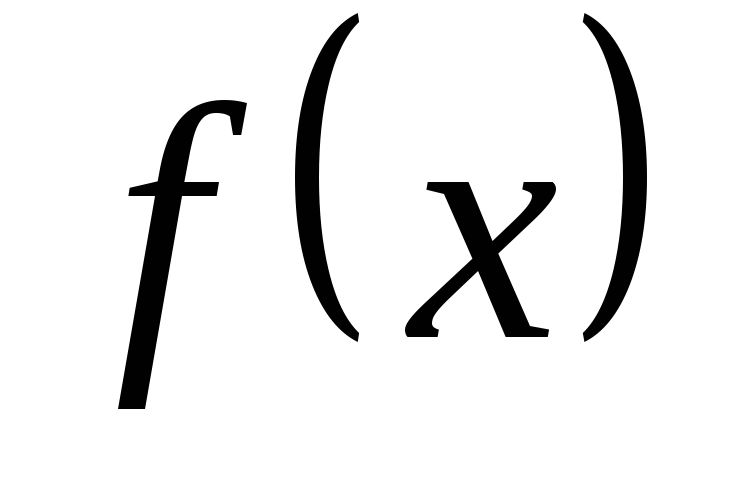 сохраняет знак (
сохраняет знак (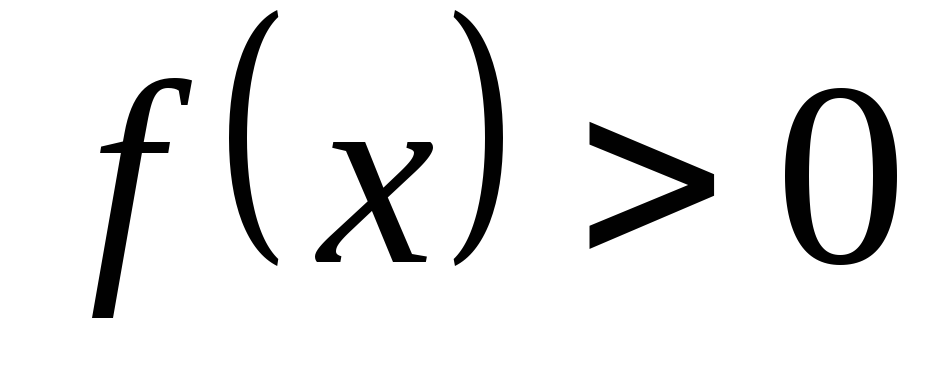 ,
,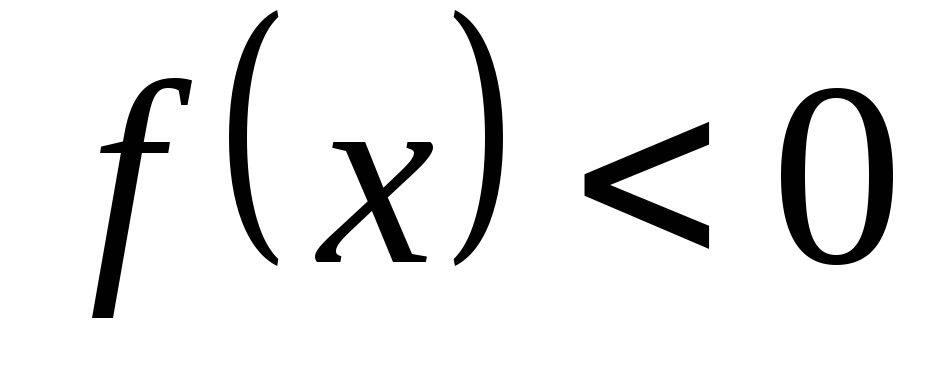 ).
). -
Выяснить вопрос о существовании асимптот, то есть найти пределы
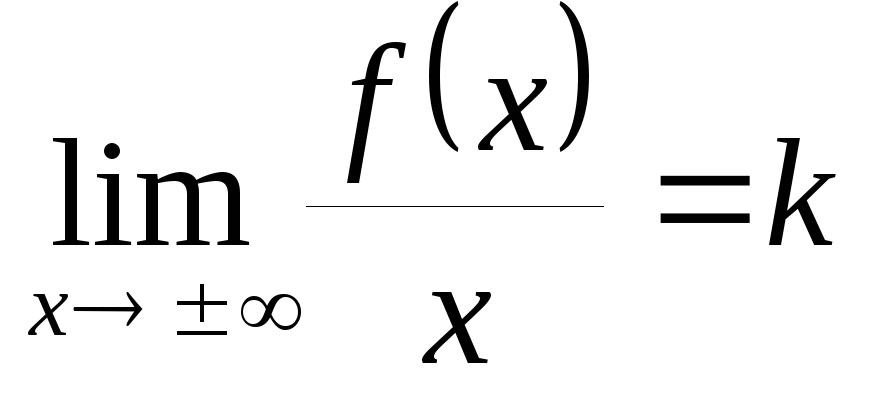 ,
,
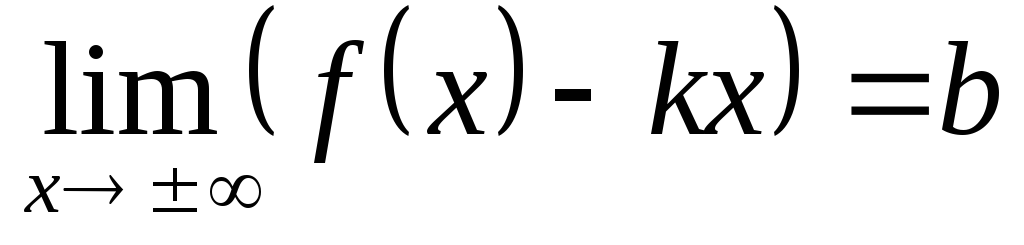 .
. -
На основе сведений построить график функции
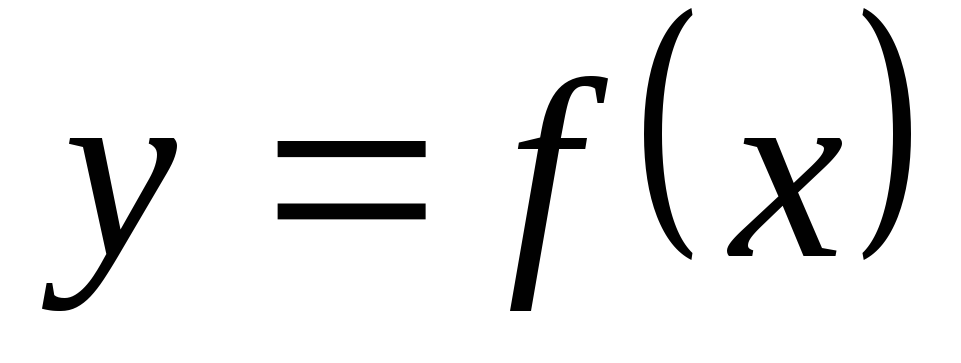 .
.
Пример 3.1.
Исследовать функцию
![]() и построить её график.
и построить её график.
-
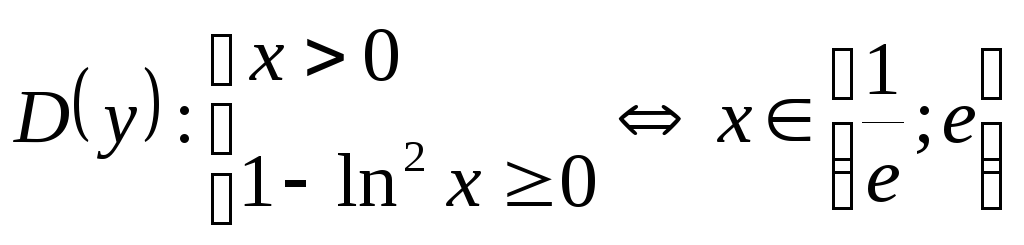 .
. -
Функция общего вида.
-
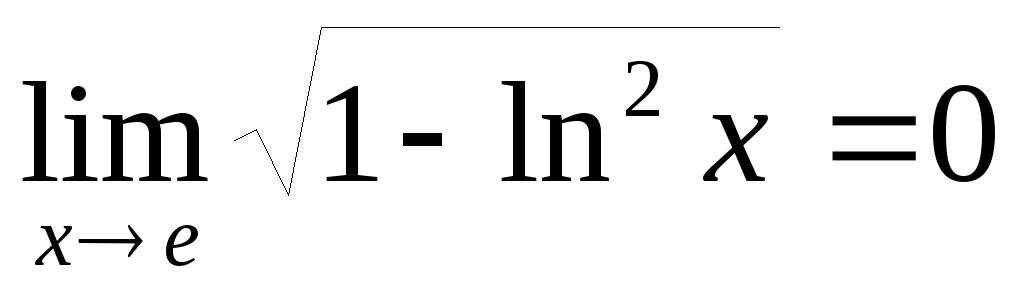 ,
,
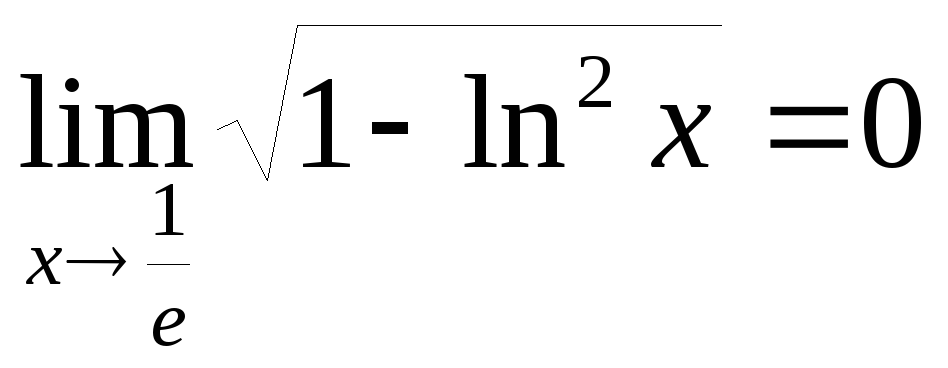 ,
поэтому вертикальных асимптот нет.
,
поэтому вертикальных асимптот нет. -
Так как функция не определена при
 и
и
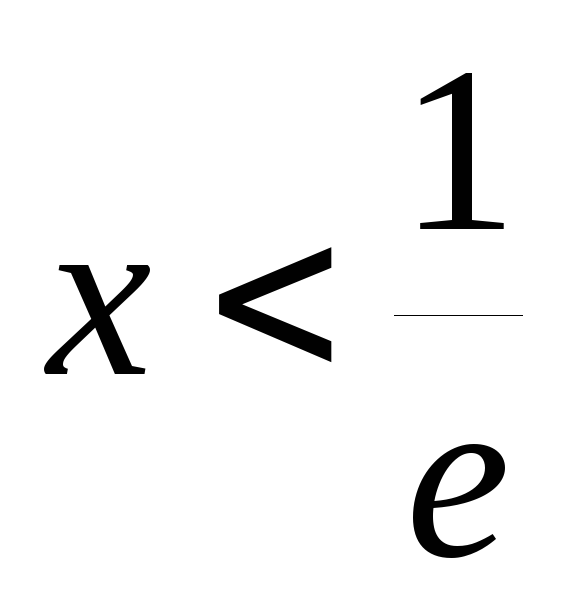 ,
понятие горизонтальной или наклонной
асимптоты для неё не имеет смысла.
,
понятие горизонтальной или наклонной
асимптоты для неё не имеет смысла.
|
|
-
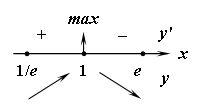
Точки перегиба и интервалы выпуклости:
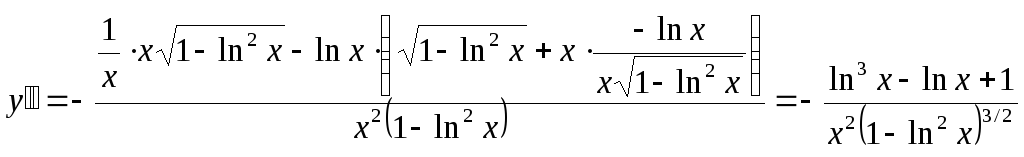 ,
,
![]() ,
поэтому
,
поэтому
![]() и функция выпукла вверх на отрезке
и функция выпукла вверх на отрезке
![]() .
Точек перегиба нет.
.
Точек перегиба нет.
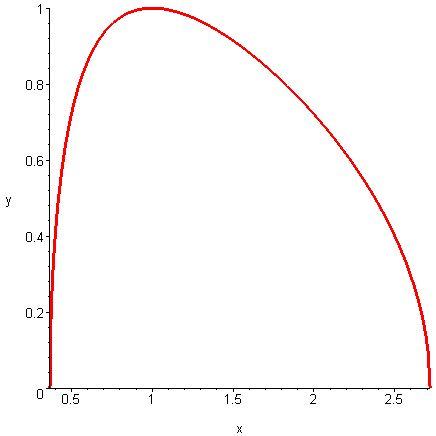
График функции представлен на рис. 4.
|
|
|
|
Рис. 4. |
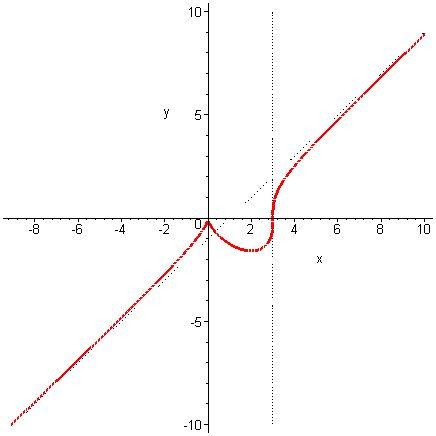
Рис. 5. |
Пример 3.2.
Исследовать функцию
![]() и построить её график.
и построить её график.
-
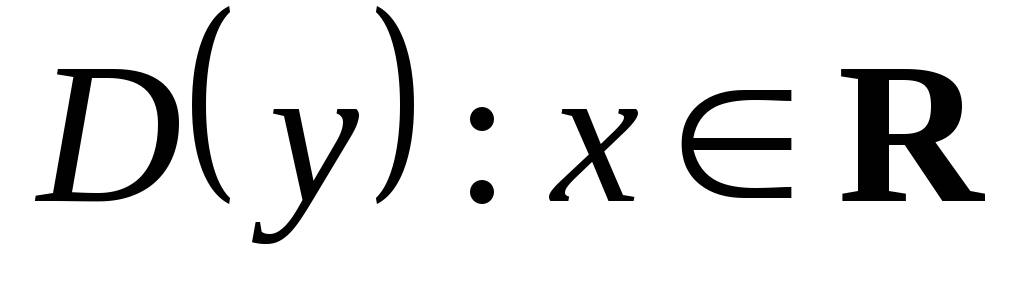 .
. -
Функция общего вида.
-
Вертикальных асимптот нет.
-
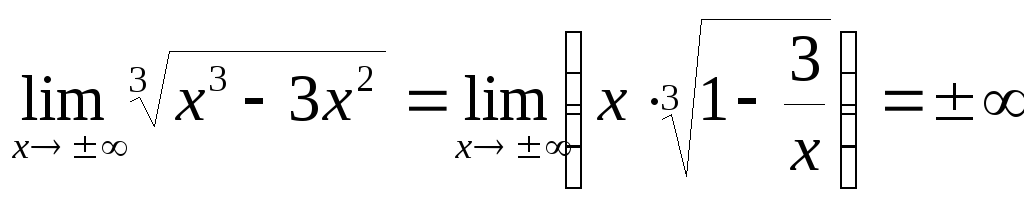 ,
поэтому горизонтальных асимптот нет.
,
поэтому горизонтальных асимптот нет.
Есть ли наклонные
асимптоты?
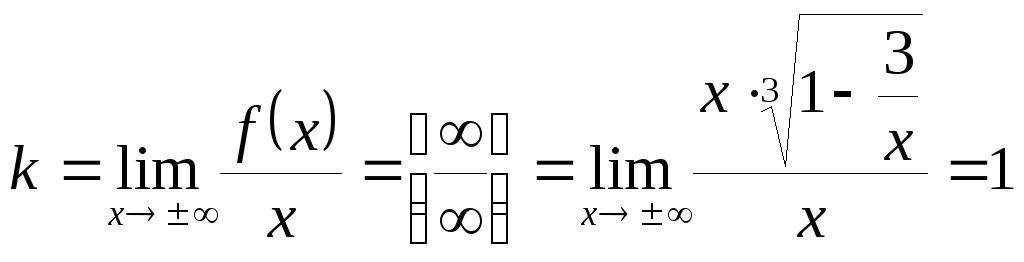 ,
,
![]()
![]() – наклонная
асимптота.
– наклонная
асимптота.
|
|
![]() – точка локального
максимума,
– точка локального
максимума,
![]() ;
;
![]() – точка локального минимума,
– точка локального минимума,
![]() .
.
-
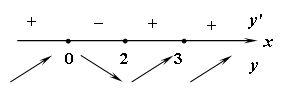
Точки перегиба и интервалы выпуклости:
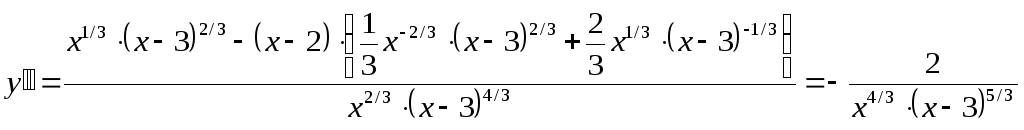 ,
,
|
|
|
-
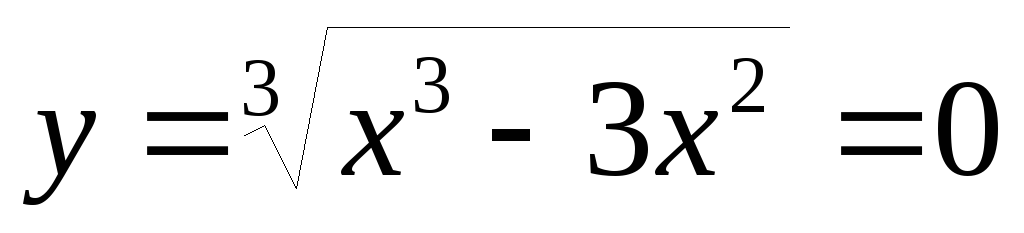 при
при
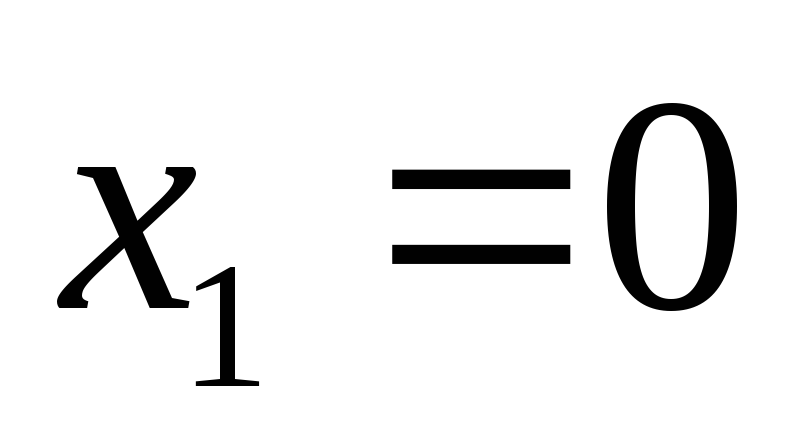 и
и
 .
.
График функции представлен на рис. 5.
- Задай еще вопрос. Какое же наслаждение
наблюдать за работой собственной головы,
решающей мировые проблемы!
Р. Бах. Иллюзии
☼ Упражнения 3.1. Построить графики функций:
1)
![]() ;
2)
;
2)![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() ;
;
6)
![]() ;
7)
;
7)
![]() ;
8)
;
8)
![]() ;
9)
;
9)
![]() ;
10)
;
10)
![]()
11)
![]() ;
12)
;
12)
![]() ;
13)
;
13)
![]() ;
14)
;
14)
![]() ;
15)
;
15)
![]() ;
16)
;
16)
![]() ;
17)
;
17)
![]() ;
18)
;
18)
![]() ;
19)
;
19)
![]() ;
20)
;
20)
![]() ;
21)
;
21)
![]() ;
;
22)
![]() ;
23)
;
23)
![]() ;
24)
;
24)
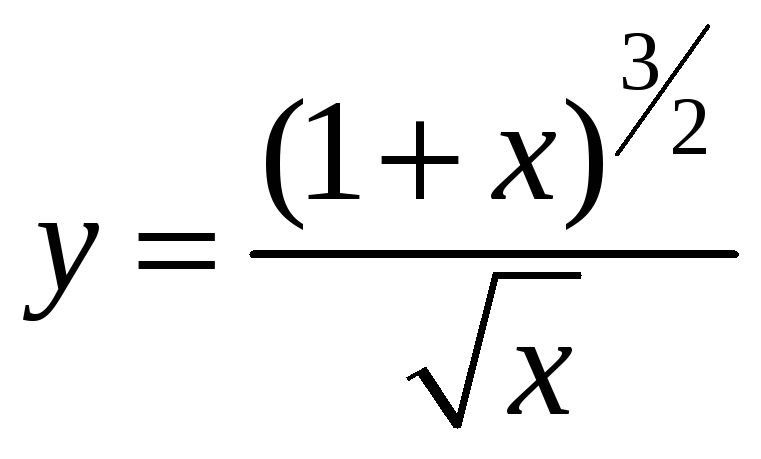 ;
25)
;
25)
![]() ;
;
26)
![]() ;
27)
;
27)
![]() .
☼
.
☼
Я просил его присутствовать, ибо сегодня он
услышит ответы на свои вопросы.
Дж.Р.Р. Толкин. «Властелин Колец».
Ответы, указания.