
- •I. Пределы
- •1.1. Понятие о пределе числовой последовательности.
- •1.2.Правила вычисления пределов последовательностей.
- •1.3. Число е.
- •1.4. Предел функции.
- •1.5. Правила вычисления пределов функции.
- •Раскрытие неопределенностей вида и .
- •1.7. Раскрытие неопределенности вида .
- •1.8. Два замечательных предела.
- •1.9. Сравнение бесконечно малых.
- •II. Дифференцирование.
- •Понятие производной.
- •Вычисление производных.
- •Дифференциал функции.
- •Производные и дифференциалы высших порядков.
- •2.5. Производная неявной функции и параметрически заданной функции.
- •Исследование функций и построение графиков.
- •Основные положения исследования функции.
- •Глава 1.
- •Глава 2.
- •Глава 3.
1.3. Число е.
Последовательность
![]() монотонная и ограниченная. Следовательно,
она имеет конечный предел. Этот предел
определяет эйлерово число
монотонная и ограниченная. Следовательно,
она имеет конечный предел. Этот предел
определяет эйлерово число
![]() .
Число е – иррациональное, е
.
Число е – иррациональное, е
![]() .
.
Пример 1.7.
Найти
пределы: 1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
Решение.
1)
![]() .
.
2)
![]()
![]() .
.
3)
![]() .
J
.
J
- Надо же как все просто.
- Как научиться ходить. Потом ты начинаешь
удивляться, что в этом было такого сложного.
Р. Бах. Иллюзии
☼ Упражнения 1.2. Вычислить пределы:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ; 5)
; 5)
![]() ;
;
6)
![]() ; 7)
; 7)
![]() ;
8)
;
8)
![]() .
☼
.
☼
1.4. Предел функции.
Пусть функция
f(![]() )
определена на некотором промежутке Х
и пусть точка
)
определена на некотором промежутке Х
и пусть точка
![]() или
или
![]() .
.
Определение 1.2.
Число А
называется пределом функции
![]() (
(![]() )
в точке
)
в точке
![]() ,
если
,
если![]() такое, что для всех
такое, что для всех
![]() ,
,
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() .
.
Записывается так:
![]()
Пример 1.8.
Используя
определение, докажем, что функция
![]() в точке
в точке
![]() имеет предел, равный единице, т.е.
имеет предел, равный единице, т.е.
![]()
Возьмем любое
![]() .
Найдем такое
.
Найдем такое
![]() ,
при котором из неравенства
,
при котором из неравенства
![]() следовало бы неравенство
следовало бы неравенство
![]() .
Преобразуя неравенство, получаем
.
Преобразуя неравенство, получаем
![]() .
Отсюда видно, что если взять
.
Отсюда видно, что если взять
![]() ,
то для всех
,
то для всех
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]() ,
выполняется требуемое неравенство
,
выполняется требуемое неравенство
![]() .
Это и означает, что
.
Это и означает, что
![]() В частности, если
В частности, если
![]() ,
то
,
то
![]() .
J
.
J
☼ Упражнения 1.3. Используя определение, доказать, что:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
7)
;
7)
![]() ;
8)
;
8)
![]() .
☼
.
☼
1.5. Правила вычисления пределов функции.
Пусть функции
![]() и
и
![]() имеют в точке
имеют в точке
![]() пределы В и A.
Тогда
пределы В и A.
Тогда
1.
![]() =
=
![]() ;
;
2.
![]() ;
3.
;
3.
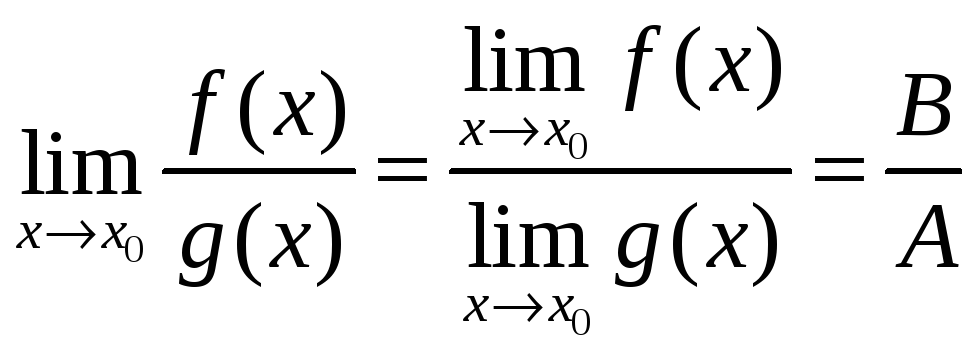 (при
(при
![]() ).
).
4.
![]() ;
5.
;
5.
![]() =
С
=
С![]() B;
B;
Правила верны
также и в случае, когда
![]() является одним из символов
является одним из символов
![]() или
или
![]() .
.
Пример 1.9.
Найти
![]() .
.
Решение.
По правилам вычисления предела функции находим
![]() =
=
![]() .
J
.
J
☼ Упражнения 1.4. Найти пределы:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
7)
;
7)
![]() ;
8)
;
8)
![]() .
☼
.
☼
-
Раскрытие неопределенностей вида и .
Пример 1.10.
Найти
![]() .
.
Решение.
Имеем неопределенность
вида
![]() .
Разложим числитель и знаменатель на
множители и сократим на общий множитель,
который обращает в нуль числитель и
знаменатель дроби:
.
Разложим числитель и знаменатель на
множители и сократим на общий множитель,
который обращает в нуль числитель и
знаменатель дроби:
![]() =
=
![]() .
J
.
J
Пример 1.11.
Найти
![]() .
.
Решение.
Имеем неопределенность
вида
![]() .
Так же, как и в случае последовательностей
заменим бесконечно большие функции на
эквивалентные и найдем предел дроби:
.
Так же, как и в случае последовательностей
заменим бесконечно большие функции на
эквивалентные и найдем предел дроби:
![]()
![]() .
J
.
J
Пример 1.12.
Найти
![]() .
.
Решение.
Имеем неопределенность
вида
![]() .
Заменим бесконечно большие функции на
эквивалентные и найдем предел дроби:
.
Заменим бесконечно большие функции на
эквивалентные и найдем предел дроби:
![]() .
J
.
J
Пример 1.13.
Найти
![]() .
.
Решение.
Имеем неопределенность
вида
![]() .
Заменим бесконечно большие функции на
эквивалентные и найдем предел дроби:
.
Заменим бесконечно большие функции на
эквивалентные и найдем предел дроби:
![]() .
J
.
J
Сопоставляя
результаты решений примеров 1.11 - 1.13
установим правило нахождения пределов
с неопределенностью
![]() .
Если
.
Если
![]() -
многочлены степеней m
и k
соответственно, то
-
многочлены степеней m
и k
соответственно, то
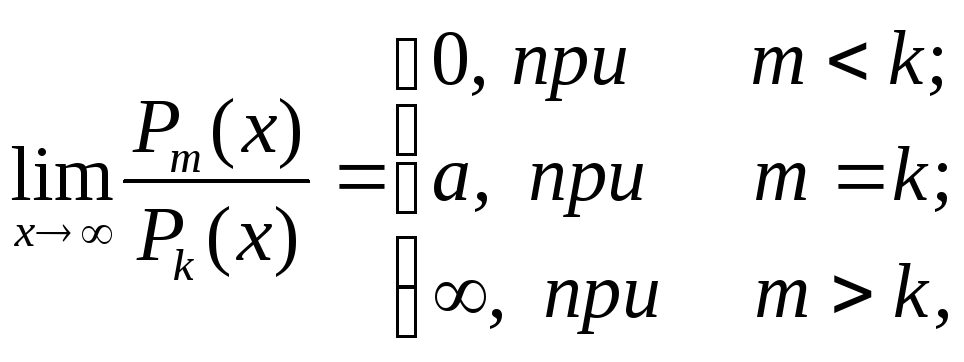
где
![]() - отношение коэффициентов при старших
степенях многочленов.
- отношение коэффициентов при старших
степенях многочленов.
Пример 1.14.
Вычислить
![]() .
.
Решение.
Учитывая условие
![]() ,
получаем
,
получаем
![]()
![]() .
J
.
J
☼ Упражнения 1.5. Найти пределы:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
 ;
;
5)
![]() ;
6)
;
6)
![]() ;
7)
;
7)
![]() ;
;
8)
![]() ;
☼
;
☼
