Закон равномерного распределения вероятностей непрерывной случайной величины

Непрерывная случайная величина Х имеет равномерное распределение вероятностей если ее плотность распределения задается следующим образом:

Найдем значение с. По свойству плотностей распределения получаем

,

следовательно, и

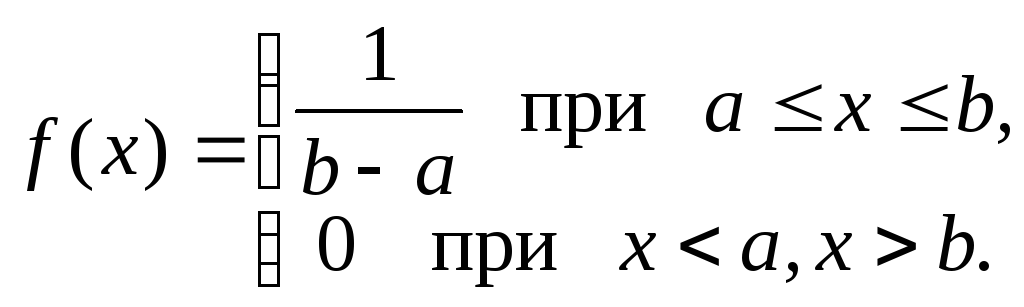
Так как , то промежуток [a, b], на котором имеет место равномерное распределение, обязательно конечен.

Определим вероятность того, что случайная величина Х примет значение, заключенное в интервале (α, β).

.

Итак, искомая вероятность

,

т.е. вероятность попадания Х в интервал зависит только от длины этого интервала и не зависит от значений величины Х. При равномерном распределении случайной величины Х вероятности попадания Х в промежутки равной длины одинаковы.

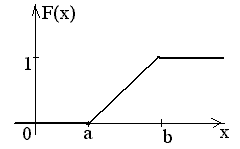
Найдем функцию распределения .

Если х<a, то f(x)=0 и, следовательно, .

Если а≤x≤b, то и, следовательно,

.

Если х>b, то f(x)=0 и, следовательно,

.

Таким образом,

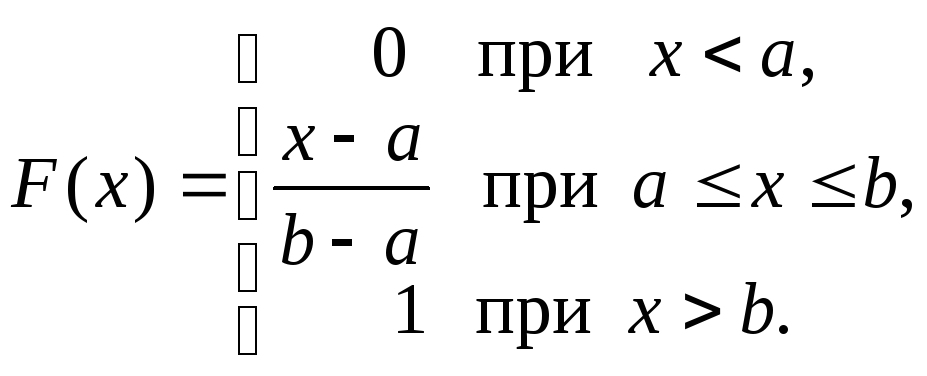
Пример. Интервал движения автобуса равен 20 минутам. Найти вероятность того, что пассажир будет ожидать автобус менее 5 минут.

Пусть случайная величина Х – время прихода пассажира на станцию после отправления очередного автобуса 0<X<20. Х имеет равномерное распределение, так как вероятность прихода, например, в пятую минуту, равна вероятности прихода в восьмую. В задаче требуется найти вероятность того, что случайная величина Х примет значение из интервала (15, 20).

.

Числовые характеристики равномерного распределения

Для случайной величины Х, имеющей равномерное распределение, плотность распределения определяется формулой

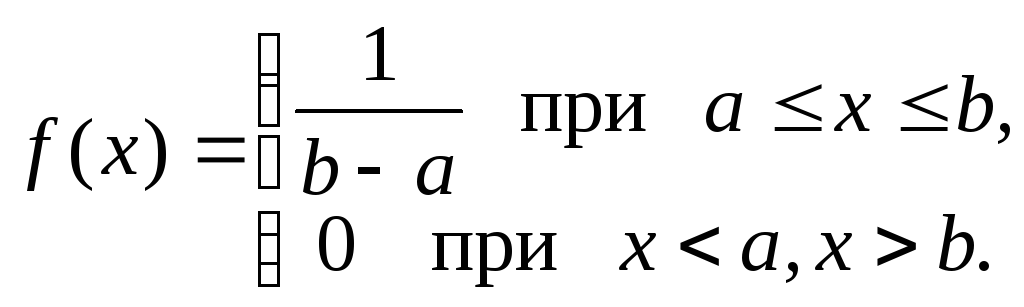
Тогда по определению математического ожидания

.

.

Дисперсия равномерно распределенной случайной величины будет

.

Итак,

, =, .

Нормальный закон распределения непрерывной случайной величины

И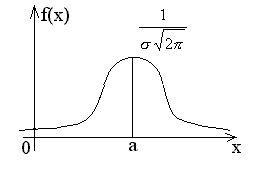зучение различных явлений показывает, многие случайные величины, например, такие, как погрешности при измерениях, величина износа деталей во многих механизмах и т.д., имеет плотность распределения вероятности, которая определяется формулой

,

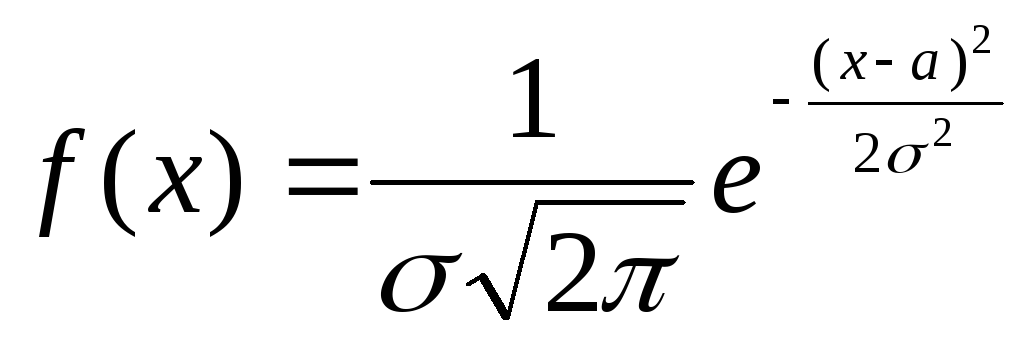где а и σ – параметры распределения. В этом случае говорят, что случайная величина Х подчинена нормальному закону распределения. Кривая нормального распределения изображена на рисунке.

В дальнейшем нам потребуется интеграл Пуассона

.

Используя этот интеграл несложно заметить, что функция распределения f(x) удовлетворяет основному соотношению

.

Действительно, обозначив , можно написать

.

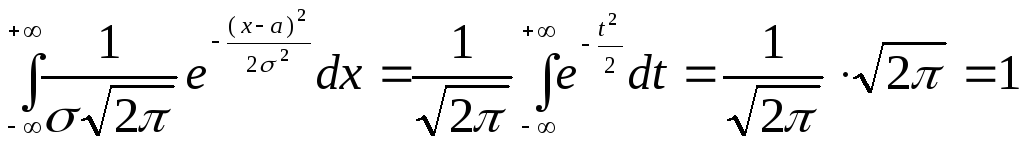Числовые характеристики нормального распределения

Определим математическое ожидание случайной величины с нормальным законом распределения

.

.

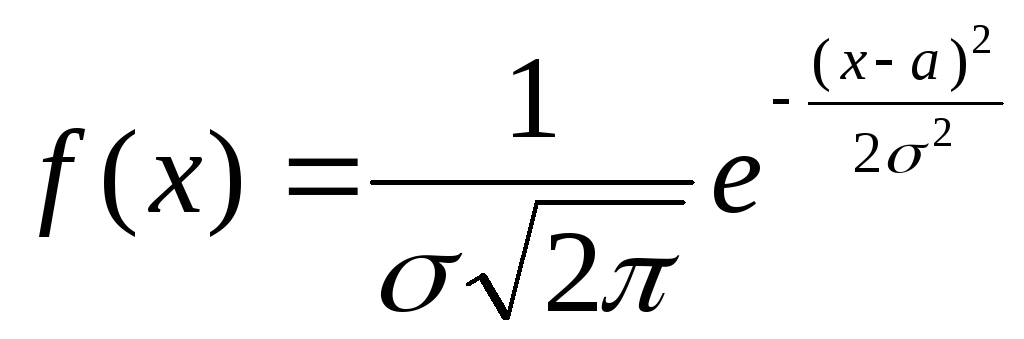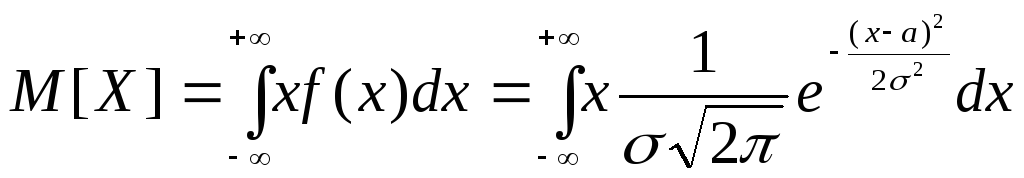Выполнив замену переменной , получаем

.

Итак, М[X]=a. Значение параметра а в формуле, определяющей плотность распределения вероятности, равно математическому ожиданию рассматриваемой случайной величины. Точка х=а является центром распределения вероятностей, или центром рассеивания.

Найдем

.

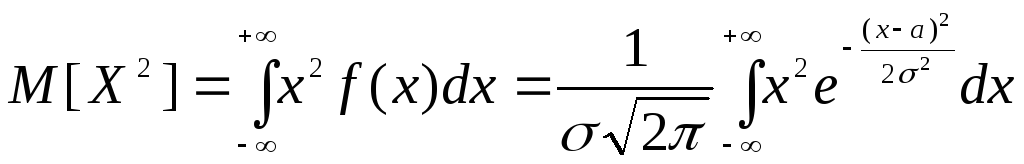Выполнив ту же замену переменной, будем иметь

.

Проинтегрировав по частям последний интеграл: u=t, , получим

.

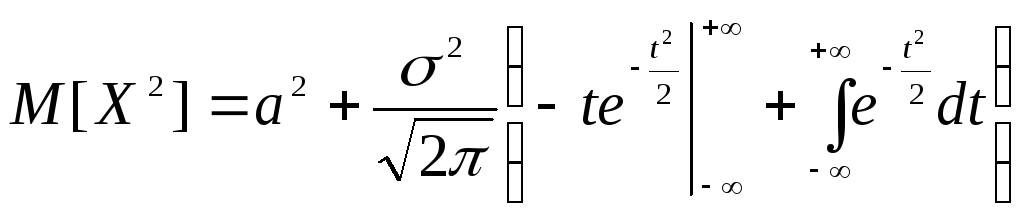Так как по правилу Лопиталя , то

.

Поэтому дисперсия нормального распределения случайной величины будет

.

Итак, M[X]=a, D[X]=σ², σ[X]= σ.