Относительная частота события. Статистическое определение вероятности

Недостатком классического определения вероятности является то, что не всегда удается узнать, являются исходы испытания равновозможными или не являются.

Относительной частотой р^* случайного события А называется отношение числа m^* появления данного события к общему числу n^* проведенных одинаковых испытаний, в каждом из которых могло появиться или не появиться данное событие.

.

Оказывается, что при большом числе испытаний n, относительная частота появления события А в различных сериях отличается друг от друга мало и это отличие тем меньше, чем больше испытаний в сериях.

При статистическом определении вероятностью события называют относительную частоту события при большом числе испытаний или число близкое к ней:

.

Сложение вероятностей

Суммой двух событий А и B называется событие С, состоящее в появлении хотя бы одного из этих событий. Сумма обозначается: С=А+В=АилиВ.

Теорема о сложении вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.

Р(АилиВ)=Р(А)+Р(В).

Заметим, что сформулированная теорема справедлива для любого числа слагаемых:

.

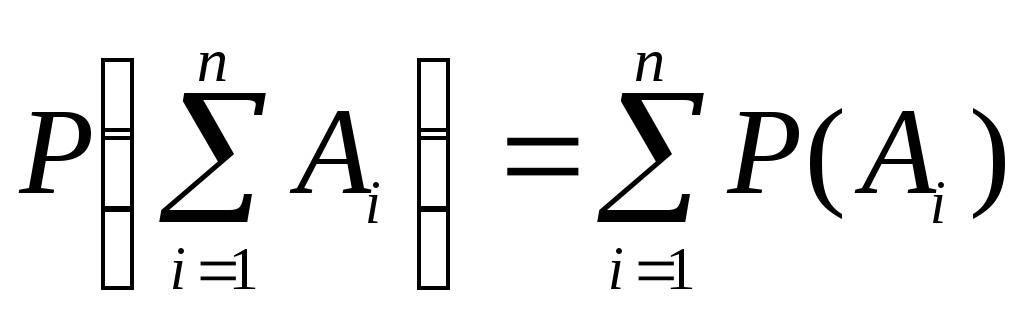Два события называются противоположными, если они несовместны и образуют полную группу. Если событие обозначим через А, то противоположное ему – через .

Так как при испытании обязательно произойдет или событие А или событие , то согласно теореме о сложении вероятностей получаем .

Если случайные события А₁, А₂,…, А_n образуют полную группу несовместных событий, то имеет место равенство

.

Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события. Событие, заключающееся в совмещении событий А и B, будем обозначать АиВ или АВ.

Теорема. Вероятность суммы совместных событий вычисляется по формуле

.

Примеры. 1. В урне 10 белых, 15 черных, 20 синих и 25 красных шаров. Вынули один шар. Найти вероятность того, что вынутый шар а) синий или черный; б) белый, черный или синий.

Обозначим следующие события:

Б – вынули белый шар, ;

Ч – вынули черный шар, ;

С – вынули синий шар, ;

К – вынули красный шар, .

Тогда искомые вероятности будут:

а) .

б)

или .

2. На стеллаже в библиотеке стоит 15 учебников, причем 5 из них в переплете. Библиотекарь берет три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете.

Рассмотрим два способа решения задачи.

Первый способ. Пусть события А – хотя бы один учебник в переплете;

В – один из взятых учебников в переплете, два – без переплета;

С – два в переплете, один без переплета;

D – все три учебника в переплете.

Очевидно, А=В+С+D. Найдем вероятности событий В, С, и D.

, , .

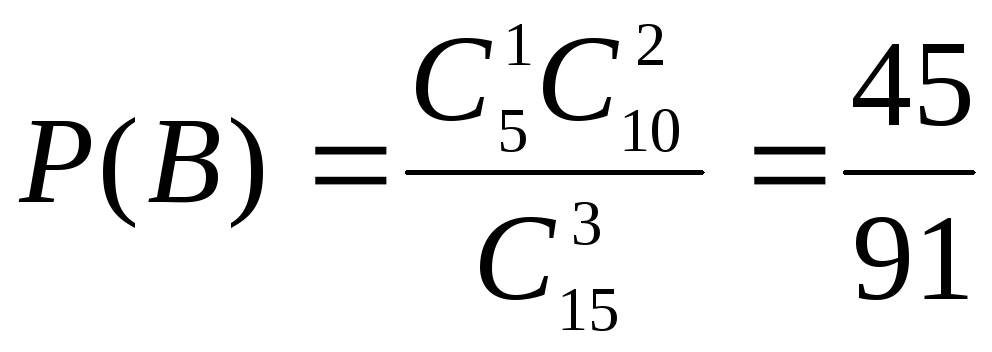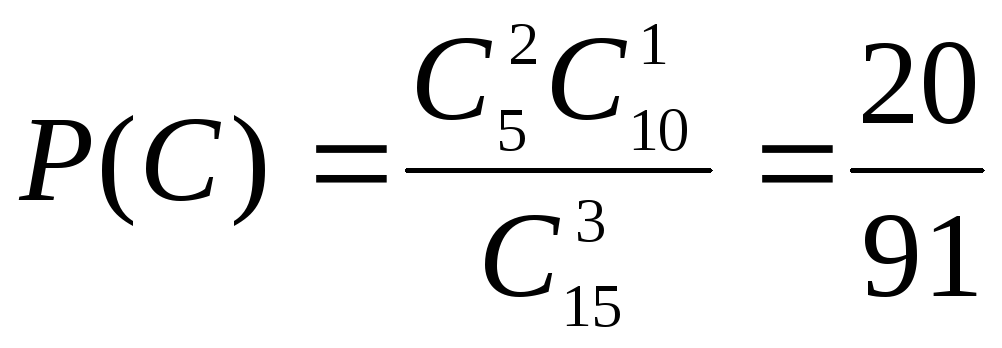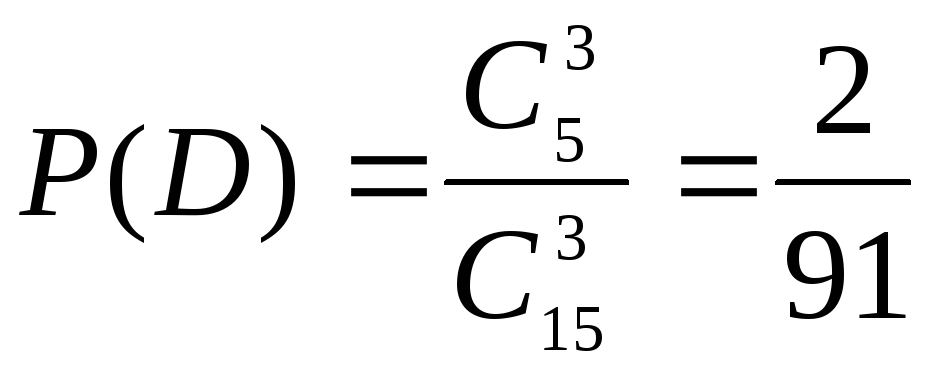Тогда

.

Второй способ. Вновь А – хотя бы один учебник в переплете;

- ни один из взятых учебников не имеет переплета.

Так как события А и противоположные, то

.

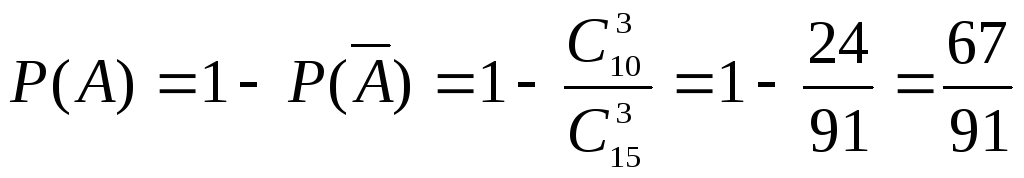Умножение вероятностей независимых событий

Событие А называется независимым от события В, если вероятность появления события А не зависит от того, произошло событие В или нет.

Теорема. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий

Р(АВ)=Р(А)·Р(В).

Заметим, что теорему о вероятности суммы совместных событий можно записать теперь в виде:

.

Примеры. 1. В первом ящике 2 белых и 7 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.

Обозначим события: А – вынули белый шар из первого ящика, ;

- вынули черный шар из первого ящика, ;

В – белый шар из второго ящика, ;

- черный шар из второго ящика, .

Нам нужно, чтобы произошло одно из событий или . По теореме об умножении вероятностей , . Тогда искомая вероятность по теореме сложения будет

.

2. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) хотя бы одного попадания; г) одного попадания.

Пусть А – попадание первого стрелка, Р(А)=0,8;

В – попадание второго стрелка, Р(В)=0,9.

Тогда - промах первого, ;

- промах второго, .

Найдем нужные вероятности.

а) АВ – двойное попадание, Р(АВ)=Р(А)Р(В)=0,72.

б) - двойной промах, .

в) А+В – хотя бы одно попадание,

.

г) - одно попадание,

.

3. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится 1) только в одном справочнике; 2) только в двух справочниках; 3) во всех трех справочниках.

А – формула содержится в первом справочнике;

В – формула содержится во втором справочнике;

С – формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

1.

=0,6·0,3·0,2+0,4·0,7·0,2+0,4·0,3·0,8=0,188.

2. .

3.З(АВС)=0,6·0,7·0,8=0,336.

4. Из 10 деталей 7 – стандартные. Наудачу берут 6 деталей. Найти вероятность того, что среди них: а) не более одной нестандартной; б) не более двух нестандартных.

а) Обозначим события А – среди взятых 6 деталей нестандартных нет;

В – в 6 выбранных деталях одна нестандартная. Тогда А+В – среди 6 деталей не более одной нестандартной. Найдем Р(А+В). Заметим, что

,

.

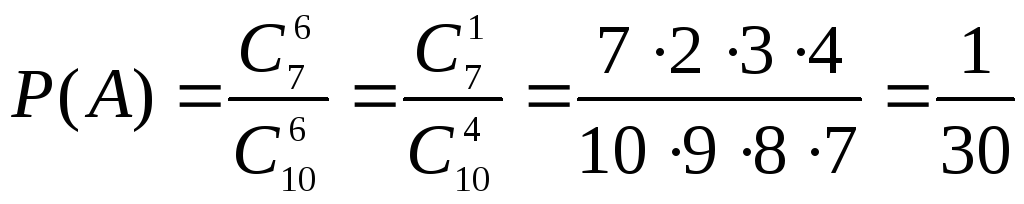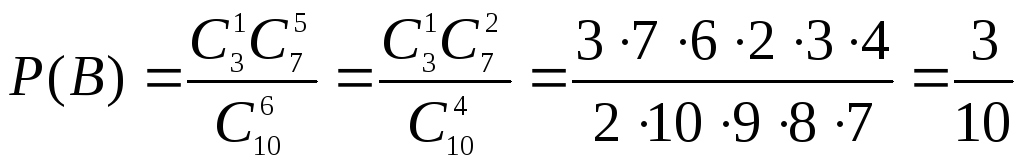Откуда

.

б) Пусть теперь событие А – в шести взятых деталях не более двух нестандартных. Тогда - в выбранных деталях более двух нестандартных, т.е. три.

.

.
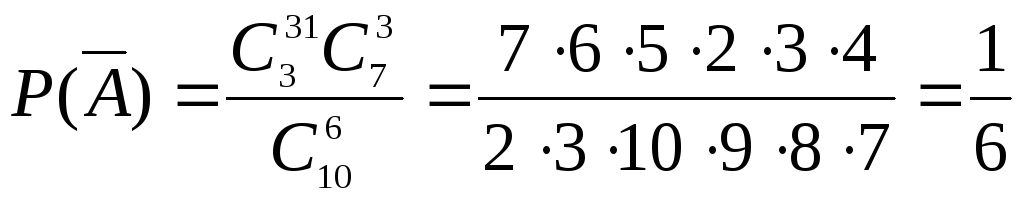