2.3. Нормальное уравнение прямой на плоскости и плоскости в пространстве. Приведение общего уравнения первого порядка к нормальному виду

2.3.1.Нормальное уравнение прямой на плоскости.

Рассмотрим общее уравнение прямой на плоскости.

, (1)

Определение. В случае нормальным уравнением прямой (1) называется уравнение

.

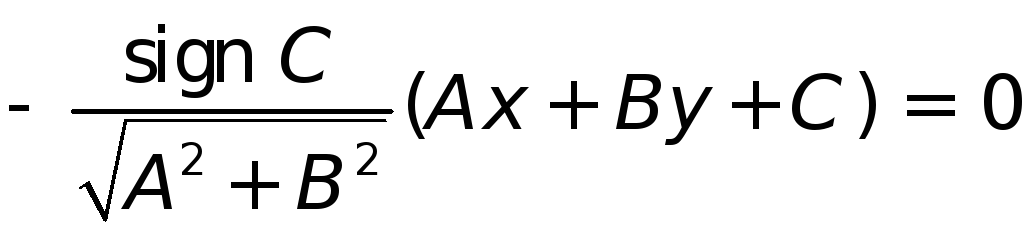Это уравнение можно записать в виде: (см. рис. 2.6)

Рис. 2.6. Нормальное (нормированное) уравнение прямой

Slide_2_6 «Нормальное уравнение прямой»

n = – единичный вектор нормали, ориентированный так, что будучи отложенным из начала координат, он будут «смотреть» в сторону прямой.

Slide_2_6_1 «Нормировка уравнения прямой»

Пример. Пронормировать уравнение прямой .

Модуль вектора нормали (3,4) равен 5. Делим уравнение прямой на 5 и берем знак противоположный знаку свободного коеффициента 25, получим нормальное уравнение прямой: .

С помощью нормального уравнения прямой определяют расстояние от точек до прямых, именно:

Расстояние от точки до прямойс нормальным уравнением равно

.

Slide_2_6_2 «Расстояние от точки до прямой»

Пример. Найти расстояние от точки до прямой(l).

.

2.3.2. Нормальное уравнение плоскости в пространстве

Рассмотрим общее уравнение плоскости в пространстве

, (1)

Определение. В случае нормальным уравнением плоскости (1) называется уравнение

.

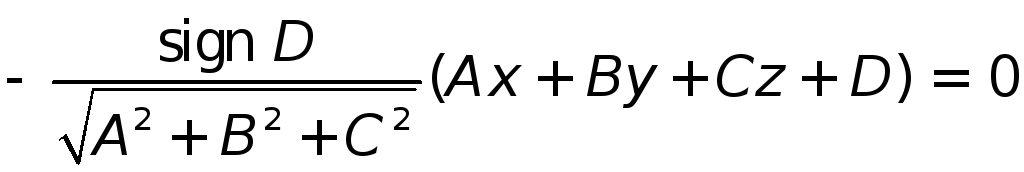Это уравнение можно записать в виде: (см. рис. 2.7)

Рис. 2.7. Нормальное уравнение плоскости (через направляющие косинусы нормали)

n = – единичный вектор нормали, ориентированный так, что будучи отложенным из начала координат, он будут «смотреть» в сторону плоскости.

Пример. Пронормировать уравнение прямой .

Модуль вектора нормали (1,2,1) равен . Делим уравнение прямой наи берем знак противоположный знаку свободного коеффициента -4, получим нормальное уравнение прямой:.

С помощью нормального уравнения плоскости определяют расстояние от точек до плоскостей, именно:

Расстояние от точки до плоскостис нормальным уравнением равно

.

Пример. Найти расстояние от точки до плоскости

.

2.4. Различные формы уравнения прямой на плоскости и в пространстве. Переход от одной формы к другой

2.4.1.Общее уравнение прямой на плоскости

Ранее уже рассматривалось уравнение прямой: , В векторной виде:.

2.4.2.Параметрическое уравнение прямой на плоскости

, В векторном виде: r = r₀ + l , .

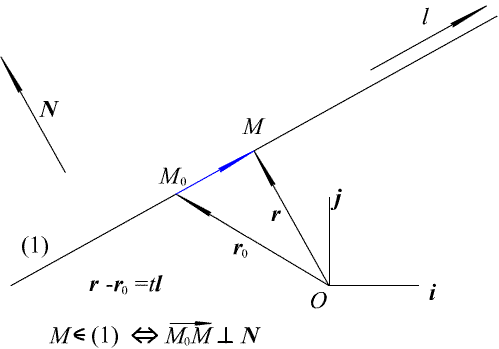
Рис. 2.8. Параметрическое уравнение прямой

Slide_2_8 «Параметрическое уравнение прямой на плоскости»

Вектор l называется направляющим вектором прямой (см. рис. 2.8).

2.4.3.Каноническое уравнение прямой на плоскости

Каноническое уравнение, в действительности, является несколько другой записью параметрического уравнения:

.

Для канонического уравнения прямой, так же как и для параметрического уравнения, нужна точка на прямой и направляющий вектор. Для краткости, в этом случае, будем говорить, что задана прямая .

Slide_10_1 «Каноническое уравнение прямой на плоскости»

2.4.4. Переход от одной формы уравнения прямой к другой на плоскости

Не тривиальным является только переход от общего к уравнения к параметрическому и обратно.

От общего к параметрическому.

Общее уравнение определяется нормалью N и точко на прямой. Если точка не задана, то ее можно найти, задав(в случае) или(в случае) и решив уравнениеотносительно оставшейся неизвестной. Например, для уравненияполагаеми находим,. После того, как точканайдена находим направляющий вектор прямойl . В качестве направляющего вектора берется любой вектор, ортогональный вектору нормали N . Для уравнения таким вектором может служить векторl=. В параметрическом виде уравнение будет выглядеть следующим образом:

, в каноническом: .

От параметрического к общему.

Для обратного перехода дроби формально преобразуются у виду:и далее получаем общее уравнение прямой:.

Пример. Привести к общему виду уравнение . После указанных преобразований получим:.

2.4.5.Уравнение прямой в пространстве, как пересечение двух плоскостей

Прямую в пространстве можно задать, указав две плоскости, линией пересечения которых, является данная прямая. При этом используют следующую запись:

Рис. 2.9. Прямая, как пересечение двух плоскостей

Для того, чтобы указанные плоскости определяли прямую, они должны быть не параллельны, то есть вектора не должны быть коллениарны (см. рис. 2.9).

2.4.6.Параметрическое уравнение прямой в пространстве

, в векторном виде: r = r₀ + l ,,(см. рис. 2.10).

Рис. 2.10. Парметрическое уравнение прямой

2.4.7.Каноническое уравнение прямой в пространстве

Каноническое уравнение, в действительности, является несколько другой записью параметрического уравнения:

.

Для канонического уравнения прямой, так же как и для параметрического уравнения, нужна точка на прямой и направляющий вектор. Для краткости, в этом случае, будем говорить, что задана прямая .

Slide_10_2 «Каноническое уравнение прямой в пространстве»

2.4.8. Переход от одной формы уравнения прямой к другой в пространстве

От общего к параметрическому

Задав какое нибудь значение одной из переменных , и решая систему

относительно оставшихся переменных можно будет найти какую нибудь точку на прямой. Направляющий вектор можно найти, как векторное произведение нормалей плоскостей, определяющих данную прямую:l = [ N₁ , N₂ ] .

Рис. 2.11. Переход от одного уравнения к другому

От параметрического к общему

Из дробей формально выписываем два равенства:, которые и дадут две плоскости, определяющие данную прямую (см. рис. 2.11).

2.4.9. Угол между двумя прямыми на плоскости и в простанстве, между двумя плолоскостями в пространстве, между прямой и плоскостью

Угол между двумя прямыми на плоскости равен углу между их нормалями. Угол между двумя прямыми в пространстве равен углу между их направляющими векторами. Угол между двумя плоскостями определяется, как угол между их нормалями. Угол между прямой и плоскостью в пространстве определяется, как угол между направляющим вектором прямой и нормалью к плоскости.