Представление графов

1. Задание графа с помощью матрицы смежности.

Пусть в графе число вершин равно :

Для задания графа будем использовать квадратную матрицу размера . Каждая строка и каждый столбец матрицы соответствуют определенной вершине графа. На пересечении строки и столбца ставим 1 тогда и только тогда, когда неупорядоченная пара является ребром графа. В противном случае ставим 0. Таким образом, число единиц в матрице определяется числом ребер графа. Матрица смежности неориентированного графа является симметрической (т.е. она совпадает со своей транспонированной матрицей).

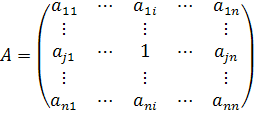
Действительно, если пара – ребро графа, тогда пара также является ребром графа (так как рассматривается неориентированный граф).

2. Задание графа с помощью матрицы инцидентности.

Пусть задан граф с вершинами и ребрами:

,

Матрица инцидентности для данного графа есть прямоугольная матрица размера размера , строки матрицы соответствуют вершинам, столбцы – ребрам.

На пресечении строки и столбца ставим 1 тогда и только тогда, когда вершина является одним из концов ребра , в противном случае – 0. Таким образом, каждый столбец матрицы инцидентности содержит либо две единицы, либо одну. Если столбец содержит одну единицу, то ребро, соответствующее данному столбцу, является петлей.

3. Задание графа с помощью списка смежности.

Для каждой вершины выписывается множество вершин, которые смежны с рассматриваемой. Вершина смежна с вершиной , если – ребро графа. Данный способ является наиболее экономным способом представления графов.

Определение. Полным графом называется граф, в котором все вершины соединены между собой неориентированными ребрами. То есть, множество ребер состоит из всевозможных неупорядоченных пар вершин графа. Число вершин графа (мощность множества вершин графа) будем обозначать . Число ребер в полном неориентированном графе на множестве вершин V задается формулой . Если , тогда:

То есть, по порядку, число вершин в полном графе квадратично относительно мощности множества вершин графа. Размер матрицы смежности неориентированного графа – . Общая память квадратична по , что является неэкономичным, когда граф разряжен, то есть число ребер мало.

Пример. Рассмотрим пустой граф на множестве вершин и пустом множестве ребер :

,

тогда матрица смежности потребует памяти, а список смежности будет содержать только перечисление вершин графа, поэтому память будет линейна относительно .

Аналогичным образом можно представлять ориентированные графы. Отличие будет в представлении матрицы инцидентности и списка смежности. В матрице инцидентности будем ставить 1 на пересечении строки и столбца , если вершина является началом некоторого ребра, а врешина – концом данного ребра и -1 будем ставить, если вершина является концом некоторого ребра, а вершина – его началом. Если нет ребра, соединяющего вершины и , то ставим 0.

В списке смежности для вершины выписываем вершины концов ребер, исходящих из вершины .

Определение. Два графа называются изоморфными, если между вершинами графов можно установить взаимооднозначное соответствие , сохраняющее соответствие смежности между вершинами.

Иначе говоря, графы изоморфны, если они одинаковы с точностью до переименования вершин.

Пример. Представленная пара графов изоморфна:

Изоморфизм определяется следующим соотношением между вершинами:

Следующие два графа не изоморфны:

Очевидно, что изоморфные графы должны иметь одно и то же число вершин и одно и то же число ребер. В представленных графах число ребер различно.

Определение изоморфности ориентированных графов аналогично.

Определение. Маршрутом в графе называется последовательность вершин , где пара соседних вершин является ребром графа.

-1

В этом случае будем говорить, что маршрут M соединяет вершины .

Пример.

Определение. Путем, соединяющим пару вершин будем называть маршрут, соединяющий данную пару вершин и не содержащий повторяющихся ребер.

Определение. Простым путем, соединяющим пару вершин будем называть путь, соединяющий данную пару и не содержащий повторяющихся вершин.

Определение. Пару вершин в графе будем называть связной, если либо вершины совпадают, либо существует маршрут, соединяющий две эти вершины.

Пример. Любая пара вершин в следующем графе связана:

В следующем графе связанными являются не все вершины:

Вершины 1 и 2 связаны, а, например, вершины 2 и 3 не связаны.

Утверждение. Если в графе существует маршрут, соединяющий пару вершин, то существует простой путь, который соединяет данную пару вершин.

Рассмотрим маршрут, соединяющий вершины . Предположим, что вершина повторяется на маршруте. Тогда вырежем участок маршрута между повторяющимися вершинами и соединим полученные части. Данную операцию будем повторять до тех пор, пока в маршруте не будет повторяющихся вершин.

Таким образом, получен простой путь, соединяющий пару вершин . Поэтому для связности вершин достаточно наличие простого пути, который их соединяет.

Определение. Циклом называется путь, в котором начальная и конечная врешины совпадают.

Пример.

Определение. Простым циклом называется путь, в котором вершины не повторяются, за исключением первой и последней. Другими словами, простой цикл - это цикл без самопересечения.

Пример. Простой цикл:.