20. Закон инерции вещественных квадратичных форм.

Закон инерции квадратичных форм. Пусть Q – квадратичная форма на вещественном линейном пространстве V , а e и f – различные базисы пространства V , в которых матрица формы Q диагональна. Тогда количество положительных (отрицательных) диагональных элементов в матрицах Qe и Qf одинаково.

21. Положительно определенные квадратичные функции. Критерий Сильвестра.

22. Евклидовы пространства, условие изоморфизма.( не точно!)

Вещественное линейное пространство  называется евклидовым, если каждой паре элементов  этого пространства поставлено в соответствие действительное число , называемое скалярным произведением, причем это соответствие удовлетворяет следующим условиям:

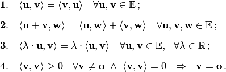
Вещественное линейное пространство со скалярным произведением называется евклидовым пространством. Нормой элемента a ∈ V называется число p ν(a, a).

Изоморфизмом линейных пространств называется биективный линейный оператор. Два линейных пространства U и V называются изо- морфными, если существует изоморфизм из U в V .

23. Неравенство Коши-Буняковского. Модуль вектора, расстояние и косинус угла между векторами.

Неравенство Коши–Буняковского.

Геометрический смысл:

|

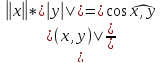Модулем (длиной) вектора  называется длина(норма) соответствующего отрезка  и обозначается как .

В евклидовом n-мерном пространстве длина вектора рассчитывается как корень из скалярного произведения этого вектора на себя, в том случае если это произведение задано как (x,y)=,где   координаты вектров x,y в каком-то базисе- то оно: .

Для любых двух ненулевых векторов x и y евклидова пространства E со скалярным призведением (x, y)  определен угол между векторами xи y:

Для любых двух ненулевых векторов x и y евклидова пространства E со скалярным призведением (x, y)  определено расстояние между векторами x и y:

24. Процесс ортогонализации Грама-Шмидта

Пусть – базис евклидова пространства V . Тогда элементы

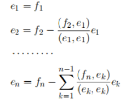
являются ортогональным базисом V . Более того, если – система образующих V , то ненулевые элементы набора образуют базис пространства V .

25. Ортогональное дополнение к подпространству евклидова

пространства.

Ортогональным дополнением подпространства U ≤ V называется множество всех векторов, ортогональных каждому вектору из U. Оно обозначается через 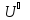. Ортогональное дополнение является подпространством. Кроме того, V = U ⊕ 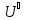. т. е. любой вектор v ∈ V однозначно представляется в виде суммы 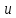= 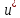+ w, где

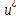∈ U, а w ∈ 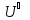. Элемент v ∗ называется ортогональной проекцией элемента 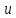на подпространство U

26. Ортогональные операторы и ортогональные матрицы. (не весь!)

Квадратная матрица называется ортогональной матрицей, если её столбцы образуют ортонормированную систему векторов пространства арифметических векторов соответствующей размерности.

Строки ортогональной матрицы также образуют ортонормированную систему векторов.

Матрица H ортогональна тогда и только тогда, когда

H^T·H = H·H^T = E, E— единичная матрица.