Высшая математика
.pdf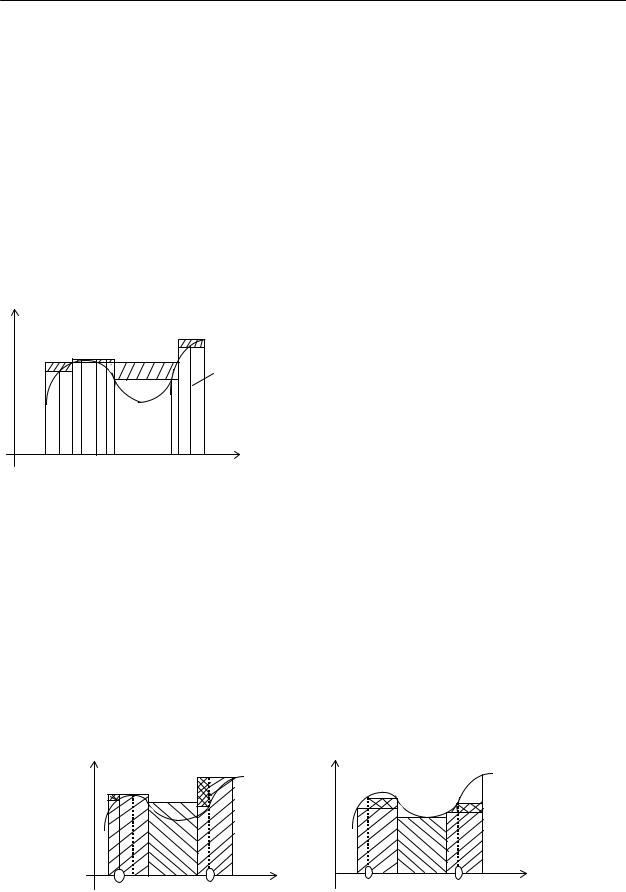
|
|
7. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ |
|
|||||||
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
S- S′=сумме площадей В |
С |
|
|
|
|
||
|
|
|
|
прямоугольников |
|
|
|
|
|
|
|
|
|
|
|
|
M -m |
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
A |
D |
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
x0 ξ1 x1 |
x2 ξ2 x3 |
∆ x4=b |
x |
|
|
|
|
|
|
|
|
Рис.7 |
|
|
|
|
|
|
На рис.7 точки x0 = a < x1 < x2 < x3 < x4 = b соответствуют разбиению Т сегмента |
|||||||||
[a,b], |
а |
две |
добавленные |
точки |
ξ1 и ξ2 |
образуют |
вместе |
с |
точками |
xi: |
x0=a<ξ1<x1<x2<ξ2<x3<x4=b разбиение Т′ |
этого сегмента. |
|
|
|
|
|||||
|
Одинарной штриховкой показана верхняя сумма S разбиения Т, а двойной штри- |
|||||||||
ховкой два прямоугольника, сумма площадей которых дает уменьшение S до величины |
||||||||||
S′ . Если через М и m обозначить точные верхнюю и нижнюю грани функции f(x) на [a,b], |
||||||||||
а через ∆ максимальную длину частичного сегмента [xi-1,xi] разбиения Т, то площадь пря- |
||||||||||
моугольника ABCD, равная (M-m)∆x будет больше площади каждого из двух прямо- |
||||||||||
угольников, заштрихованных двойной штриховкой, отсюда очевидна оценка: S-S′ ≤(M- |
||||||||||
m)∆ 2 (здесь 2 – число добавленных точек). Для нижних сумм может быть дана аналогич- |
||||||||||
ная интерпретация. |
|
|
|
|
|
|
|
|||
|
В заключение данной темы приведем без доказательства формулировку теоремы, из- |
|||||||||
вестной под названием леммы Дарбу, имеющей фундаментальное значение для построения |
||||||||||
теории в теме “Определенный интеграл”. |
|
|
|
|
|
|
||||
|
Лемма Дарбу. Верхний и нижний интегралы Дарбу I |
и I от функции f(x) по сег- |
||||||||
менту [a,b] являются соответственно пределами верхних и нижних сумм при ∆→0, т.е. |
||||||||||
lim S = I |
и lim |
s = I . |
|
|
|
|
|
|
|
|
∆→0 |
|
∆→0 |
|
|
|
|
|
|
|
|
|
Замечание 1. Число I , например, называется пределом верхних сумм S при ∆→0, |
|||||||||
если ( ε > 0)( δ > 0): [( T )∆ < δ S − I < ε]. |
|
|
|
|
|
|||||
|
Замечание 2. В случае, когда I = I = I лемма Дарбу позволяет переходить к преде- |
|||||||||
лам в неравенствах вида s ≤ I{xi , ξi } ≤ S |
при стремлении к нулю диаметра ∆ разбиения Т |
|||||||||
сегмента [a,b]. При этом s→I и S→I, откуда I{xi , ξi } → I . |
|
|
|
|
||||||
7.3. Необходимое и достаточное условие интегрируемости функции на сегменте
Вышеперечисленные свойства верхних и нижних сумм позволяют доказать теорему об интегрируемости функции на сегменте.
Теорема. Для того, чтобы ограниченная на сегменте [a,b] функция f(x) была интегрируемой на этом сегменте, необходимо и достаточно, чтобы ε > 0 нашлось такое разбиение Т сегмента [a,b], для которого S – s ≤ ε.
173
7. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
|
f(x′′) − f(x′) |
|
= |
|
f ′(ξ) |
|
|
|
x′′ − x′ |
|
= |
1 |
|
|
x′′ − x′ |
|
< |
|
x′′ − x′ |
|
, ибо x′ <ξ< x′′ и ξ>1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ξ |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, по данному ε>0, если выбрать 0<δ≤ ε, то из x′′ − x′ < δ f(x′′) − f(x′) < ε
Пример 2. Функция f(x)=1
x на интервале (0,1) непрерывна, но не является на нем равномерно непрерывной, т.е. для некоторого ε>0 нельзя выбрать δ>0 такое, что неравен-
ство |
|
f(x′′) − f(x′) |
|
< ε |
будет выполнено для всех x′′ и x′ при условии, что |
|
x′′ − x′ |
|
< δ . |
|
|
|
|
||||||
|
|
Покажем это. |
Пусть δ>0, x′ = δ, x′′= δ 2 , тогда x′′ − x′ < δ 2 , а величина |
||||||
f(x′′) − f(x′) = 2 δ −1 δ =1 δ может быть сделана сколь угодно большой.
y
y2
εδ2→0 при y2→∞
y1 |
|
y = |
1 |
ε |
|
|
x |
|
|
|
|
δ2 |
δ1 |
|
x |
Для непрерывной на сегменте функции справедлива следующая теорема.
Теорема (Кантора). Непрерывная на сегменте [a,b] функция f(x) равномерно непрерывна на этом сегменте.
Теперь, с очевидностью, вытекает следствие: пусть функция f(x) непрерывна на [a,b], тогда ( ε > 0)( δ > 0) такое, что на каждом, принадлежащем сегменту [a,b] частич-
ном сегменте [c,d], длина d-c которого меньше δ, колебание ω функции f(x) меньше ε. Сформулируем и докажем следующую основную теорему.
Теорема. Непрерывная на сегменте [a,b] функция f(x) интегрируема на этом сегменте. Пусть дано ( ε > 0) . Так как f(x) равномерно непрерывна на сегменте [a,b] (теорема
Кантора), то для положительного числа ε
(b −a) можно указать такое δ>0, что при разбиении Т сегмента [a,b] на частичные сегменты [xi-1,xi], длина максимального из которых ∆<δ, колебание ωi функции f(x) на каждом из них меньше ε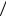
(b −a) (следствие из теоремы
n |
ε |
n |
Кантора). Тогда для таких разбиений Т S − s = ∑ωi ∆xi < |
|
∑ ∆xi = ε и выполняется |
|
||
i=1 |
b −a i=1 |
|
достаточное условие интегрируемости функции f(x).
Замечание. Если f(x) имеет на [a,b] конечное число точек разрыва 1-го рода, то функция f(x) также интегрируема на этом сегменте. При этом, если, например, f(x) раз-
b |
c |
b |
рывна в одной точке x=c, то ∫ f(x)dx = ∫ f(x)dx + ∫ f(x)dx , и значение этих интегралов не
a |
a |
c |
зависит от значения функции в точке с.
175
7.ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
7.5.Основные свойства определенного интеграла
|
a |
|
|
1) |
∫ f(x)dx = 0 |
|
(по определению). |
|
a |
|
|
|
b |
a |
|
2) |
∫ f(x)dx = −∫ f(x)dx |
(по определению, при a<b). |
|
ab
bb
3) |
∫ cf(x)dx = c∫ f(x)dx |
|
(с = const). |
|
|
a |
a |
|
|
|
b |
b |
b |
|
4) |
∫ |
[f(x) ± g(x)]dx = ∫ f(x)dx ± ∫ g(x)dx |
|
|
|
a |
a |
a |
|
|
b |
c |
b |
|
5) |
∫ f(x)dx = ∫ f(x)dx + ∫ f(x)dx |
для произвольных с, при условии интегрируемо- |
||
|
a |
a |
c |
|
сти функции f(x). |
|
|
||
|
b |
|
|
|
6) ∫ f(x)dx ≥ 0, если f(x) ≥0 x [a,b].
a
7) Если функция f(x) c[a,b], то свойство 6) можно уточнить при f(x) ≡ 0.
b |
|
b |
|
если f(x) ≥g(x) x [a,b]. |
|||||||
8) ∫ f(x)dx ≥ ∫ g(x)dx |
|
||||||||||
a |
|
a |
|
|
|
||||||
|
|
b |
|
b |
|
|
|
||||
|
|
|
|
|
|||||||
9) |
|
∫ f(x)dx |
≤ ∫ |
|
f(x) |
|
dx . |
|
|
||
|
|
|
|
||||||||
|
|
a |
|
a |
|
|
|
|
|
|
|
|
|
b |
|
|
|
b |
|
b |
|
||
10) m∫ g(x)dx ≤ ∫ f(x)g(x)dx ≤ M ∫ g(x)dx, |
|
||||||||||
|
|
a |
|
|
|
a |
|
a |
|
||
если |
g(x) ≥0 |
x [a,b], |
M = sup f(x) , m = inf f(x) . |
||||||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
[a,b] |
[a,b] |
7.6. Первая и вторая формулы среднего значения
Докажем формулу, которая называется первой формулой среднего значения. Пусть функции f(x) и g(x) интегрируемы на сегменте [a,b], и функция g(x) не меня-
ет знака на этом сегменте. Если M = sup f(x) , m = inf f(x) , то существует число µ, удов-
|
[a,b] |
[a,b] |
летворяющее неравенствам m ≤ µ ≤ M, такое, что справедлива формула |
||
b |
b |
|
∫ f(x)g(x)dx = µ∫ g(x)dx . |
(1) |
|
a |
a |
|
Если, в частности, f(x) непрерывна на сегменте [a,b], то ξ [a,b], что будет выполняться равенство
b |
b |
|
∫ f(x)g(x)dx = f(ξ)∫ g(x)dx . |
(2) |
|
a |
a |
|
|
|
176 |
7. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
Замечание. Формула (1) (и (2)) называется первой формулой среднего значения.
Доказательство. Будем предполагать, что g(x)≥0 (в случае g(x) ≤ 0 рассуждения аналогичные).
b
а) Если ∫ g(x)dx = 0 , то в силу свойства 10 определенного интеграла (см. тему 5)
a
b
∫ f(x)g(x)dx = 0 ,
a
и тогда в качестве µ можно взять любое число.
b
в) Пусть ∫ g(x)dx > 0 , тогда из 10)
a |
|
b |
b |
m ≤ ∫ f(x)g(x)dx |
∫ g(x)dx ≤ M . |
a |
a |
b |
b |
Обозначая через µ = ∫ f(x)g(x)dx |
∫ g(x)dx , будем иметь формулу (1). |
a |
a |
Формула (1) доказана. |
|
Для доказательства формулы (2) нужно показать, что в случае непрерывной функции f(x) найдется такая точка ξ [a,b], что f(ξ)=µ в формуле (1). Однако это вытекает из того, что непрерывная на сегменте [a,b] функция достигает на этом сегменте как своих точных граней M и m, так и любого промежуточного между ними значения µ (m ≤ µ ≤ M).
Следствие. В частном случае, когда g(x)≡1, формула (1) принимает вид:
b
∫ f(x)dx = µ (b −a) ,
a
а (в предположении непрерывности функции f(x) на сегменте [a,b]) формула (2) превращается в
b
∫ f(x)dx = f(ξ) (b −a)
a
Замечание. Если f(x) не является непрерывной, то формула (1) вообще говоря, невер-
на.
Пример.
|
f(x) |
|
|
|
|
|
g(x) |
|
|
|
||||
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
1 |
x |
2 |
1 |
x |
|||||||||
177
7. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
1 |
|
|
|
≤ x ≤ |
1 |
|
|
≤ x ≤ |
1 |
|
||||
|
|
, |
0 |
|
1, 0 |
|
|
|
||||||
|
|
|
|
|
||||||||||
f(x) = 2 |
|
|
|
|
2 |
g(x) = |
|
|
|
2 |
|
|||
|
|
1 |
|
< x ≤1 |
|
1 |
|
1 |
< x |
≤1 |
||||
1, |
|
|
|
|
, |
|
||||||||
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
|
||||
b |
1 |
1 |
1 2 |
1 |
1 |
|
|
1 |
|
3 |
|
|
2 |
|
||
|
|
|
|
|
|
|
= µ |
|
|
|
||||||
∫ f(x)g(x)dx = ∫ |
|
dx = µ |
∫1 dx + |
∫ |
|
dx |
|
|
|
; |
µ = |
|
. |
|||
2 |
2 |
2 |
4 |
3 |
||||||||||||
a |
0 |
|
0 |
1 2 |
|
|
|
|
|
|
||||||
и для ξ [0,1] |
f(ξ)≠µ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Сформулируем без доказательства теорему, позволяющую получить формулу, известную под названием второй формулы среднего значения, или формулы Бонне. Эта формула будет неоднократно использоваться в разных разделах математического анализа, в частности, в разделе “Несобственные интегралы”.
Теорема. Если на сегменте [a,b] функция g(х) монотонна, а f(x) интегрируема, то
на этом сегменте существует такая точка ξ, что
b ξ b
∫ f(x)g(x)dx = g(a)∫ f(x)dx + g(b)∫ f(x)dx
a a ξ
– вторая формула среднего значения или формула Бонне.
7.7. Интеграл с переменным верхним пределом.
Одним из важных понятий для непрерывных и интегрируемых на сегменте [a,b] функций является понятие интеграла с переменным верхним пределом, используя которое, можно получить основную формулу интегрального исчисления – формулу НьютонаЛейбница.
Определение. Пусть функция f(x) интегрируема на любом сегменте [α,β] (a,b) и пусть c – некоторая фиксированная точка, принадлежащая интервалу (a,b), тогда, каково бы ни было число х (a,b), функция f(x) интегрируема на [c,x], и на интервале (a,b) опре-
x
делена функция F(x) = ∫ f(t)dt , которая называется интегралом с переменным верхним
c
пределом.
Теорема. Любая непрерывная на интервале (a,b) функция f(x) имеет на этом интер-
x
вале первообразную. Одной из первообразных является функция F(x) = ∫ f(t)dt , где с –
любая фиксированная точка интервала (a,b). |
|
|
|
c |
|||
|
F(x + ∆x) − F(x) |
|
|
||||
Достаточно доказать, что для x (a, b) lim |
= f(x) (∆х берем таким, |
||||||
∆x |
|||||||
|
|
∆x→0 |
|
|
|||
чтобы (х+∆х) (a,b)). Рассмотрим разность |
|
|
|
|
|||
x+∆x |
x |
x |
x+∆x |
x |
|
x+∆x |
|
F (x + ∆x) − F (x) = ∫ f (t)dt − ∫ f (t)dt = ∫ f (t)dt + |
∫ f (t)dt − ∫ f (t)dt = |
∫ f (t)dt = f (ξ)∆x, |
|||||
c |
c |
c |
x |
c |
|
x |
|
|
|
178 |
|
|
|
|
|
7. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
где ξ – некоторое число, заключенное между х и х+∆х (Здесь было использовано свойство 6 определенного интеграла и первая формула среднего значения для непрерывной на сег-
менте функции). |
|
|
|
|
|
при ∆х→0 f(ξ)→f(x), и поэтому |
|
|
Так как f(x) |
непрерывна в |
точке х, |
то |
|||
lim |
F(x + ∆x) − F(x) |
= f(x) . |
|
|
|
|
|
∆x |
|
|
|
|
|
||
∆x→0 |
|
|
|
|
|
|
|
|
Замечание 1. Аналогично доказывается теорема для непрерывной на сегменте [a,b] |
||||||
|
|
|
|
|
|
|
x |
функции f(x). В этом случае в качестве с можно взять точку а и F(x) = ∫ f(t)dt . |
|||||||
|
|
|
|
|
|
|
a |
|
|
|
|
d x |
|
|
|
|
Замечание 2. Мы показали, что |
|
|
∫ f(t)dt |
= f(x) . |
||
|
|
|
|||||
|
|
|
|
dx c |
|
|
|
Замечание 3. Если f(x) интегрируема на любом сегменте, содержащемся в интервале (a,b), то интеграл с переменным верхним пределом представляет собой непрерывную функцию на интервале (a,b) от верхнего предела. В самом деле
|
|
|
x+∆x |
x |
∆F = F(x + ∆x) − F(x) = ∫ f(t)dt − ∫ f(t)dt = µ ∆x, |
||||
|
|
|
c |
c |
|
M = sup f(x) |
|
||
где m≤ µ ≤ M |
|
[a,b] |
|
|
|
|
|
|
|
|
m = inf f(x) |
|
||
|
|
[a,b] |
|
|
Отсюда |
lim |
∆F = lim (µ ∆x) = 0 , и в силу разностной формы условия непрерыв- |
||
|
∆x→0 |
|
∆x→0 |
|
ности F(x) есть непрерывная на интервале (a,b) функция.
7.8. Основная формула интегрального исчисления или формула Ньютона-Лейбница
В разделе “Неопределенный интеграл” было показано, что любые две первообразные функции f(x) на сегменте [a,b] отличаются лишь на константу. В предыдущей теме данного пособия была доказана теорема, что интеграл с переменным верхним пределом
x
F(x)= ∫ f(t)dt является одной из первообразных функции f(x) на сегменте [a,b] (с,х [a,b]),
c
поэтому любая первообразная ϕ(х) непрерывной на сегменте [a,b] функции f(x) может
x
быть представлена в виде ϕ(x) = ∫ f (t)dt +c , где с – произвольная постоянная. Используя
a
|
|
a |
свойство 1 определенного интеграла, имеем |
ϕ(a) = ∫ f (t)dt +c = c . Очевидно также, что |
|
|
|
a |
b |
b |
b |
при х=b ϕ(b) = ∫ f (t)dt +c = ∫ f (x)dx +c , откуда ∫ f (x)dx = ϕ(b) −c . |
||
a |
a |
a |
179
7. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ
Подставляя вместо с Ф(а) в последнее равенство, получим формулу
b
∫ f (x)dx = ϕ(b) −ϕ(a) .
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
Для удобства |
записи |
|
разность |
ϕ |
|
(b)- |
|
ϕ(а) |
|
записывают в форме ϕ(x) |
|
ab , и |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ f (x)dx = ϕ(x) |
|
ab |
|
– основная формула интегрального исчисления или формула Ньютона- |
|||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лейбница. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Примеры: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
3 |
|
dx |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
π = |
|
π |
|
|
|
|
|
|
|
|
|
|
||||
1. |
∫ |
|
|
|
= arctgx |
|
= arctg |
|
3 |
−arctg1 = |
− |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
1+ x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
4 |
|
12 |
|
|
|
|
|
|
|
|
|
|
||||||
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
1 |
(−1 |
−1) =1 |
||||||||
2. |
|
|
|
|
|
|
|
|
|
cos2x |
2 = − |
|
|
|
|
|
|
|
|
|
|
= − |
|||||||||||||||||||||||
∫ sin 2xdx = − |
2 |
|
cos2 |
2 |
−cos2 0 |
2 |
|
||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
dx |
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3. |
∫ |
|
|
|
= arcsin |
= arcsin |
−arcsin 0 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
16 − x2 |
4 0 |
2 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
|
cos x |
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
(1 |
−4) |
|
3 |
|
|
|
|||||||
4. ∫ |
|
|
|
|
|
dx = − |
|
|
|
|
|
|
= − |
|
|
|
|
|
|
− |
|
|
|
|
|
|
= − |
|
= |
|
|
|
|
||||||||||||
sin |
3 |
x |
sin x |
|
2 |
|
|
2 π |
|
|
|
|
|
2 |
2 |
|
|
|
|||||||||||||||||||||||||||
|
π |
|
|
|
|
|
|
π |
|
|
|
|
|
|
sin |
2 |
π |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
sin |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7.9. Формулы замены переменной и интегрирования по частям в определенном интеграле
Теорема. Пусть функция f(x) непрерывна на сегменте [a,b]. Сегмент [a,b] является множеством значений некоторой функции x=g(t), определенной на сегменте α ≤ t ≤ β, при-
чем g(α)=a, g(β)=b.
|
Пусть |
также g′(t) непрерывна |
t [α,β]. Тогда справедлива |
формула: |
|
b |
β |
|
|
|
|
∫ f(x)dx = ∫ f[g(t)]g′(t)dt |
– формула замены переменной под знаком определенного инте- |
||||
a |
α |
|
|
|
|
грала. |
|
|
|
|
|
|
Доказательство. |
Пусть ϕ (x) – |
некоторая первообразная функции |
f(x), т.е. |
|
|
|
b |
|
|
|
ϕ′(x) = f (x) |
и ∫ f (x)dx = ϕ(b) −ϕ(a) . Так как функции ϕ (х) и x=g(t) дифференцируемы на |
||||
a
соответствующих сегментах, то сложная функция ϕ [g(t)] дифференцируема на сегменте [α,β]. Применяя правило дифференцирования сложной функции, получим
d |
ϕ[g(t)] =ϕ′(g(t)) g′(t), |
(1) |
|
dt |
|||
|
|
||
|
|
180 |