Вариационная постановка начально-краевой задачи

Вариационная постановка начально-краевой задачи для параболического уравнения основана на функционале

,

где функции Q=Q(x,y,t) иg_Г=g_Г(x,y,t) считаются известными и поэтому не варьируются. Экстремум этого функционала достигается на решении рассматриваемой начально-краевой задачи. Это можно показать следующим способом

Вариация функционала будет иметь вид

.

Применение к первым двум слагаемым второго интеграла приёма интегрирования «по частям» и принятие

позволяют записать вариацию функционала в виде

.

Использование этой записи вариации функционала в необходимом условии существования его экстремума

,

позволяет получить параболическое уравнение

и возможные варианты граничных условий

.

Первое граничное условие приводится к условию 1-го типа

,

а второе граничное условие совпадает с условием 2-го типа.

Алгоритм метода конечных элементов

Алгоритм решения начально-краевой задачи для параболического уравнения методом конечных элементов во многом совпадает с применением этого метода к решению краевой задачи для эллиптического уравнения.

Сначала область поиска решения в пространстве {x, y} разбивается на треугольные элементы, для каждого из которых вводится своя локальная система координат ξ0η. Внутри каждого n-го элемента искомое решение u(ξ, η, t) представляется билинейной функцией

,

коэффициенты s₁, s₂ и s₃ которой, в отличие от решения эллиптического уравнения, являются функциями времени t. В матричной форме с заменой коэффициентов s₁, s₂ и s₃ значениями искомой функции в узлах конечного элемента такое представление решения имеет вид

,

где

, ,.

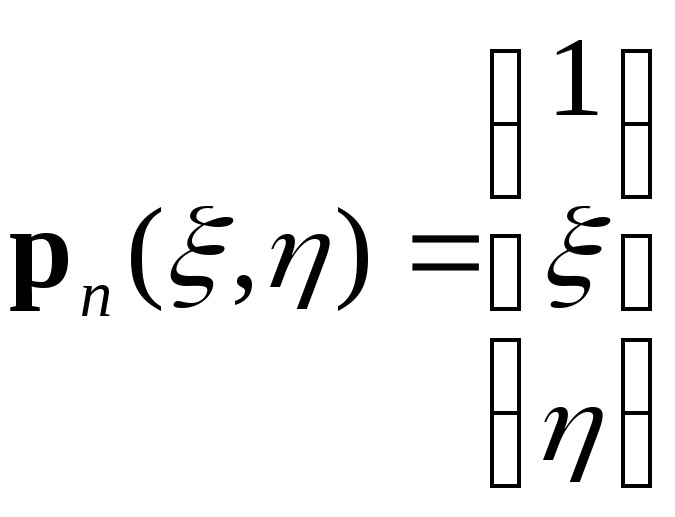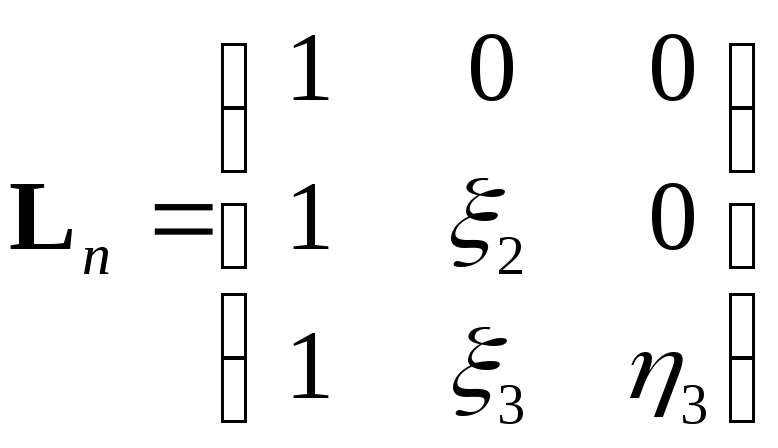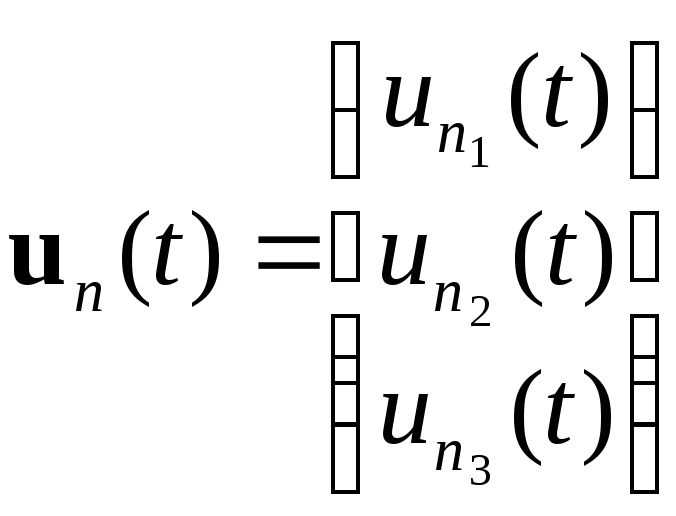Коэффициенты d, c, a, q, g, h и r параболического уравнения и его граничных условий в пределах каждого элемента описываются аналогичным образом

,

,

,

.

После этого для каждого конечного элемента записывается функционал, эквивалентный рассматриваемой начально-краевой задаче

.

Здесь, как и ранее, интеграл по контуру элемента представлен суммой интегралов по каждой его стороне.

Подстановка билинейного представления искомого решения в это выражение для функционала и выполнение операций интегрирования по площади и по контуру конечного элемента позволяет записать функционал в виде

,

где

,

,

,

,

,

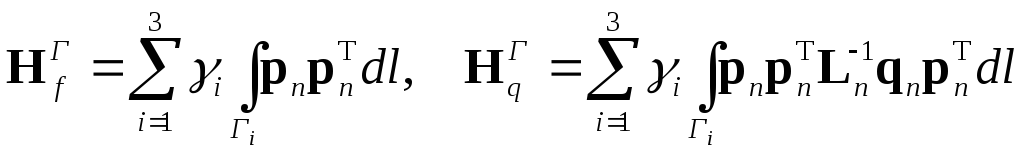Здесь D_n, K_n и B_n – квадратные симметричные матрицы (3×3 элем.), последние две из которых принято называть матрицами жёсткости элемента и его границы, а z_n и b_n – векторы внешнего воздействия (по 3 элем.) на конечный элемент.

Следующий этап метода конечных элементов предполагает «сборку» конечно-элементной схемы, которая имеет целью получение функционала задачи для всей области поиска решения. Для этого функционалы для каждого элемента суммируются

,

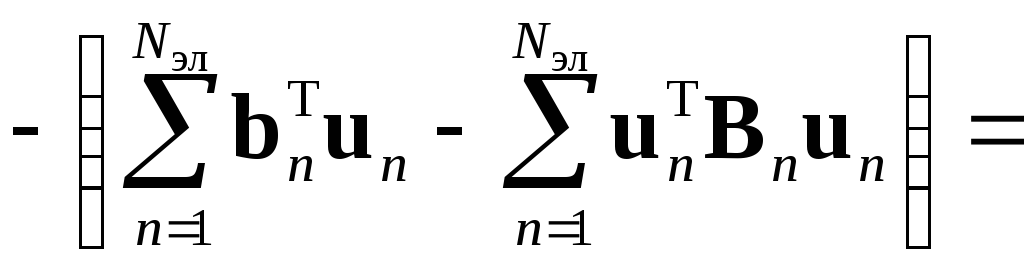
где D₀, K₀ и B₀ – объединённые матрицы, аналогичные ранее введённым матрицам D_n, K_n и B_n, z₀ и b₀ – объединённые векторы внешнего воздействия на элементы, а u₀ – объединённый вектор решения в узлах конечных элементов

,

.

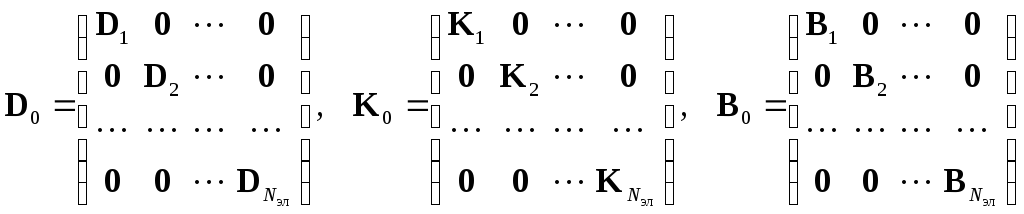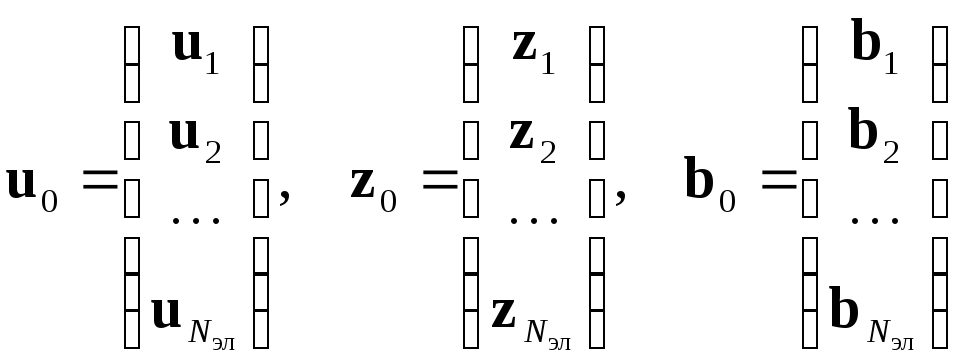После этого на основе способа объединения конечных элементов в область поиска решения S формируется матрица геометрии Г, которая связывает объединённый вектор решения u₀ с вектором u обобщённого решения в узлах самой области S

,

где

.

В итоге функционал начально-краевой задачи для всей области S поиска решения будет равен

,

где D = Г^ТD₀Г, K = Г^ТK₀Г и B = Г^ТB₀Г – матрицы для всей области S поиска решения и её границы Г, аналогичные ранее введённым матрицам D_n, K_n и B_n, а z = Г^Тz₀ и b = Г^Тb₀ – векторы внешнего воздействия на них.

Для получения конечно-элементных уравнений рассматриваемой начально-краевой задачи необходимо потребовать минимума её функционала в виде необходимого условия его экстремума

.

При этом надо помнить, что произведение и выражение в скобках по определению этого функционала не подлежат варьированию.

Подстановка в это вариационное уравнение ранее полученного выражения для функционала и выполнение в нём операции варьирования вектора обобщённого решения с учётом симметричности матриц D, K и B позволяет получить следующее уравнение

или

.

Сравнение множителей при вариациях одинаковых компонент обобщённого вектора решения даёт следующее матричное уравнение

,

где

.

Полученное уравнение представляет собой систему обыкновенных линейных дифференциальных уравнений относительно значений решений в узлах конечно-элементной сетки – u_i , которые образуют обобщённый векторu решения для всей области S. Для построения его решения u(t) это уравнение должно быть дополнено начальным условием, имеющем N_уз компонент, как и вектор решения

,

где вектор u_нач формируется из значений решения u₀(x, y) в начальный момент времени в узлах конечно-элементной сетки.

Методы решения такой задачи известны по разделу «Решение задачи Коши для нормальных систем обыкновенных дифференциальных и уравнений высших порядков» [3]. Однако прежде чем решать полученную задачу Коши, её надо преобразовать так, чтобы она учитывала граничные условия.

В методе конечных элементов граничные условия ставятся в узловых точках контура Г, ограничивающего область поиска решения S. При этом граничные условия 2-го типа в узловых точках выполняются автоматически в силу вариационной постановки задачи. Поэтому в контурных точках внешней границы области S надо учитывать только граничные условия 1-го типа, если они в них заданы.

Это делается так же, как при решении краевой задачи для эллиптического уравнения. Если в какой-либо точке границы с номером n задано граничное условие 1-го рода

,

которое должно быть согласовано с начальным условием

,

то коэффициенты матриц D и и векторасоответствующие узловому значению решенияu_n преобразуются следующим способом.

Диагональный элемент n-ой строки матрицы D заменяется единицей, а остальные элементы этой стоки и соответствующего столбца обнуляются. Элементы этой же строки и такого же столбца матрицы тоже обнуляются, аn-й элемент вектора заменяется производной по времени

.

Оценка погрешности решения

Основными составляющими погрешности конечно-элементного решения начально-краевой задачи для параболического уравнения являются погрешность аппроксимации решения для конечного элемента, погрешность представления области поиска решения конечными элементами и погрешность решения задачи Коши. Её оценка для такого разнопланового вычислительного процесса затруднительна. Поэтому на практике для вычисления погрешности используют оценку, базирующуюся на правиле Рунге и описанную для эллиптического уравнения

,

.

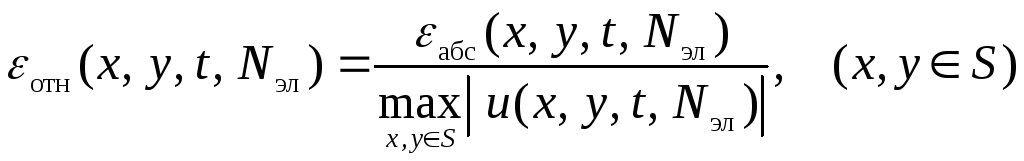Однако здесь надо помнить, что такой подход к оценке погрешности решения начально-краевой задачи для параболического уравнения применим только тогда, когда интервальная оценка погрешности численного решения задачи Коши на отрезке [0, t] пренебрежимо мала по сравнению с получаемой величиной погрешности.