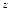(46.12)
220 Гл. 5. Интегральное исчисление функций многих переменных
Здесь и в дальнейшем i, j, k, как обычно, обозначают единичные векторы координатных осей (правой или левой) ортонормированной
системы координат x, y, z. Так как |
|
|
|
|
|
|
|
|
|
0 0 |
|
y0 |
z0 |
, |
|
|
x0 |
z0 |
, |
|
x0 |
y0 |
( |
|
|
u |
u |
− |
|
u |
u |
|
u |
u |
, |
ru ×rv = |
'yv0 |
zv0 |
xv0 |
zv0 |
xv0 |
yv0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то уравнение нормальной |
прямой |
имеет |
вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а в случае поверхности, заданной явным представлением z = f (x, y), (x, y) G, — вид
x − x0 |
= |
y − y0 |
= (z |
− |
z0), |
(46.10) |
fx0 |
|
fy0 |
− |
|
|
где fx0 = fx(x0, y0), fy0 = fy(x0, y0).
Иногда поверхность задается в неявном виде с помощью уравнения
в том смысле, что координаты (x, y, z) точек рассматриваемой поверхности удовлетворяют уравнению (46.11). Если функция F непрерывно дифференцируема в окрестности точки (x0, y0, z0), F (x0, y0, z0) = 0 и одна из частных производных функции F в точке (x0, y0, z0) не равна нулю, например, Fz(x0, y0, z0) = 0, то согласно теореме о неявных функциях в некоторой окрестности точки (x0, y0, z0) уравнение (46.11)
можно записать в виде
z = f (x, y),
т. е. локально множество точек (x, y, z), удовлетворяющих уравнению (46.11), является параметрически заданной поверхностью с явным представлением. Вспомнив, что для частных производных функции (46.12) имеют место формулы
|
|
|
∂F |
|
|
∂F |
|
∂f |
= − |
|
|
|
|
∂f∂y = − |
∂y |
, |
∂x |
, |
∂x |
|
∂F |
|
|
∂F |
|
|
|
|
∂z |
|
|
∂z |
из уравнения (46.8) получим, что уравнение касательной плоскости поверхности, заданной неявно уравнением (46.11), имеет вид
|
|
|
|
|
|
|
|
(x − x0)Fx0 + (y − y0)Fy0 + (z − z0)Fz0 = 0, |
(46.13) |
где Fx0 = Fx(x0, y0, z0), Fy0 = Fy(x0, y0, z0), |
Fz0 = Fz (x0, y0, z0), |
а урав- |
нение нормальной прямой — вид |
|
|
|
(x − x0) |
= |
(y − y0) |
= |
(z − z0) |
. |
|
Fx0 |
|
Fy0 |
Fz0 |
|
§ 46. Элементы теории поверхностей |
221 |
46.3. Первая квадратичная форма поверхности. Рассмотрим дифференциал dr векторного представления r(u, v), (u, v) G,
поверхности S:
dr = ru du + rv dv.
Найдем квадрат длины вектора dr:
(dr)2 = (ru du + rv dv)2 = r2u du2 + 2rurv du dv + r2v dv2.
Введем обозначения
g |
= r2 |
, g = r |
u |
r |
v |
, g = r2 . |
(46.14) |
11 |
u |
12 |
|
22 |
v |
|
Тогда |
|
|
|
|
|
|
|
(46.15) |
(dr)2 = g11 du2 + 2g12 du dv + g22 dv2. |
Квадратичная форма (46.15) называется первой квадратичной формой поверхности (есть еще вторая и третья квадратичные формы
поверхности, но мы не будем их изучать в нашем курсе). Мы увидим, что, зная коэффициенты g11, g12 и g22 первой квадратичной формы поверхности в каждой точке поверхности, можно решать ряд задач, например находить длины кривых на поверхности и вычислять площадь поверхности.
Л е м м а 1. Первая квадратичная форма поверхности является положительно полуопределенной формой, а во всякой неособой точке поверхности — положительно определенной.
Положительная полуопределенность квадратичной формы (46.15) очевидна, так как (dr)2 0. Докажем ее положительную определенность в неособой точке.
Если точка поверхности неособая, то в ней векторы ru и rv линейно независимы. Поэтому в этой точке равенство dr = 0 имеет место тогда и только тогда, когда du = dv = 0, ибо dr = ru du + rv dv. Следовательно, если в неособой точке поверхности du2 + dv2 > 0, то (dr)2 > 0. Это и означает положительную определенность первой квадратичной формы поверхности.
З а м е ч а н и е. Докажем полезную для дальнейшего формулу, выражающую дискриминант первой квадратичной формы поверхности
через длину векторного произведения векторов ru и rv: |
|
|
|
g12 |
|
|
|
g11 |
. |
(46.16) |
|
|ru ×rv|2 = g12 |
g22 |
|
|
|
|
|
Для любых двух векторов a и b имеем |
|
|
|a×b| = |a||b| sin ab, |
|
|
ab = |a||b| cos |
, |
|
Возводя эти равенства |
|
ab. |
|
тождество |
в квадрат и |
сложив, получим |
|
, |
|
|
Лагранжа |a×b|2 = |a|2|b|2 − (ab)2.
222 Гл. 5. Интегральное исчисление функций многих переменных
В частности, при a = ru, |
b = rv будем иметь |
|
|
2 2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
= |
g11 |
|ru ×rv|2 = rurv − (rurv) |
|
= g11g22 − g12 |
g12 |
|
|
|
|
|
|
|
|
|
|
Формула (46.16) доказана. |
|
|
|
|
|
|
Отметим, что поскольку в неособой точке |
ru = 0 |
то в ней |
|
|
g11 |
g12 |
|
|
|
|
2 |
0, |
|
|
= |ru ×rv|2 > 0, |
g11 = ru > |
g12 |
g22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g12 .
g22
и ru ×rv = 0,
(46.17)
как и должно быть в соответствии с известным из алгебры критерием Сильвестра положительной определенности квадратичной формы.
П р и м е р. Если непрерывно дифференцируемая поверхность имеет явное представление z = f (x, y), (x, y) G, то в силу формул (46.7) и (46.14) получим
g |
= 1 + f 2 |
, g = f f , g = 1 + f 2 |
, |
(46.18) |
11 |
x |
12 |
x y |
22 |
y |
|
|
и потому первая квадратичная форма в этом случае имеет вид |
dr2 = (1 + f 2) dx2 |
+ 2f f dx dy + (1 + f |
2) dy2. |
|
(46.19) |
|
x |
x |
y |
|
y |
|
|
46.4. Длина кривых на поверхности. |
Пусть на непрерыв- |
но дифференцируемой поверхности S = {r(u, v); (u, v) G} задана непрерывно дифференцируемая кривая Γ = {r(u(t), v(t)); a t b} и s = s(t) — переменная длина дуги этой кривой. Мы знаем, что
|
dr |
|
= 1 (п. 17.3), или, что то же самое, |
dr |
= ds . Поэтому в силу |
|
ds |
|
|
|
|
(46.15) |
| | |
| | |
|
формулы |
|
|
|
|
|
ds2 = dr2 = g11 du2 + 2g12 du dv + g22 dv2, |
(46.20) |
где du = u (t) dt, dv = v (t) dt. Таким образом, первая квадратичная форма поверхности равна квадрату дифференциала длины кривой на поверхности.
Если длина дуги s отсчитывается от начала рассматриваемой кри-
вой, т. е. |
ds |
> 0, то из (46.20) получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ds |
= -g11 |
|
|
du |
|
2 |
|
|
du dv |
|
|
dv |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
+ 2g12 |
dt |
|
|
+ g22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
dt |
dt |
dt |
|
|
|
и, следовательно, для длины SΓ кривой Γ имеем формулу |
|
|
|
b |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-g11 |
|
|
|
2 |
|
|
du dv |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
ds |
|
|
|
du |
|
|
|
|
|
|
|
dv |
|
|
SΓ = |
|
|
dt = |
|
|
|
|
+ |
2g12 |
|
|
|
+ g22 |
|
|
|
|
dt. |
|
dt |
|
dt |
dt |
dt |
dt |
aa
46.5.Площадь поверхности. Пусть S = {r(u, v); (u, v) G} —
непрерывно дифференцируемая поверхность, причем G — квадрируемая область на плоскости переменных u, v. Рассмотрим разбиение
Tk этой плоскости на квадраты некоторого ранга k (k фиксировано, k = 0, 1, 2, ...). Обозначим через τ совокупность всех непустых,

§ 46. Элементы теории поверхностей |
223 |
каким-либо образом перенумерованных пересечений замыкания G области G с квадратами ранга k (таких пересечений только конеч-
ное множество). Таким образом, если τ = {Xi}ii==i1τ , то для каждого i = 1, 2, ..., iτ существует такой квадрат Qi Tk, что Xi = G ∩ Qi = .
Ясно, что τ является разбиением множества G и что элементы Xi, этого разбиения являются замкнутыми квадрируемыми множествами (в самом деле, Xi представляет собой пересечение двух замкнутых квадрируемых множеств G и Qi, и поэтому замкнуто).
Пусть τ (∂G) — совокупность тех элементов разбиения τ , которые не пересекаются с границей ∂G области G (см. определение (42.83)
вп. 42.5). Очевидно, что каждое множество Xi τ (∂G) является целым квадратом Qi. Действительно, пусть G ∩ Qi = Xi = Qi; тогда
вквадрате Qi найдется точка, не принадлежащая G. Поскольку же
вквадрате Qi заведомо есть точка из G, ибо G ∩ Qi = , то в нем найдется и точка границы ∂G замыкания G области G (см. замечание 8
вп. 42.1), а поэтому и точка границы ∂G самой области G, так как ∂G ∂G (см. п. 33.33). Это противоречит выбору множества Xi.
Пусть Qi — один из таких квадратов: Qi = Xi τ (∂G), с вершинами Mi = (u, v), (u + h, v), (u + h, v + h), (u, v + h), h > 0, и, следовательно, h — длина его сторон. Тогда
r(u + h, v) − r(u, v) = ruh + o(h),
r(u, v + h) − r(u, v) = rvh + o(h), h → 0.
Обозначим σi площадь параллелограмма, натянутого на векторы ruh и rvh (рис. 45). Имеем
σi = |ruh×rvh| = |ru ×rv|h2 |
|
μXi. |
(46.21) |
= |ru ×rv| Mi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наряду с поверхностью S рассмотрим «чешуйчатую поверхность», состоящую из всех параллелограммов, натянутых на векторы ruh
иrvh, взятые в вершинах Mi = (u, v) квадратов Qi = Xi τ (∂G),
иопределим площадь μS поверхности S как предел суммы площадей
всех указанных параллелограммов, когда мелкость |τ | разбиений τ

224 Гл. 5. Интегральное исчисление функций многих переменных
стремится к нулю: |τ | → 0 (это равносильно тому, что ранг k → +∞).
Таким образом, |
def |
lim |
σ |
. |
(46.22) |
|
μS = |
|τ|→0 Xi τ(∂G) |
i |
|
|
В силу (46.21) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Xi τ(∂G) |
σi = Xi τ(∂G) |ru ×rv| Mi |
μXi. |
Отсюда видно, что эта сумма является неполной интегральной суммой от функции |ru ×rv| на области G, и поскольку μ(∂G) = 0, то (см. теорему 4 в п. 42.5)
lim |
σi = G |ru ×rv| du dv. |
|τ|→0 Xi τ(∂G) |
Интеграл в правой части равенства существует, так как подынтегральная функция |ru ×rv| непрерывна, а следовательно, и интегри-
руема на квадрируемом компакте G, являющемся замыканием области G. Более того, интеграл от этой функции по замыканию G области G совпадает с интегралом от нее по самой области G, ибо G = G ∂G, где граница ∂G имеет меру нуль.
В результате для площади μS поверхности S получилась формула
μS = |
|
|ru ×rv| du dv. |
(46.23) |
|
G |
|
Применив соотношение (46.16), ее можно записать в виде |
|
μS = |
|
|
|
(46.24) |
|
g11g22 − g122 du dv. |
G
Выражение g11g22 − g122 du dv называют иногда элементом пло-
щади поверхности и обозначают его dS, т. е.
dS = g11g22 − g122 du dv. |
(46.25) |
Таким образом,
μS = dS.
G
Пр и м е р. Если поверхность S задана явным представлением z =
=f (x, y), (x, y) G, то в силу формул (46.18) из (46.24) следует, что
μS = 1 + fx2 + fy2 dx dy. (46.26)
G
46.6. Ориентация поверхности. Прежде всего расширим понятие поверхности. В связи с этим поверхности в смысле определения (46.1) будем называть также и элементарными поверхностями.

§ 46. Элементы теории поверхностей |
225 |
Пусть задано конечное множество элементарных поверхностей,
края которых состоят из конечных множеств замкнутых кривых (контуров). Операцией склейки этих поверхностей называется отож-
дествление некоторых дуг этих контуров, при котором (кроме, быть может, конечного множества точек) отождествляются дуги, принадлежащие краям не более чем двух элементарных поверхностей.
Всякий результат склейки элементарных поверхностей называется поверхностью.
П р и м е р 1. Сфера x2 + y2 + z2 = 1 является результатом склейки по окружности x2 + y2 = 1, z = 0, двух элементарных поверхностей
без кратных точек, имеющих явное представление, — полусфер z = |
|
1 − x2 − y2 |
|
= |
и z = − 1 − x2 − y2 , x2 + y2 1. |
П р и м е р 2. |
Если у прямоугольника ABCD (рис. 46) склеить |
отрезки AB и DC, то получится боковая поверхность цилиндра. Если же предварительно «перекрутить» прямоугольник ABCD и склеить уже отрезки AB и CD, то получится
поверхность, называемая листом Мёбиуса. Между двумя получившимися поверхностями имеется большая принципиальная разница: на боковой поверхности цилиндра можно выбрать непре-
рывную единичную нормаль, а на листе Мёбиуса нельзя. У листа Мёбиуса, в отличие от боковой поверхности цилиндра, есть только одна сторона (лист Мёбиуса нельзя покрасить двумя раз-
личными красками так, чтобы две части, окрашенные разными красками, нигде не соприкасались; для боковой поверхности цилиндра это,
очевидно, возможно).
Элементарная гладкая поверхность называется ориентированной,
если на ней задана непрерывная единичная нормаль. Сама эта нормаль называется ориентацией поверхности. Если гладкая поверх-
ность S задана векторным представлением S = {r(u, v); (u, v) G},
|
n = |
ru ×rv |
n. |
то ее ориентацией являются векторы |
|
|ru ×rv | |
и − |
Поверхность S, ориентированная нормалью n, будет обозначаться |
через S+, а нормалью n — через S−. |
|
|
− |
|
|
|
Поверхность, полученная склейкой гладких элементарных поверхностей, называется гладкой, если у каждой точки поверхности найдет-
ся «окрестность», в которой существует единичная нормаль, непрерывная как функция параметров поверхности (в случае когда точка поверхности получена как результат отождествления точек краев элементарных поверхностей, «окрестность» значений параметров точки также образуется путем склейки частей окрестностей значений параметров точки на указанных элементарных поверхностях).
226 Гл. 5. Интегральное исчисление функций многих переменных
Гладкая поверхность называется ориентируемой (двусторонней), если у нее существует единичная нормаль, непрерывная на всей поверхности. Сама эта нормаль называется ориентацией поверхности.
Если у гладкой поверхности нет непрерывной на ней единичной нормали, то поверхность называется неориентируемой (односторонней).
Примером гладкой неориентируемой поверхности, полученной при помощи операции склейки, является лист Мёбиуса.
Результат склейки гладких элементарных поверхностей, краями
которых являются кусочно-гладкие контуры, называется кусочногладкой поверхностью. Ясно, что гладкая поверхность является и ку-
сочно-гладкой.
Примером кусочно-гладкой поверхности, не являющейся гладкой, является поверхность куба, получающаяся, очевидно, cклейкой его граней (гладких поверхностей) по их ребрам. Ясно, что на поверхности куба нет непрерывной единичной нормали, в точках ребер она даже не существует. Поэтому для кусочно-гладких поверхностей определение их ориентируемости вводится другим путем.
Рассмотрим сначала гладкую элементарную поверхность, краем которой является простой замкнутый контур. Его ориентация называется согласованной с ориентацией самой поверхности (т. е. с непрерывной единичной нормалью), если они согласованы по правилу штопора
вслучае правой системы координат и по правилу антиштопора —
вслучае левой системы координат.
Конечно, следует отдавать себе отчет в том, что, как и в случае плоскости (см. п. 45.5), понятие правой и левой системы координат, а также правила штопора и антиштопора не являются математическими. Они употребляются для наглядности и часто удобны для конкретных приложений теории поверхностей.
Понятие ориентации края поверхности, согласованной с ориентацией самой поверхности при фиксированной системе координат, можно определить и чисто математически, 
 но, чтобы не усложнять изложение, мы не будем
но, чтобы не усложнять изложение, мы не будем
на этом останавливаться. Там, где эти понятия
будут встречаться, они будут конкретно описы-
ваться (например, в теореме Стокса, см. п. 48.4).
Кусочно-гладкая поверхность называется
ориентируемой (двусторонней), если у элементарных гладких поверхностей, из которых она получена с помощью склейки, имеются
 такие ориентации, что согласованные с ними ориентации частей их краев, принадлежащих двум указанным
такие ориентации, что согласованные с ними ориентации частей их краев, принадлежащих двум указанным
элементарным поверхностям, противоположны (рис. 47). Если это невозможно для данной поверхности, то она называется неориентируемой (односторонней).
§ 46. Элементы теории поверхностей |
227 |
Можно показать, что в случае, когда кусочно-гладкая поверхность является гладкой, два данных определения ее ориентации (с помощью непрерывной на ней единичной нормали и с помощью согласованных ориентаций составляющих ее элементарных поверхностей с ориентациями их краев) равносильны. Можно также показать, что как бы ни разбивать лист Мёбиуса на гладкие части, краями которых являются простые замкнутые контуры, эти контуры нельзя согласованно ориентировать. Таким образом, и в этом смысле лист Мёбиуса является неориентируемой по- 
верхностью. Если носитель поверхности S является гра-
ницей некоторой области в трехмерном пространстве, то нормаль к этой поверхности (там,
где она, конечно, существует), направленная внутрь области, называется внутренней, а на-
правленная вовне от области — внешней. Если эта поверхность S является кусочно-гладкой,
то она ориентируема, и ее внешняя и внутренняя единичные нормали являются ориентация-
ми. Это наглядно видно на примере поверхно-
сти куба. Области, границы которых представляют собой кусочногладкую поверхность, называются областями с кусочно-гладкой границей.
П р и м е р 3. Если гладкая поверхность S имеет явное представ-
ление z = f (x, y), (x, y) G, |
то в силу формул (46.7) будем иметь |
|
|
rx ×ry = |
|
i |
j k |
|
= −fx i + fy j + k. |
|
|
|
|
|
|
1 0 fx |
|
(46.27) |
|
|
|
|
|
0 |
1 fy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда следует, что вектор |
|
|
|
|
|
|
|
|
|
|
|
|
n = |
rx ×ry |
= |
|
|
|
fx |
|
|
|
|
|
|
|
|
|
fy |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|rx ×ry | |
'− |
1 + fx2 + fy2 |
|
− |
1 + fx2 + fy2 |
|
1 + fx2 |
(46.28) |
|
|
|
|
|
|
+ fy2 ( |
является ориентацией поверхности S (рис. 48). При этом |
|
|
|
|
|
|
cos nk, = |
|
|
|
|
|
1 |
|
|
|
> 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+ fx2 + fy2
т.е. ориентация n образует острый угол с осью z. Это означает, что вектор n направлен вверх от поверхности S. Поэтому поверхность S,
ориентированная единичной нормалью n, называется «верхней сторо-
|
поверхности S, а ориентированная противоположной |
норма- |
ной» S |
лью −n (направленной вниз) — ее «нижней стороной» S. |
|
Обратим внимание на то, что если граница ∂G области G является простым замкнутым контуром, то его положительная ориентация

228 Гл. 5. Интегральное исчисление функций многих переменных
на плоскости переменных x, y, на которой выбрана правая система координат, а следовательно, и порожденная ей ориентация края ∂S поверхности S, согласованы с нормалью n «по правилу штопора».
§47. Поверхностные интегралы
47.1.Определения поверхностных интегралов. Пусть
S = {r(u, v); (u, v) |
G |
} |
(47.1) |
— поверхность, G — квадрируемая область, r(u, v) — непрерывно дифференцируемая в ее замыкании G векторная функция, g11, g12 и g22 — коэффициенты первой квадратичной формы поверхности S, F — функция, заданная на поверхности S, т. е. F = F (r(u, v)) = = F (x(u, v), y(u, v), z(u, v)), (u, v) G.
Интегралом первого рода F ds по поверхности S называется
интеграл |
|
S |
|
|
|
|
|
def |
|
F (x(u, v), y(u, v), z(u, v)) g11g22 − g122 du dv |
S F (x, y, z) dS = |
G |
|
|
(47.2) |
(под dS понимается элемент площади поверхности S; см. (46.25)). Если подынтегральная функция в интеграле правой части ра-
венства (47.2) непрерывна на замыкании G области G (т. е. если функция F непрерывна на поверхности S), то поверхностный ин-
теграл F dS существует как интеграл от непрерывной функции
S |
g11g22 − g122 непрерывна |
по квадрируемому компакту G (функция |
на множестве G в силу непрерывной дифференцируемости на нем векторной функции r(u, v)). Напомним, что интегралы по области G и ее замыканию G совпадают (см. п. 42.3).
П р и м е р 1. Если F ≡ 1 на поверхности S, то поверхностный
интеграл (47.2) равен площади поверхности S:
dS = g11g22 − g122 du dv = μS.
SG
П р и м е р 2. Если поверхность S задана явным представлением
|
|
|
|
|
z = f (x, y), (x, y) |
G |
, то |
(см (46.26)) |
S |
F (x, y, z) dS = |
G F (x, y, f (x, y)) 1 + fx2 + fy2 dx dy. |
Поверхностный интеграл первого рода по кусочно-гладкой поверхности определяется как сумма интегралов по ее гладким частям.
§ 47. Поверхностные интегралы |
229 |
Пусть теперь S — гладкая поверхность и |
|
n = (cos α, cos β, cos γ) |
(47.3) |
— непрерывная единичная нормаль на ней. Ориентированную с помощью этой нормали поверхность обозначим S+. Пусть, далее, a = = a(r(u, v)) — непрерывная векторная функция, заданная на поверхности S, и P , Q, R — координаты вектора a, т. е.
|
a = (P , Q, R). |
(47.4) |
Таким образом, P , Q, R являются непрерывными числовыми |
функциями на поверхности S: |
|
|
|
|
P = P (r(u, v)), |
Q = Q(r(u, v)), R = R(r(u, v)), (u, v) |
|
|
G. |
Поверхностным интегралом |
a dS второго рода по ориентиро- |
|
S+ |
|
|
|
|
ванной поверхности S+ называется интеграл |
an dS, т. е. |
|
|
|
S |
|
def |
an dS. |
(47.5) |
|
a dS = |
|
S+ |
S |
|
|
|
Обозначение |
a dS называется векторной записью поверхност- |
S+
ного интеграла второго рода. Его координатной записью называется выражение
P dy dz + Q dz dx + R dx dy.
S+
Таким образом, |
|
|
a dS = |
P dy dz + Q dz dx + R dx dy, |
(47.6) |
S+ |
S+ |
|
так как по определению левая и правая части этого равенства являются разными записями одной и той же величины.
Записав скалярное произведение an в координатном виде:
an = P cos α + Q cos β + R cos γ,
(47.3) (47.4)
получим |
|
P dy dz + Q dz dx + R dx dy = |
a dS = |
(47.6) |
(47.5) |
S+ |
S+ |
=an dS = (P cos α + Q cos β + R cos γ) dS. (47.7)
(47.5)








 но, чтобы не усложнять изложение, мы не будем
но, чтобы не усложнять изложение, мы не будем такие ориентации, что согласованные с ними ориентации частей их краев, принадлежащих двум указанным
такие ориентации, что согласованные с ними ориентации частей их краев, принадлежащих двум указанным