53

3. Операторный метод расчета переходных процессов

3.1. Введение к операторному методу

Операторный метод основан на использовании понятия об изображении функций времени. В операторном методе каждой функции времени соответствует функция новой переменной, обозначаемой буквой р, и наоборот— функции переменной р отвечает определенная функция времени.

Переход от функции времени к функции от р осуществляют с помощью прямого преобразования Лапласа.

Таким образом, операторный метод расчета переходных процессов представляет собой метод расчета, основанный на преобразовании Лапласа.

Операторный метод позволяет свести операцию дифференцирования к умножению, а операцию интегрирования — к делению. Это облегчает интегрирование дифференциальных уравнений.

В операторном методе расчет делится на две части:

1. Осуществляют переход в область изображений (оригинал переводят в изображение не как в фотографии, а преобразование). С помощью преобразования Лапласа дифференциальные уравнения переходных процессов удается заменить алгебраическими;

2. Находят решения в операторной области и осуществляют возврат в область оригинала. В общем случае обратное преобразование осуществляют с помощью интеграла Бромвича. В электрических задачах этим интегралом не пользуются, а применяют теоремуразложенияилиинтеграл сверток.

Здесь:

Оригинал– это любая функция или параметр цепи в области времени.

Изображение – это преобразованный оригинал с помощью интеграла Лапласа.

р- оператор Лапласа (в общем случае может быть комплексным числом).

Интеграл прямого преобразования Лапласа имеет вид:

.

Если есть оригинал f(t), от которого можно взять интеграл Лапласа, то ему соответствует изображениеF(p).

3.2. Изображения по Лапласу основных электрических величин, используемых при расчетах переходных процессов

Изображение по Лапласу оригинала в виде постоянной во времени величины

Пусть оригинал является постоянной величиной f(t)=U₀ =const. Вычислим интеграл Лапласа:.

Постоянной величине в области изображения соответствует эта же постоянная, делённая на оператор «р».

Не всегда размерность оригинала соответствует размерности изображения.

Существует такое преобразование, аналогичное преобразованию Лапласа, в котором совпадают размерности – это преобразование Карсона: C(p)=pF(p).

Преобразование Карсона здесь рассматривать не будем.

Изображение показательной функции

Если , то изображение:

Таким образом: .

Отсюда вытекает ряд важных следствий. Положив =j, получим

Функции е^tсоответствует изображение:

Если функция времени представляет собой синусоидальную величину, например, ЭДС , тоE(p), при, равно:

.

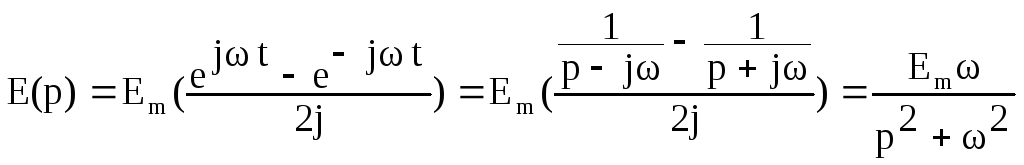Изображение по Лапласу комплексной величины

Пусть, тогда, и функция времени может быть выражена через комплекс напряжения. Подвергнем вращающийся комплекс преобразованию Лапласа:.

Изображение по Лапласу производной функции времени

Известно, что функ­ции f(t) соответствует изображение F(р). Требуется найти изображение первой производной, если известно, что значение функцииf (t)приt=0равно f(0).

Подвергнем функцию преобразованию Лапласа:

Интегрирование произведем по частям. Обозначив и,

Имеем:

Следовательно, .

Но a

Таким образом,

Изображение напряжения на индуктивности

Исходить будем из условия, что оригиналу тока i соответствует изображение тока I(р). Запишем оригинал напряжения на индуктив­ности:

По формуле определим изображение производной тока:

где t (0)- значение тока i при t=0.

Следовательно, . Если i(0)=0, то

Изображение второй производной

Следовательно, изображение второй производной тока i.

Изображение интеграла функции времени

Требуется найти изображение функции , если известно, что изображение функции f(t) равно F(р).

Подвергнем функцию преобразованию Лапласа:

и возьмем интеграл по частям:

Первое слагаемое правой части при подстановке и верхнего и ниж­него пределов дает нуль. При подстановке верхнего предела нуль получается за счет ранее наложенного ограничения на функцию f(t): функцияf(t)если и растет с увеличениемt, то все же медленнее, чем растет функцияе^at, гдеа– действительная частьр. При подстановке нижнего предела нуль получается за счет обращения в нуль. Следовательно, еслито

Изображение напряжения на конденсаторе

Напряжение на конденсаторе часто записывают в виде, где не

указаны пределы интегрирования по времени. Более полной является следующая запись: где учтено, что к моменту времени t напряжение на конденсаторе определяется не только током, протекавшим через конденсатор в интер­вале времени от 0 до t, но и тем напряжениемкоторое на нем было при t=0. В соответствии с формулой Лапласа изображениеравно, а изображение постояннойесть постоянная, деленная на р. Поэтому изображение напряжения на конденсаторе запи­сывают следующим образом:

Оригинал.	Изображение
f(t)	F(p)
i(t)	I(p)
U0
	pF(р) – f(0)
	LpI(p) – Li(0_ )
Emsin(wt)

Сведем все преобразования в таблицу.