15. Теорема Коши-Пикара для ду-1-проп. Доказательство сходимости пикаровских приближений к непрерывной функции.

- уравнение (1).- задача Коши (2)

Теорема Коши-Пикара:пусть дано (1) и поставлена задача Коши (2). Если в областиудовлетворяет условиям: 1) определена и непрерывна по совокупности переменных; 2) условие Липшица, то задача Коши имеет единственное решение, определенное, непрерывное, непрерывно дифференцируемое, по крайней мере, в окрестности,, где,.

Доказательство:

Утверждение 3:присуществует, и- непрерывная функция.

Доказательство:приимеем функциональный ряд, причем. Если доказать, сходимостьк, то будет доказано и утверждение.

Оценим: ,

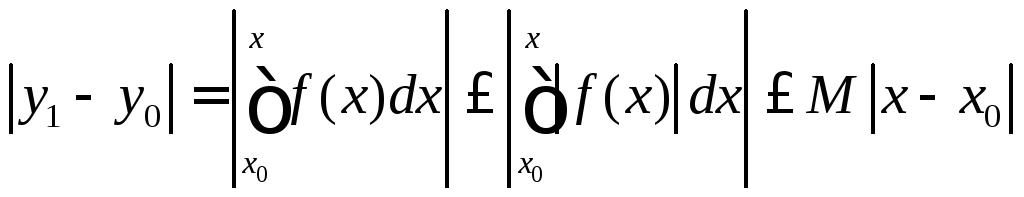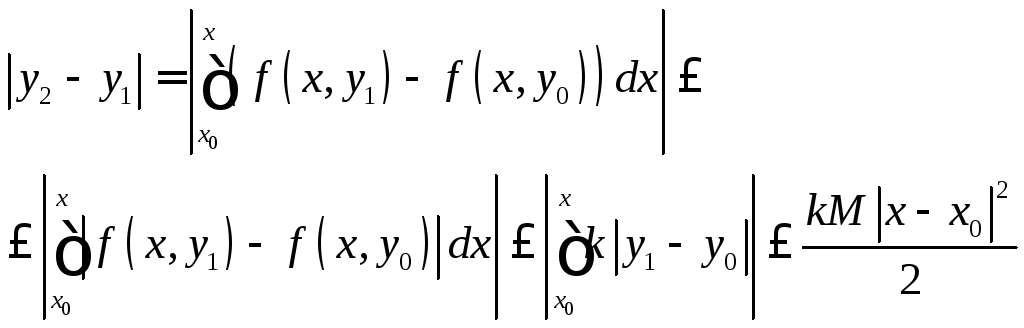
Предположим, что и докажем, что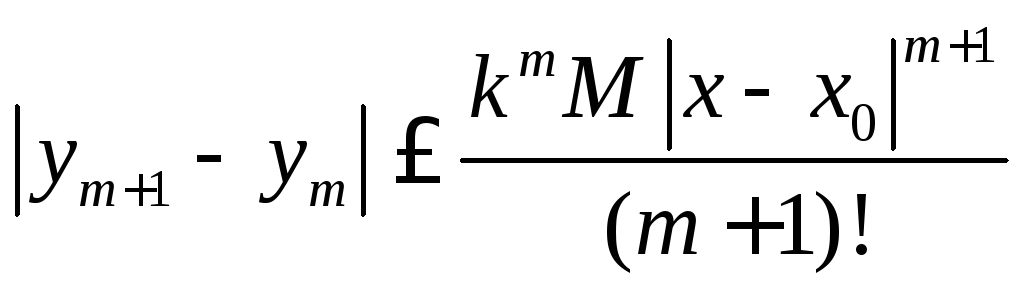

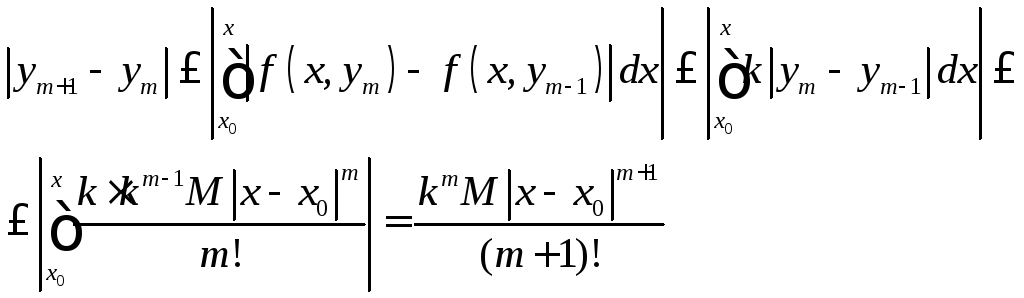, т.к., тогда каждый член ряда по модуля меньше соответствующего элемента числового ряда, он сходится по признаку Даламбера:. Таким образом,сходится равномерно по признаку Вейерштрасса для любого. Каждый член ряда непрерывная функция, следовательно,также непрерывна.

16. Теорема Коши-Пикара для ду-1-проп. Доказательство сходимости пикаровских приближений к решению задачи Коши.

- уравнение (1).- задача Коши (2)

Теорема Коши-Пикара:пусть дано (1) и поставлена задача Коши (2). Если в областиудовлетворяет условиям: 1) определена и непрерывна по совокупности переменных; 2) условие Липшица, то задача Коши имеет единственное решение, определенное, непрерывное, непрерывно дифференцируемое, по крайней мере, в окрестности,, где,.

Доказательство:

Утверждение 4:- решение задачи Коши (2) для уравнения (1).

Доказательство: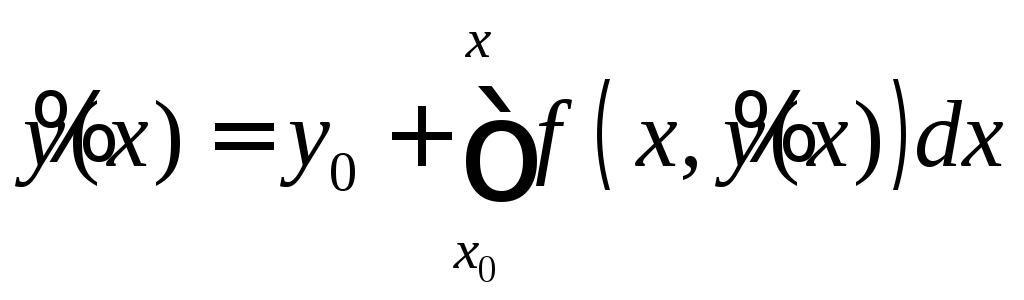

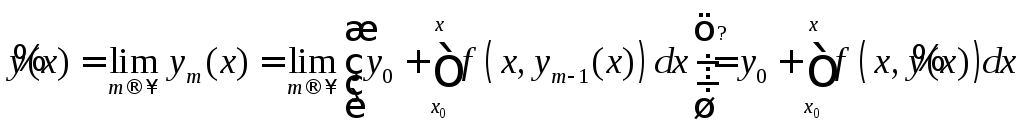. Таким образом, надо доказать, что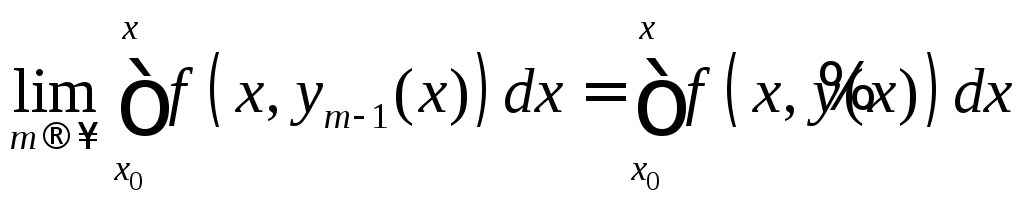. Выпишем достаточное условие сходимости: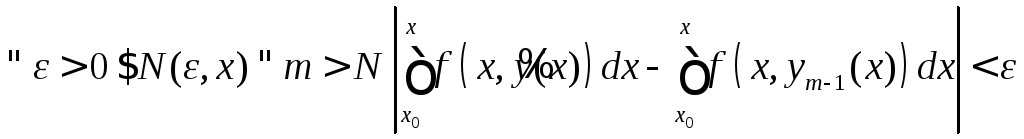

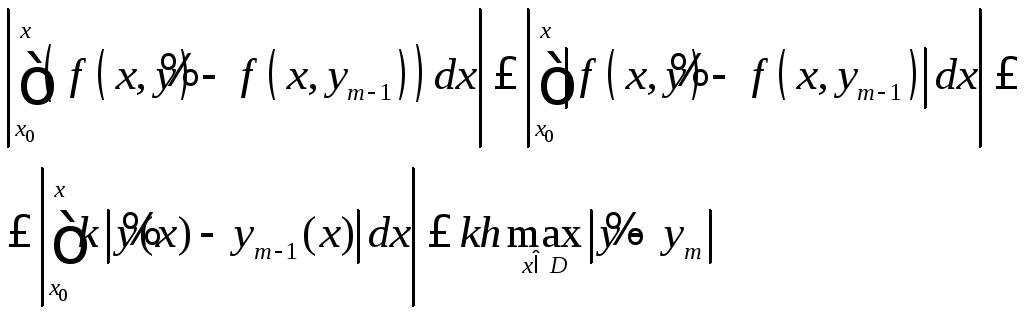
Условие равномерной сходимости :

, тогдаи оба неравенства выполняются.

17. Теорема Коши-Пикара для ду-1-проп. Доказательство единственности решения. Метод Пикара как приближенный метод решения задачи Коши.

- уравнение (1).- задача Коши (2)

Теорема Коши-Пикара:пусть дано (1) и поставлена задача Коши (2). Если в областиудовлетворяет условиям: 1) определена и непрерывна по совокупности переменных; 2) условие Липшица, то задача Коши имеет единственное решение, определенное, непрерывное, непрерывно дифференцируемое, по крайней мере, в окрестности,, где,.

Доказательство:

Утверждение 5:- единственное решение задачи Коши (2) для уравнения (1)

Доказательство:пусть существует,ив подынтервале.

, однако, в то же время это равно:

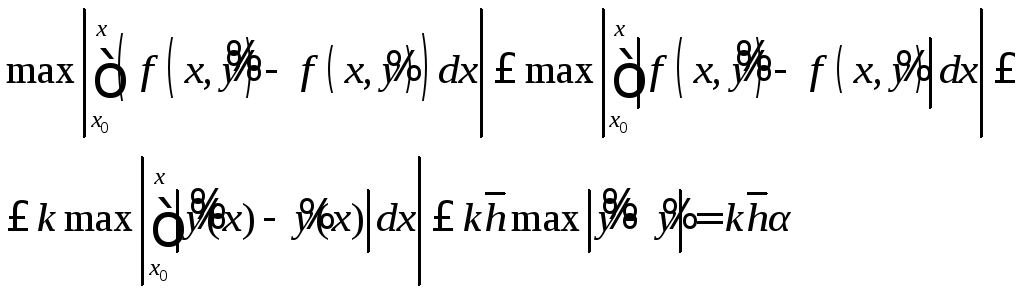
Таким образом , значит,. Т.к.- любое число, положим егои тогда предположение неверно.

Метод Пикара как приближенный метод решения задачи Коши.

Последовательность пикаровых приближений равномерно сходится к точному решению. Насколько хорошо-ое приближение аппроксимирует точное решение?

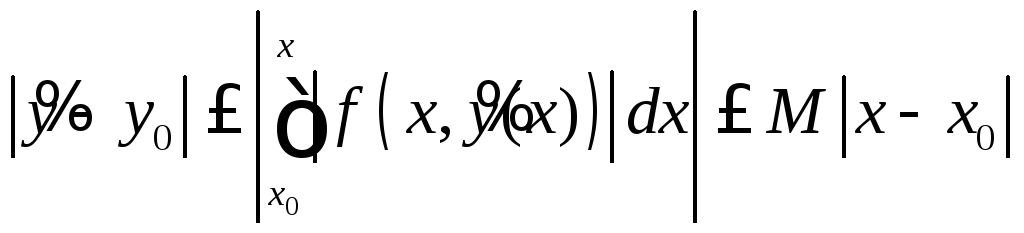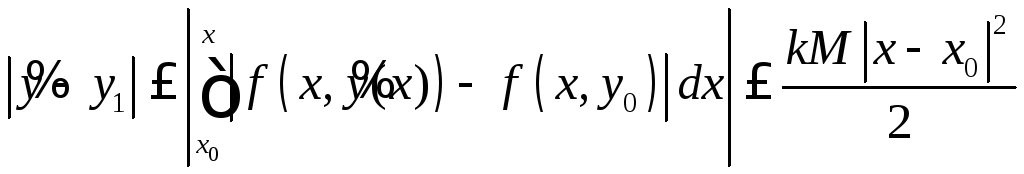,. Методом матиндукции можно показать, что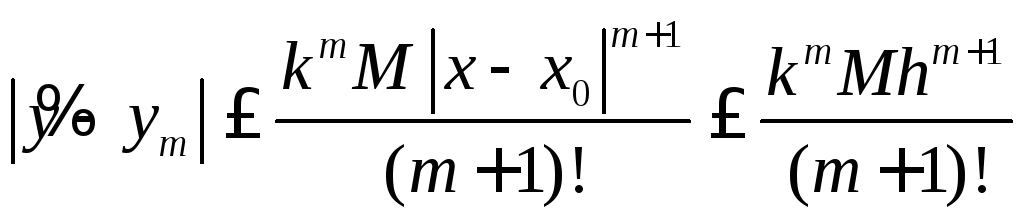

18. Теорема о продолжении решения задачи Коши. Продолжаемые и непродолжаемые решения.

В теореме Коши-Пикара доказано существование и единственность решения задачи Коши на . Если, то вокруг этой точки можно построить прямоугольник, в котором будут выполняться условия теоремы Коши-Пикара. Необходимо получить единственное решениена, причем, следовательно, по теореме Коши-Пикара они будут совпадать на отрезке.

Решение - продолжение решения. Аналогичные рассуждения проводятся, пока не получаем точку на границе.

Решение, продолжаемое вправо и/или влево – продолжаемое. Решение, не продолжаемое ни вправо, ни влево –непродолжаемое.

Теорема:при выполнении теоремы Коши-Пикара в ограниченной замкнутой областирешениепродолжаемо до границы.

Теорема:еслиопределена и непрерывна ви удовлетворяет условию Липшица во всякой ограниченной области этой плоскости, то всякая ИК неограниченно продолжаема доили имеет вертикальную асимптоту при конечном.

Таким образом, ИК может быть непродолжаемой ввиду приближения к точке нарушения условий Коши-Пикара или ввиду приближения к асимптоте.