
- •1. Основные понятия о ду.
- •2. Ду-1-проп. Решение. Общее решение, частное решение. Общий интеграл. Задача Коши. Существование и единственность решения задачи Коши.
- •3. Геометрическая интерпретация ду-1-проп. Поле направлений. Интегральная кривая. Геометрический смысл задачи Коши. Обыкновенная и особые точки.
- •4. Качественное исследование ду-1-проп. Изоклины. Линия экстремумов и линия перегибов интегральных кривых.
- •5. Особые решения ду-1-проп. Способы их отыскания.
- •6. Ду 1 порядка с разделяющимися переменными и приводимые к ним.
- •8. Ду 1 порядка, приводимые к однородным.
- •9. Линейные ду 1 порядка. Структура общего решения. Метод вариации произвольной постоянной.
- •10. Ду 1 порядка, приводимые к линейным. Ду Бернулли и Риккати
- •11. Ду 1 порядка в полных дифференциалах.
- •12. Интегрирующий множитель ду 1 порядка. Способы его нахождения. Связь с особыми решениями. Число интегрирующих множителей данного уравнения
- •13. Интегрирующий множитель для ду с разделяющимися переменными, однородного и линейного.
- •14. Теорема Коши-Пикара для ду-1-проп. Метод последовательных приближений Пикара построения решения.
- •15. Теорема Коши-Пикара для ду-1-проп. Доказательство сходимости пикаровских приближений к непрерывной функции.
- •16. Теорема Коши-Пикара для ду-1-проп. Доказательство сходимости пикаровских приближений к решению задачи Коши.
- •17. Теорема Коши-Пикара для ду-1-проп. Доказательство единственности решения. Метод Пикара как приближенный метод решения задачи Коши.
- •18. Теорема о продолжении решения задачи Коши. Продолжаемые и непродолжаемые решения.
- •19. Теорема о непрерывной зависимости решения задачи Коши от параметров.
- •20. Теорема о непрерывной зависимости решения задачи Коши от начальных условий.
- •21. Степень гладкости решения задачи Коши. Дифференцируемость решения по начальным данным и параметрам.
- •22. Численные методы интегрирования ду 1 порядка. Методы I и II порядка. Одношаговые и многошаговые методы. Особенности численного моделирования решения ду.
- •23. Ду-1-пнроп. Решение. Общее решение, частное решение. Общий интеграл. Поле направлений. Постановка задачи Коши.
- •24. Теорема Коши-Пикара для ду 1 порядка, не разрешенного относительно производной.
- •25. Особые решения ду-1-нпроп. Способы отыскания. Дискриминантная кривая. Огибающая семейства интегральных кривых.
- •26. Методы интегрирования ду-1-пнроп. Уравнения, не содержащие искомой функции.
- •27. Методы интегрирования ду-1-пнроп. Уравнения, не содержащие независимой переменной.
- •28. Методы интегрирования ду-1-пнроп. Общий случай.
- •29. Ду Лагранжа
- •30. Ду Клеро
11. Ду 1 порядка в полных дифференциалах.
![]() - уравнение в полных дифференциалах,
если
- уравнение в полных дифференциалах,
если![]() .
.
Теорема:пусть![]() и
и![]() определены в односвязной области
определены в односвязной области![]() плоскости
плоскости![]() ,
одновременно не обращаются в 0 и имеют
непрерывные частные производные по
обеим переменным, а также
,
одновременно не обращаются в 0 и имеют
непрерывные частные производные по
обеим переменным, а также![]() .
Тогда общий интеграл имеет вид
.
Тогда общий интеграл имеет вид![]() и задача Коши имеет единственное решение.
и задача Коши имеет единственное решение.
Доказательство:если![]() ,
то
,
то![]() ,
,![]() ,
значит,
,
значит,![]() и
и![]() .
Значит,
.
Значит,![]() - общее решение. Если поставлена задача
Коши
- общее решение. Если поставлена задача
Коши![]() ,
то
,
то![]() и
и![]() .
.
Аналогично для
![]()
![]() .
.
Теорема:чтобы уравнение![]() при наложенных на
при наложенных на![]() и
и![]() ограничениях было уравнением в полных
дифференциалах необходимо и достаточно
выполнения
ограничениях было уравнением в полных
дифференциалах необходимо и достаточно
выполнения![]() .
.
Доказательство:1) необходимость
Пусть существует такая
![]() ,
что
,
что![]() .
.![]() и
и![]() непрерывны. Продифференцируем их по
непрерывны. Продифференцируем их по![]() и
и![]() соответственно:
соответственно:![]() ,
,![]() .
Смешанные производные непрерывны,
значит, равны и необходимость доказана.
.
Смешанные производные непрерывны,
значит, равны и необходимость доказана.
2) достаточность
Найдем такую
![]() ,
что
,
что![]() .
.![]() .
Найдем производную по
.
Найдем производную по![]() .
.
![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() .
.
12. Интегрирующий множитель ду 1 порядка. Способы его нахождения. Связь с особыми решениями. Число интегрирующих множителей данного уравнения
Пусть
![]() не является уравнением в полных
дифференциалах.
не является уравнением в полных
дифференциалах.
Интегрирующий множитель–
функция![]() ,
после умножения на которую, уравнение
становится УВПД.
,
после умножения на которую, уравнение
становится УВПД.![]() - непрерывно дифференцируема.
- непрерывно дифференцируема.
Общий интеграл может содержать постороннее
решение
![]() .
В процессе решения может быть потеряно
решение
.
В процессе решения может быть потеряно
решение![]() .
.
Будем искать
![]() в виде
в виде![]() ,
где
,
где![]() - заданная функция.
- заданная функция.![]() ,
тогда
,
тогда![]() ,
,![]() .
.![]() ,
,![]() ,
,![]() ,
,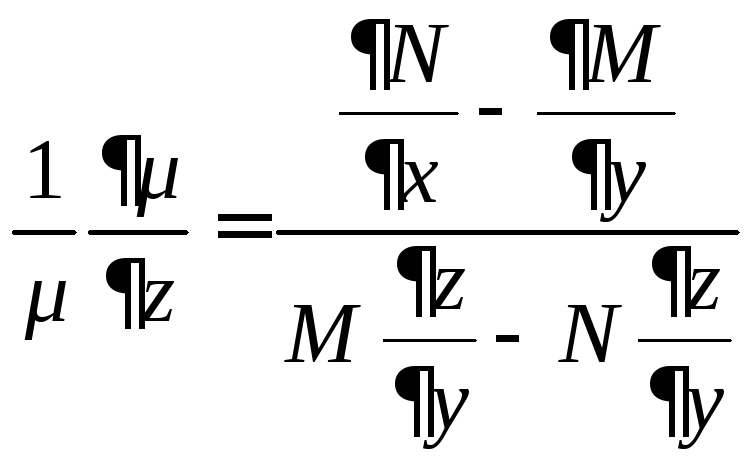 ,
,![]() ,
,![]()
Теорема:если![]() в области
в области![]() плоскости
плоскости![]() имеет общий интеграл, то оно имеет
интегрирующий множитель.
имеет общий интеграл, то оно имеет
интегрирующий множитель.
Доказательство:![]() ,
,![]() ,
,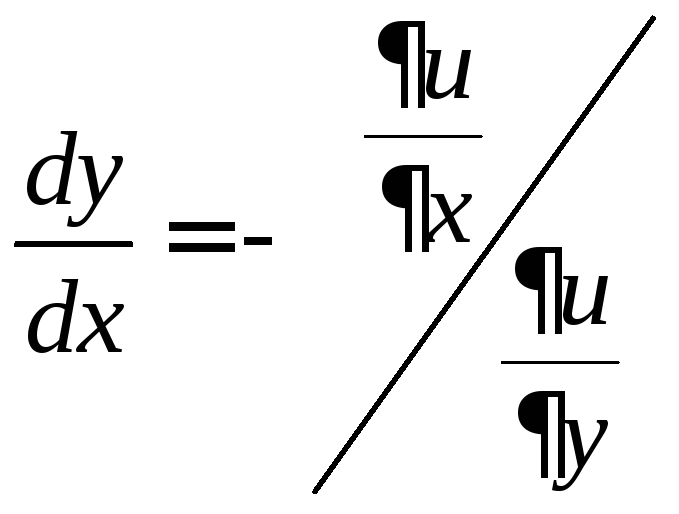 ,
,![]() ,
,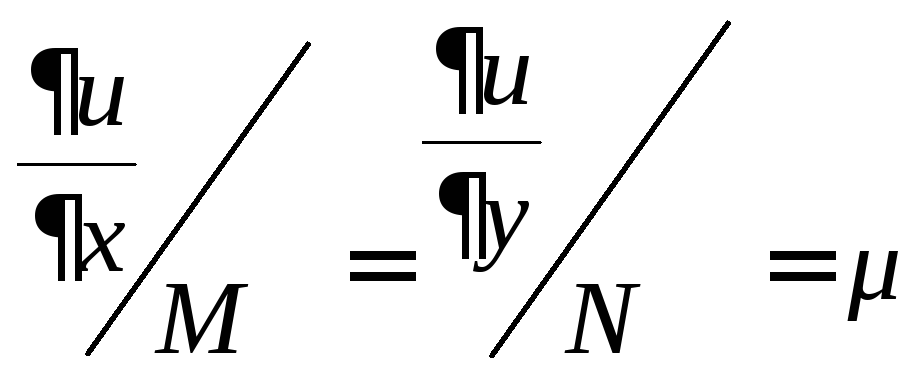 .
.
Теорема:пусть![]() ,
в котором
,
в котором![]() и
и![]() непрерывны и непрерывно дифференцируемы
в области
непрерывны и непрерывно дифференцируемы
в области![]() имеют интегрирующий множитель
имеют интегрирующий множитель![]() ,
т.е.
,
т.е.![]() .
Тогда
.
Тогда![]() - тоже интегрирующий множитель.
- тоже интегрирующий множитель.
Следствие:![]() имеет бесконечно много интегрирующих
множителей.
имеет бесконечно много интегрирующих
множителей.
13. Интегрирующий множитель для ду с разделяющимися переменными, однородного и линейного.
Интегрирующий множитель–
функция![]() ,
после умножения на которую, уравнение
становится УВПД.
,
после умножения на которую, уравнение
становится УВПД.![]() - непрерывно дифференцируема.
- непрерывно дифференцируема.
Общий интеграл может содержать постороннее
решение
![]() .
В процессе решения может быть потеряно
решение
.
В процессе решения может быть потеряно
решение![]() .
.
Интегрирующий множитель для уравнения
с разделяющимися переменными:
![]()
Интегрирующий множитель для однородного
уравнения:
![]()
Интегрирующий множитель для линейного
уравнения:
![]()
14. Теорема Коши-Пикара для ду-1-проп. Метод последовательных приближений Пикара построения решения.
![]() - уравнение (1).
- уравнение (1).![]() - задача Коши (2)
- задача Коши (2)
Теорема Коши-Пикара:пусть дано
(1) и поставлена задача Коши (2). Если в
области![]()
![]() удовлетворяет условиям: 1) определена
и непрерывна по совокупности переменных;
2) условие Липшица
удовлетворяет условиям: 1) определена
и непрерывна по совокупности переменных;
2) условие Липшица![]() ,
то задача Коши имеет единственное
решение, определенное, непрерывное,
непрерывно дифференцируемое, по крайней
мере, в окрестности,
,
то задача Коши имеет единственное
решение, определенное, непрерывное,
непрерывно дифференцируемое, по крайней
мере, в окрестности,![]() ,
где
,
где![]() ,
,![]() .
.
Доказательство:
Сведение задачи Коши к интегральному уравнению
Утверждение 1:задача Коши (2) для
уравнения (1) эквивалентна интегральному
уравнению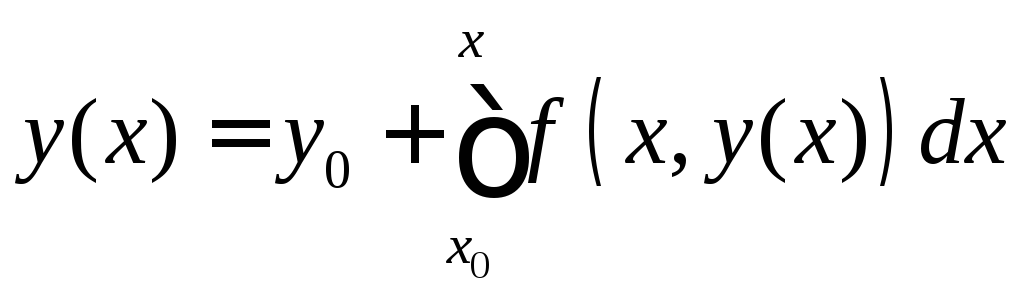 (3)
(3)
Доказательство:пусть для (1)
задача Коши (2) решена, т.е.![]() .
Проинтегрируем:
.
Проинтегрируем: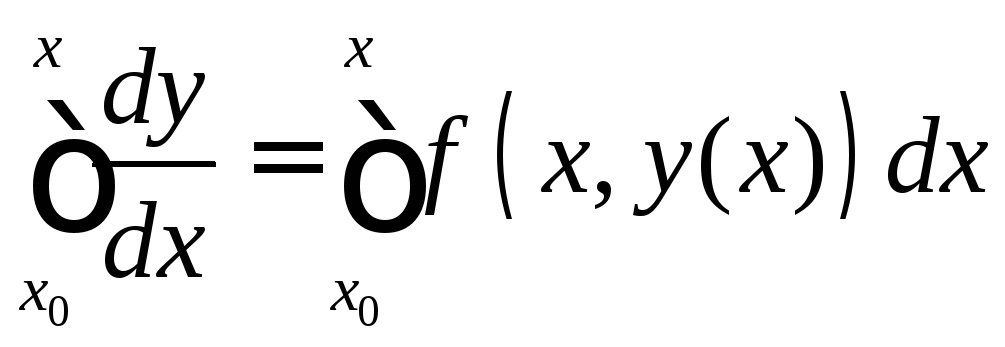 .
.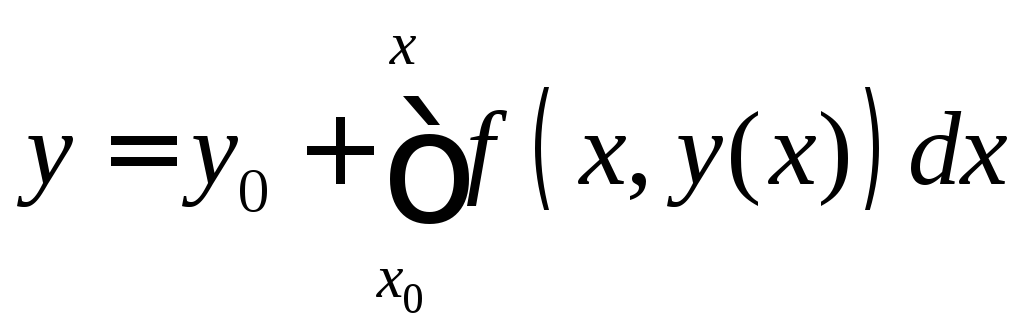 .
Пусть
.
Пусть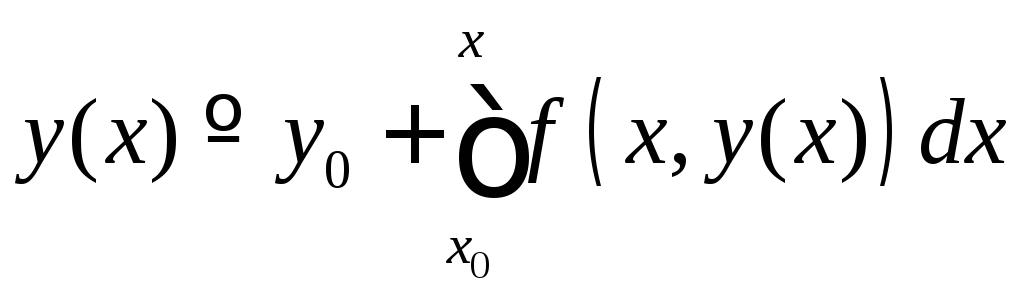 .
Продифференцируем:
.
Продифференцируем:![]() ,
,![]() .
.
Следствие:если![]() ,
то любое решение (3) находится внутри
области
,
то любое решение (3) находится внутри
области![]() .
.
Доказательство: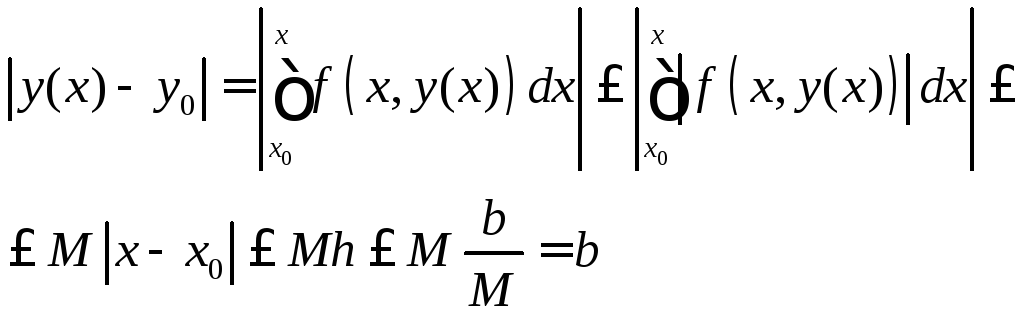
Метод последовательных приближений Пикара.
Построение решения (3).
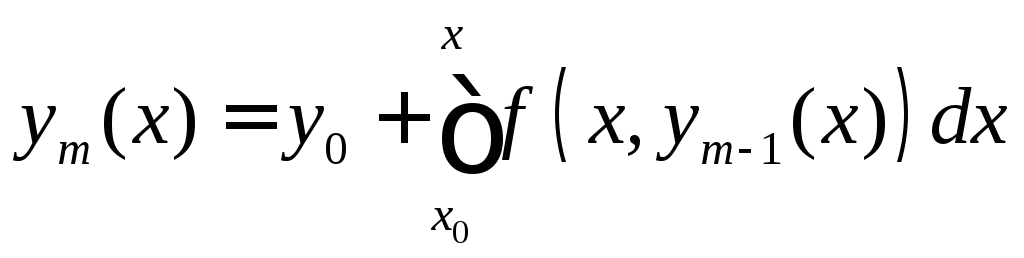 (4).
(4).
Утверждение 2:на интервале![]() любое пикарово приближение определено,
непрерывно и находится внутри
любое пикарово приближение определено,
непрерывно и находится внутри![]() ,
т.е.
,
т.е.![]()
Доказательство: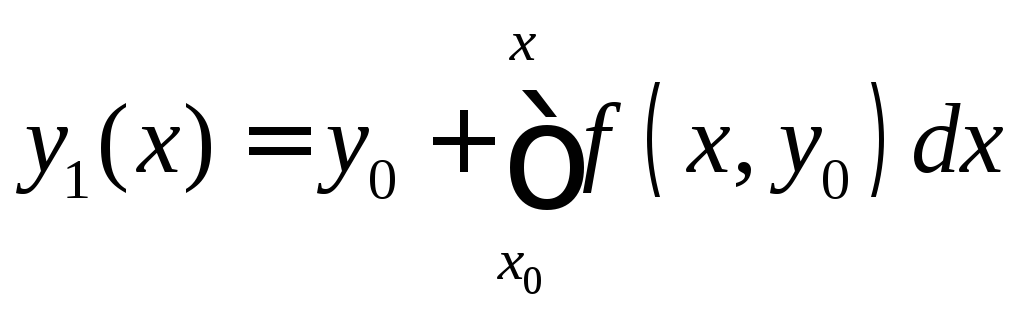 определено и непрерывно, т.к.
определено и непрерывно, т.к.![]() определена и непрерывна.
определена и непрерывна.
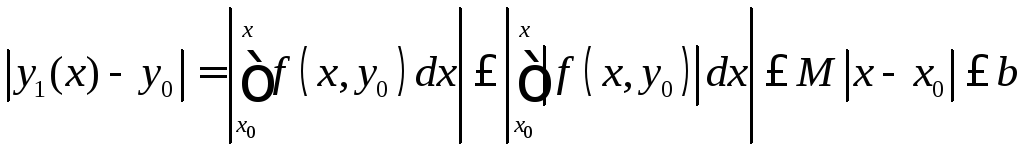 .
Пусть это верно для
.
Пусть это верно для![]() -го,
докажем для
-го,
докажем для![]() -го.
-го.
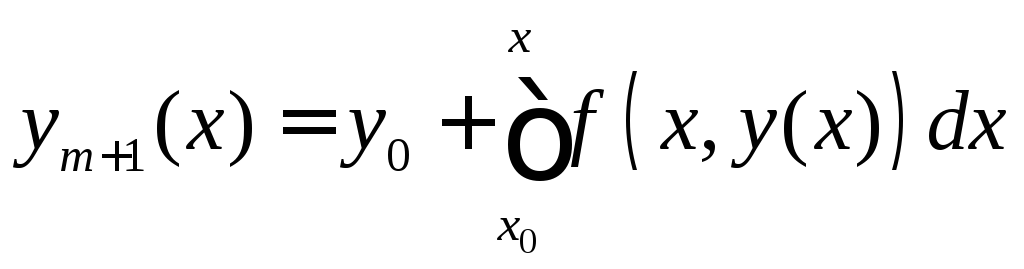 .
Т.к.
.
Т.к.![]() ,
а
,
а![]() ,
то
,
то![]() определена и непрерывна в
определена и непрерывна в![]() ,
значит, интеграл определен и непрерывен,
также, как и
,
значит, интеграл определен и непрерывен,
также, как и![]() -е
приближение.
-е
приближение.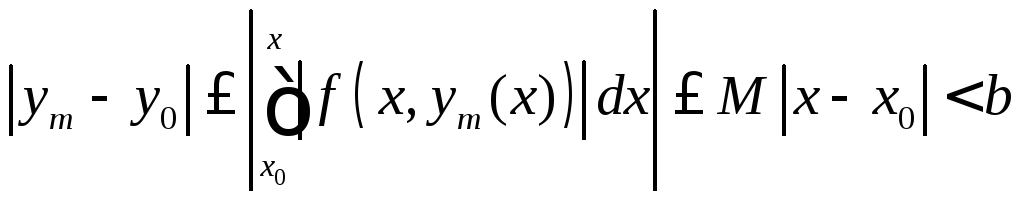 .
.
