
- •3. Визначники 2–го порядку та їх властивості.
- •Доведення:
- •6Означення визначника n-го порядку
- •7Властивості визначників n-го порядку
- •8Поняття вектора.Лінійні дії над векторами.
- •11 Декартова система координат
- •12Скалярний добуток векторів
- •13Векторний добуток векторів
- •14. Мішаний добуток трьох векторів.
- •21. Взаємне розташув 2 площ. Кут між прямою і площиною
- •22. Канонічне рівняння еліпса, його геометричні властивості.
- •27 Множення матриць
- •28 Елементарні перетворення матриць
- •32. Компл числа. Тригонометрична форма комплексного числа
- •33. Дії над компл. Числами. Ф-ла Муавра
- •34. Операції над многочленами.
- •35. Корені многочленів. Теорема Безу. Метод Горнера
- •36 Основна теорема алгебри
- •37. Раціональні дроби
- •38.Аксіоматичне визначення векторного простору
- •40.Підпростори векторного простору
- •41.Афінний простір...
- •42.Ранг матриці.
- •43.Підпр, утвор ровязк однор слр
- •44 Неоднор системи лінійних рівнянь. Теорема Кронекера-Капеллі
- •45.Лп та їх матриці. Дії над лп. Обернене лп.
- •46.Матриці лп. Подібні матриці.
- •47.Характеристичний многочл, власні числа і власні вектори лп
- •48. Означ евклід прост. Ортог вектори. Ортогоналізація Гр-Шмі.
- •49.Ортонормовані базиси і ортогональні матриці.
- •50.Ортогональні перетворення.
- •51 Означення квадратичних форм(кф). Основні ознаки додатної визначеності.
- •52 Зведення кф до канонічного вигляду
- •53) Поняття множини. Рівність множин.
- •54) Операції над множинами.
- •55) Означення функції. Види відображень.
- •56. Складена, обернена функція.
- •57. Параметричне та неявне відображення.
- •58. Аксіоми множин дійсних чисел
- •59. Розширення множини дійсних чисел
- •60. Основні характеристики дійсного числа.
- •61. Обмежені та необмежені числові множини.
- •62. Верхня та нижня межа множини.
- •63 Принцип Архімеда.
- •64. Принцип вкладених відрізків
- •65) Еквівалентність множин та поняття потужності
- •66) Зчисленна потужність
- •67) Континуальна потужність
21. Взаємне розташув 2 площ. Кут між прямою і площиною
 l-напрямний
вектор прямої; N-нормаль(π);
l-напрямний
вектор прямої; N-нормаль(π);
Θ-кут; π/2-θ-кут між векторами.
sinθ=cos(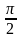 -θ)
=
-θ)
=

В'язка прямих на площині
Якщо задано р-ня 2 прямих на площ, що перетин в т.Р, то можна запис р-ня в'язки прямих, а саме множини всіх прямих, що прох через задану точку.
Нехай т.Р – рез-тат перетину прямих:
(L1): A1x+B1y+C1=0
(L2): A2x+B2x+C2=0
Р-ня в'язки прямих:
α(А1х+В1у+С1)+β(A2x+B2y+C2)=0, де α,β – дійсні числа, єR
1)α=β=0 – немає р-ня
2)α=0; βне=0 – дає р-ня L2
3) αне=0; β=0 – дає р-ня L1
Якщо припустити αне=0, то позначимо λ=β/α і одержимо наступне р-ня в’язки
А1х+В1у+С1+λ(А2х+В2у+С2)=0
В'язка площин в просторі
Множина всіх площин, що прох через пряму, задану загал р-ням:
Нехай пряма L в просторі задана як рез-т перетину 2 площин:
(π1): А1х+В1у+С1z+D1=0
(π2): A1x+B1y+C2z+D2=0
Р-ня в’язки площин:
α(А1х+В1у+С1z+D1)+β(A2x+B2y+C2z+D2)=0
Якщо λ=β/α можна записати
А1х+В1у+С1z+D1+λ(A2x+B2y+C2z+D2)=0
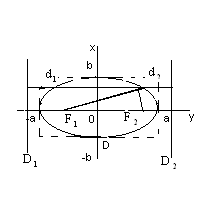
22. Канонічне рівняння еліпса, його геометричні властивості.
1) Еліпсом називається множина точок площини, для яких сума відстаней до 2-ох фіксованих точок(фокусів) є величиною сталих.
Складемо рівняння еліпса
Нехай F1,F2 –фокус еліпса. Якщо F1=F2 то еліпс являється колом.
Вибираємо систему координат так, щоб фокуси мали координати
F1(-c;0)
F2(c;0)
c
> 0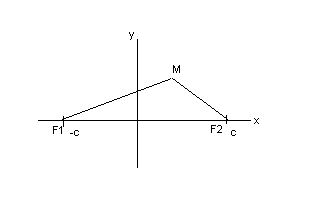 |F1
F2|
= 2c
Беремо довільну точку М(х;у)
|F1
F2|
= 2c
Беремо довільну точку М(х;у)
|M
F1|
= r |M
F2|
= r
;
r
, r
- фокальні радіуси точки еліп: r
+
r
=2a,
a>0
a>c(з
властивостей сторін трикутника)
|M
F2|
= r
;
r
, r
- фокальні радіуси точки еліп: r
+
r
=2a,
a>0
a>c(з
властивостей сторін трикутника)
r
= |M
F1|
=
 r
r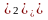 = |M
F2|
=
= |M
F2|
=
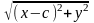
підставляємо в рівняння зв’язку і будемо мати
+
=2а;(x
+ c)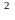 +
y
=4a
-
4a
+
(x-c)
+
y
a
=a
-
cx
+
y
=4a
-
4a
+
(x-c)
+
y
a
=a
-
cx
a
x
-
2a
cx
+a
c
+
a
y
=
a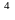 -
2a
cx
+ c
x
(a
-
c
)x
+
a
y
= a
(a
-
c
)
-
2a
cx
+ c
x
(a
-
c
)x
+
a
y
= a
(a
-
c
)
b=
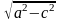 b
=
a
-
c
b
=
a
-
c
b x + a y = a b інакше
|
Властивості еліпса:
1)|x| ≤ a ; |y| ≤ b еліпс знаходиться в серед прямок із сторонами 2а і 2b еліпс має 2 осі симетрії , та центр симетрій. якщо еліпс задано р-м 1, то ОХ, ОУ –вісі симетрії 0-центр симетрії.Вісі симетрії назив гол осями еліпса, центр симетрії-центром еліпса.точки перет еліпса з головними осями називаються ВЕРШИНАМИ еліпса
2) Еліпс є результатом стиснення кола.
23. Гіпербола – множина точок площини, різниця відстаней яких до двох заданих точок (фокусів) є величиною сталою.
F1(-c;0) F2(c;0) c>0 |r1-r2|=const=2a c>a r1=√((x+c)2 +y2); r2=√((x-c)2+y2
|√((x+c)2 +y2 ) - √((x-c)2 +y2 )| =2a
x2/a2 - y2/(c2-a2) = 1 ;c2 - a2=b2 ;
x2/a2 - y2/b2=1 – канонічне р-ня гіперболи а,b –довж півосей гіперболи
Властивості:
x2/a2>=1 точки гіп. розташ в обл |x|>=a. В смузі|x|<a точок Г нема
Г. Має 2 вісі симетрії Ох і Оу, центр симетрії – точка О
Г. має 2 вершини А1(-а;0) А2(а;0)
Точок перетину з віссю Оу не має. Оу – уявна вісь, Ох – дійсна вісь.
можна довести, що Г. Має 2 асимптоти у=(b/a)x і у= - (b/a)x
одноч з розглянутою гіперболою вводять спряжену гіперболу, яка задається рівнянням x2/a2 - y2/b2= -1 В1=(0;-b) В2=(0;b)
Ексцентриситет гіперболи – Е=с/а>1
Директриси: х=а/Е і х= - а/Е
Властивість директриси Г: r1/d1=r2/d2=E
Фокальні радіуси для правої частини Г: r1=Ex+a r2=Ex – a лівої: r1= - Ex + a r2= - Ex – a.
24. Парабола – множина точок площини рівновіддалених від заданої точки (фокуса) та заданої прямої (директриси).
Позначимо відстань від фокуса до директриси р.
F(p/2;0)
D: x=-p/2
M(x;y) – поточна точка
d=r ( d=відстань від точки М до директр, r=відстань від М до фокуса)
p/2+x=√((x-p/2)2 +y2)
(p/2+x)2=(x-p/2)2+y2
y2=2px –канонічне р-ня параболи, де р-параметр (р=відстань від фокуса до директриси)
Властивості
1. Параб має вісь симетр Ох та верш. Пар лежить правіше осі Оу.
E=r/d=1
Якщо парабола симетрична відносно Оу, то її рівняння x2=2py
25.Крив 2 порядку назив. множ точок площ, що задовольняють р-ня
 З’ясуємо,
що являє собою крива 2-го порядку
геометрично. Для цього спочатку повернемо
систему координат
З’ясуємо,
що являє собою крива 2-го порядку
геометрично. Для цього спочатку повернемо
систему координат
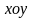 на кут
проти годинникової стрілки так, щоб у
рівнянні зник добуток
на кут
проти годинникової стрілки так, щоб у
рівнянні зник добуток
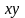 .
.
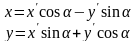

Випишемо
коефіцієнти при
 в
рівнянні кривої
в
рівнянні кривої

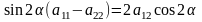
Якщо
 Якщо
Якщо


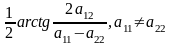

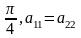
Вважаємо, що поворот с-ми коорд відбувся, тоді р-ня кривої:
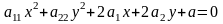 Розглянемо
такі випадки:
Розглянемо
такі випадки:
1 .
.
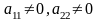 Зробимо заміну змінних
Зробимо заміну змінних
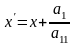
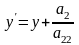
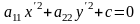
а)
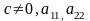 одного знаку протилежного С, тоді ця
крива еліпс.
одного знаку протилежного С, тоді ця
крива еліпс.
б)
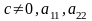 протилежних знаків, тоді на виході крива
гіпербола.
протилежних знаків, тоді на виході крива
гіпербола.
в)
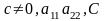 одного знаку уявна
крива
одного знаку уявна
крива
г)
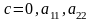 різних знаків – дві прямі, що перетинаються
різних знаків – дві прямі, що перетинаються
д)
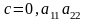 одного знаку – дійсна точка
одного знаку – дійсна точка
2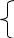 .
Нехай
.
Нехай
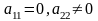

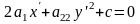
а)
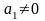 - парабола б)
- парабола б)
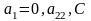 - різн знаків, пара парал пр в)
- одн знаку, пара уяв пр г)
- різн знаків, пара парал пр в)
- одн знаку, пара уяв пр г)
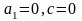 - пара пр, що збіг
- пара пр, що збіг
26.Матрицею
А розмірів
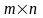 назив. сукуп чисел (елем матриці) розміщ
у вигляді прямокутної таблиці, яка має
m-рядків
і n-стовпців
назив. сукуп чисел (елем матриці) розміщ
у вигляді прямокутної таблиці, яка має
m-рядків
і n-стовпців

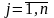
Мат А і В назив. рівними,якщо вони мають одн розм і їх відп елем рівні
Види матриць
1) Матриця, всі елементи якої рівні нулю назив. нульовою (θ)
2) матриця назив. квадр порядку n, якщо m=n. (інша-прямокутна)
3) М, що скл з одного стовпця (рядка) назив. матрицею-стовп (-ряд). Ці матриці також назив векторами.
4)
М
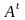 розм
назив. транспон до М А, розмірів
,
якщо
одерж з А перетвор стовпців у рядки з
тим самим номером
розм
назив. транспон до М А, розмірів
,
якщо
одерж з А перетвор стовпців у рядки з
тим самим номером
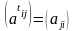
5)
М А назив. симетрич (кососиметричною),
якщо
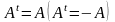
6)
Діагонал елем М А назив. його ел
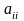 ,
решта ел назив. позадіаг. Квадратна М А
назив. діаг, якщо всі її позадіаг ел
дорівнюють нулю.
,
решта ел назив. позадіаг. Квадратна М А
назив. діаг, якщо всі її позадіаг ел
дорівнюють нулю.
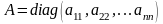
Якщо всі діагональні ел рівні між собою, то така матр назив. скалярною. Якщо у такої матриці всі діаг ел дорівнюють 1, вона назив. одиничною.
(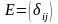 )
)
7) Якщо всі ел матриці розміщ нижче(вище)гол діаг = 0, то така М назив. верхньою(нижньою) трикут.
8)
Квадратна М А назив. невиродж (виродж),
якщо
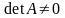 (det
A=0)
(det
A=0)
Лінійні операції
Сумою
матриць А і В однак розмірів назив. матр
А+В тих же розм ел якої дорівн сумам
відпов ел матриць А і В.
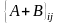 - ij-ий
ел М А+В
- ij-ий
ел М А+В
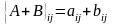
Добутком
матриці А на число
назив. М
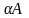 тих самих розмірів, що і А, ел якої є
добутк відпов ел А на число
тих самих розмірів, що і А, ел якої є
добутк відпов ел А на число
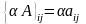
Властивості лінійних операцій над матрицями
1) 1 А=А 1=А
2) 0 А=А 0 = 0(нуль-матриця)
3)

4) А+В=В+А (комутативність)
5)
А+(В+С)=(А+В)+С 6)
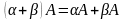 (дистрибутивність)
(дистрибутивність)
7)
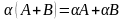 8) А+О=А 9)
8) А+О=А 9)
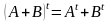
10)
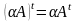

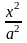 +
+
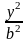 =1
=1