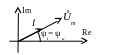Векторные диаграммы элементов
Элементы |
Векторные диаграммы |
Изображения параметров на комплексной плоскости |
|
|
|
|
|
|
|
Ům |
|
|
|
|
Если отобразить систему уравнений линейной цепи с синусоидальными напряжениями и токами в область " "и представить ее относительно комплексных амплитуд, то она по структуре будет подобна уравнениям линейной резистивной цепи, но с комплексными числами, отображающими токи, напряжения и параметры . Следовательно, для отображения модели имеем:
- уравнения элементов
;
- уравнения соединений
Из формальной аналогии математических моделей (уравнений цепи) следует применимость всех методов расчета, теорем и эквивалентных преобразований, полученных для линейных резистивных цепей.
Важной характеристикой цепи синусоидального тока является мощность, передаваемая от источника к потребителю синусоидальным током (рис.3.4,а).
Рис.3.4. Источник с потребителем (а), эквивалентная схема (б) и зависимости напряжения, тока, мощности от времени (в)
Если заменить потребитель эквивалентным
комплексным сопротивлением
,
а источник – эквивалентным последовательным
соединением идеального источника
напряжения с комплексной амплитудой
и внутреннего комплексного сопротивления
(рис.3.4,б), то можно вычислить
комплексную амплитуду
напряжения на входе потребителя (выходе
источника) и представить его функцией
.
Передаваемая мгновенная мощность
,
( рис.3.4,в ), определяется выражением:
,
(3.10)
где
- угол сдвига начальной фазы тока
относительно начальной фазы напряжения
на потребителе. Первая составляющая в
(3.10) есть среднее значение, т. е. постоянная
составляющая и представляет собой
активную мощность Р, которая
рассеивается в потребителе.
.
(3.11)
Для периодических токов и напряжений вводят понятие действующего (среднеквадратичного ) значения:
;
.
(3.12)
Для синусоидальных функций действующие значения имеют однозначную связь с амплитудными и не зависят от начальных фаз:
;
.
(3.13)
Величина
называется коэффициентом мощности,
который является очень важным показателем
в энергетических оценках.
Вторая составляющая в (3.10) изменяется с удвоенной частотой и отражает пульсирующую мощность.
Соотношение составляющих определяется
характером комплексного сопротивления
потребителя
,
т. е. характером нагрузки (индуктивная
или емкостная) и зависит от фазового
сдвига φ. При
(резистивная нагрузка) потребляемая
мощность максимальная
.
При
(индуктивная нагрузка) и при
(емкостная нагрузка) активная мощность
не потребляется, т. е.
и
.
Но существует пульсирующая мощность,
которая в течение части периода идет в
потребитель, а в остальную часть периода
возвращается в источник (см. рис.3.4,в
и выражение 3.10). Активная мощность
рассеивается на резистивных элементах
в виде тепла. Ее выражение можно
представить в виде
.
(3.14)
Действующее значение периодического тока выделяет на резисторе мощность, как и равное ему значение постоянного тока.
3.1.В. КОМПЛЕКСНАЯ МОЩНОСТЬ
При расчете цепей с использованием комплексных амплитуд вводят понятие комплексной мощности
,
(3.15)
где
- действующие комплексное значение
напряжения и комплексно-сопряженное
значение тока. Комплексная величина
может быть представлена тремя формами.
Показательная:
,
(3.16)
где
– модуль комплексной мощности, называемый
полной мощностью,
а
– аргумент комплексной мощности,
определяемый, как
.
Очевидно, что полная мощность представляет
собой максимально возможное значение
активной мощности электрического
аппарата, а аргумент равен, в общем
случае, аргументу полного комплексного
сопротивления цепи
,
(см. рис.3.4,б).
Алгебраическая:
, (3.17)
где
– действительная часть комплексной
мощности или активная
мощность,
– мнимая часть комплексной мощности
или реактивная
мощность.
Размерности комплексной мощности:
(вольт-амперы);
(ватты);
(вольт-амперы реактивные).
Тригонометрическая форма представления:
является вспомогательной при вычислениях.
Комплексная мощность
есть комплексное число, которому
соответствует точка на комплексной
плоскости в первом или в четвертом
квадрантах с координатами
.
Эти координаты и отрезок, изображающий
модуль
,
образуют треугольник
мощностей (рис.3.5).
Рис.3.5.
Треугольники мощностей
и
на комплексной плоскости
Составляющие комплексной мощности, передаваемые от источника в потребитель, вычисляются с использованием эквивалентных схем (см. рис.3.4) по формуле
.
(3.18)
При заданных параметрах активного
двухполюсника (источника)
несложно записать выражение активной
мощности
и с использованием соотношений
и
получить условия передачи максимума
мощности в потребитель
и
.
Максимальная активная мощность
выделится в потребителе при согласовании
сопротивлений:
,
где
- сопряженное значение сопротивлению
.