Имитационное моделирование Игра «Жизнь»

Имитационное моделирование широко применяется в биологии. Рассмотрим одну из самых распространенных имитационных моделей, предложенную Джоном Конвеем - игра «Жизнь».

Для построения алгоритма игры рассмотрим квадратное поле из n+1 столбцов и строк с обычной нумерацией от 0 до n. Крайние граничные столбцы и строки для удобства определим как «мертвую зону», они играют лишь вспомогательную роль.

Для любой внутренней клетки поля с координатами (i,j) можно определить 8 соседей. Примем, что если клетка живая, то ее закрашиваем, если клетка мертвая, то она пустая.

Зададим правила игры.

Если клетка (i,j) живая и в окружении более трех живых клеток, то она погибает (от перенаселения). Живая клетка также погибает, если в окружении менее двух живых клеток (от одиночества). Мертвая клетка оживает, если вокруг нее имеется три живые клетки.

Начальное количество живых клеток и расположение их на поле определяется либо случайным образом, либо мы можем задать нужное нам количество живых клеток и определить их расположение определенным образом и смотреть, как они будут себя вести. Есть устойчивые структуры - пропеллер - три клетки в ряд, есть стабильные структуры - квадрат с просветом внутри, есть структуры, которые повторяют себя через определенное количество циклов и т.д.

Если располагать клетки случайным образом, то с помощью игры жизнь можно построить модель внутривидовой конкуренции (трава - зайцы), межвидовой конкуренции (зайцы - лисы), модель распространения инфекции и т.д.

Уравнения матфизики

Для более сложных физических явлений, таких как процессы колебания, волновые процессы, процессы теплопроводности не всегда удается построить такие простенькие модельки. Реально эти процессы описываются дифференциальными уравнениями 2 порядка, уравнениями в частных производных, называемых уравнениями матфизики.

Напомню, что дифференциальным уравнением называется уравнение, куда входит искомая функция со своими производными

F(x,y(x),y'(x),y''(x):y⁽ⁿ⁾(x))=0

Моделирование процесса теплопроводности

В качестве примера модели, в основе которой лежит уравнение матфизики, рассмотрим модель распространения тепла в однородном стрежне. Задача теплопроводности.

Процесс теплопроводности возникает, если тело неоднородно нагрето. Простейшая для изучения теплопроводности система - линейный однородный стержень. В простой модели боковая поверхность стержня считается теплоизолированной, т.е. через нее нет обмена теплом с окружающей средой.

Обозначим температуру стержня в точке с координатой х в момент времени t через u(x,t). Уравнение теплопроводности имеет вид

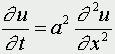
где а - коэффициент температуропроводности, зависящий в первую очередь от вещества, из которого сделан стержень.

Уравнение теплопроводности сопровождается начальными и краевыми условиями, делающими постановку задачи физически однозначной Напомню, что если для дифуравнения заданы начальные условия (условия в начальный момент времени), то такая задача называется задачей Коши, если же заданы краевые условия (на границах исследуемой области), то такая задача называется краевой задачей, если заданы и начальные и граничные условия, то мы имеем смешанную краевую задачу. Начальное условие задает распределение температуры в стержне в начальный момент времени (считаем его равным нулю):

u(x,0) = φ(x)

Краевые условия (их должно быть в данном случае два) указывают, в простейшем варианте, какая температура поддерживается на концах стержня:

u(0,t)=ψ₀(t), u(l,t)=ψ_l(t)

Заметим, что начальные и граничные условия должны быть согласованы, т.е.

u(0,0) = φ(0)=ψ₀(0)

u(l,0) = φ(l)=ψ_l(0)

Моделирование процесса теплопроводности связано с дискретизацией, как временного изменения температуры, так и пространственного.

Введем равномерную прямоугольную сетку с помощью координатных линий

x_i=ih, i=0,1,....n,

t_j=jτ, j=0,1,....m,

где h - это шаг по пространству, по координате х, а τ - шаг по времени.

Значения функции в узлах сетки обозначим u_i^j=u(x_i,t_j).

Входящие в уравнение производные заменим их конечно-разностными аппроксимациями

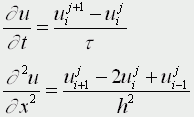
получим

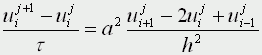
Построенная схема позволяет нам находить значение функции температур на j+1 слое через значения на j слое. Для начало счета при j=0 необходимо знать значения функции температур на нулевом слое. Они нам известны из начальных условий.