1.6. Особенности имитационного моделирования и его преимущества

В определенные моменты функционирования большинства систем возникает необходимость их исследования с целью получения представления о внутренних соотношениях между их компонентами и вычисления их производительности в новых условиях эксплуатации. На рис. 1.5 изображены различные альтернативные способы исследования системы. Рассмотрим их подробнее.

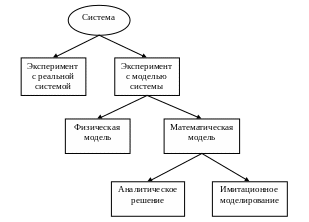
Рис. 1.5. Способы исследования системы […]

Эксперименты с реальной системой или моделью системы? При наличии возможности физически изменить систему (если это рентабельно) и запустить ее в действие в новых условиях лучше всего поступить именно так, поскольку в этом случае вопрос об адекватности полученного результата исчезает сам собой. Однако часто такой подход неосуществим из-за больших затрат на его осуществление, либо в силу разрушительного воздействия на саму систему. Например, в банке ищут способы снижения расходов, и с этой целью предлагается уменьшить число кассиров. Если попробовать в действии новую систему – с меньшим числом кассиров, это может привести к длительным задержкам в обслуживании посетителей и отказу от услуг банка. Более того, система может и не существовать на самом деле, но мы хотим изучить различные ее конфигурации, чтобы выбрать наиболее эффективный способ выполнения. Примерами таких систем могут служить транспортные сети, склады, терминалы и прочие логистические системы. Поэтому необходимо создать модель, представляющую систему, и исследовать ее как заменитель реальной системы. При использовании модели всегда возникает вопрос – действительно ли она в такой степени точно отражает саму систему, чтобы можно было принять решение, основываясь на результатах моделирования.

Физическая модель или математическая модель? В некоторых случаях создание физических моделей может оказаться весьма эффективным инструментом исследования технических систем или систем управления. Примерами могут служить масштабные настольные системы погрузочно-разгрузочных систем и грузовых терминалов. Однако преобладающее большинство создаваемых моделей являются математическими. Они представляют систему посредством логических и количественных отношений, которые затем подвергаются обработке и изменениям, чтобы определить, как система реагирует на изменения, точнее – как бы она реагировала, если бы существовала на самом деле.

Аналитическое решение или имитационное моделирование? Чтобы ответить на вопрос о системе, которую представляет математическая модель, следует установить, как эту модель можно построить. Когда модель достаточно проста, можно вычислить ее соотношения и параметры и получить точное аналитическое решение, то лучше исследовать модель именно таким образом, не прибегая к имитационному моделированию. Однако многие системы чрезвычайно сложны, они практически полностью исключают возможность аналитического решения. В этом случае модель следует изучать с помощью имитационного моделирования, т.е. многократного испытания модели с нужными входными данными, чтобы определить их влияние на выходные критерии оценки работы системы.

Таким образом, имитационное моделирование – это деятельность по разработке программных моделей реальных или гипотетических систем, выполнение этих программ на компьютере и анализ результатов компьютерных экспериментов по исследованию поведения моделей. Имитационное моделирование имеет существенные преимущества перед аналитическим моделированием в тех случаях, когда:

• отношения между переменными в модели нелинейны, и поэтому аналитические модели трудно или невозможно построить;

• модель содержит стохастические компоненты;

• для понимания поведения системы требуется визуализация динамики происходящих в ней процессов;

• модель содержит много параллельно функционирующих взаимодействующих компонентов.

Во многих случаях имитационное моделирование – это единственный способ получить представление о поведении сложной системы и провести ее анализ.