Вопрос №36

<В процессе модерации>

Вопрос №37

<В процессе модерации>

Вопрос №38

Если b = 0, то f(x) – бесконечно малая ФНА

α_n – является бесконечно малой ФНА по определению:

Теорема: бесконечно малая ФНА ограничена.

Доказательство:

α_n – бесконечно малая ФНА, тогда по определению:

Рассмотрим множество K = {1, 2,…,N}. Оно конечное, поэтому max K определён. Тогда можем записать, что | α_n| < [(max K) + 1)] = C. А это и есть определение ограниченной ФНА. α_n – ограниченная ФНА, что и требовалось доказать.

Теорема: Для того, чтобы , необходимо и достаточно, чтобы f(n) – b = β_n, где β_n – бесконечно малая ФНА.

Необходимость: Пусть . Тогда f(n) – b = β_n, где β_n – бесконечно малая ФНА.

Необходимость необходимости: Для того, чтобы необходимо, чтобы f(n) – b = β_n, где β_n – бесконечно малая ФНА.

Достаточность необходимости: Для того, чтобы f(n) – b = β_n, где β_n – бесконечно малая ФНА, достаточно чтобы

Доказательство (необходимость): , тогда по определению:

Значит по определению β_n – бесконечно малая ФНА, что и требовалось доказать.

Вопрос №39

Теорема: Для того, чтобы , необходимо и достаточно, чтобы f(n) – b = β_n, где β_n – бесконечно малая ФНА.

Достаточность: Пусть f(n) – b = β_n, где β_n – бесконечно малая ФНА. Тогда

Необходимость достаточности: Для того, чтобы f(n) – b = β_n, где β_n – бесконечно малая ФНА, необходимо чтобы

Достаточность достаточности: Для того, чтобы достаточно, чтобы f(n) – b = β_n, где β_n – бесконечно малая ФНА.

Доказательство (достаточность): β_n – бесконечно малая ФНА, тогда по определению:

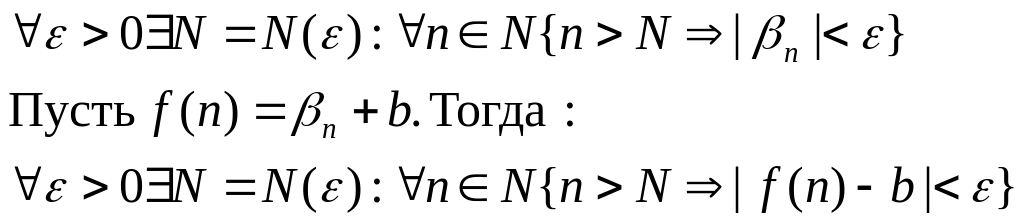
Значит по определению , что и требовалось доказать.

Вопрос №40

Функция f(n) – бесконечно большая ФНА по определению:

Функция f(n) – не бесконечно большая ФНА, когда:

Теорема: Пусть α_n – бесконечно малая ФНА. Тогда А_n = (1/ α_n) – бесконечно большая ФНА

Доказательство: α_n – бесконечно малая ФНА, следовательно:

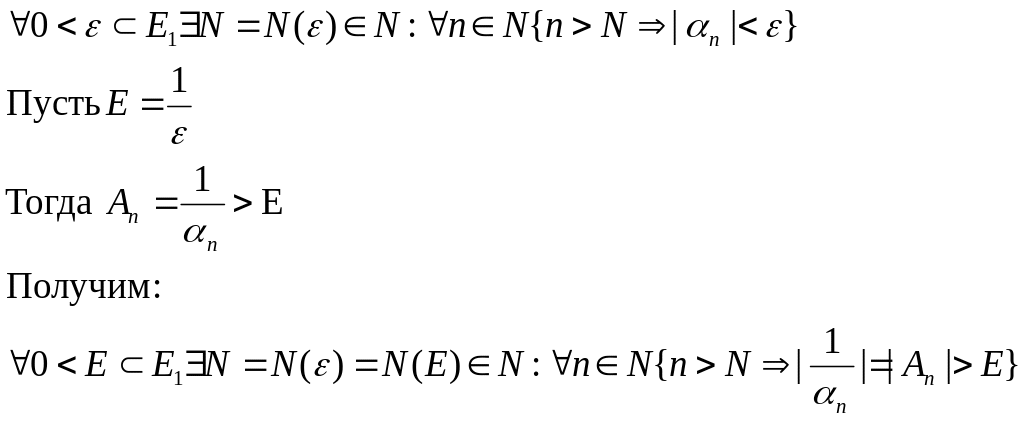
А это есть определение бесконечно большой ФНА. А_n – бесконечно большая ФНА, что требовалось доказать.

Вопрос №41

Теорема: Пусть А_n – бесконечно большая ФНА. Тогда α_n = (1/ А_n) – бесконечно малая ФНА

Доказательство: А_n – бесконечно большая ФНА, следовательно:

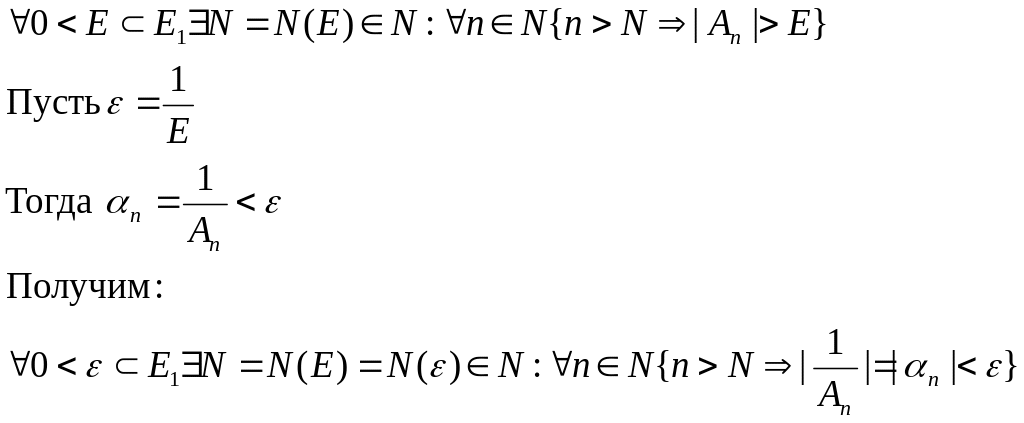
А это есть определение бесконечно малой ФНА. α_n – бесконечно малая ФНА, что требовалось доказать.

20