Вопрос №23

ε-окрестность – это такое множество, каждая точка которого удалена от данной точки х₀ менее, чем на ε.

Пусть , тогда ε-окрестность это множество .

Точка х* называется граничной точкой М ( ) если:

Граница множества М – это множество всех граничных точек М.

Замкнутое множество – это множество, которому принадлежит его граница.

Для двумерного многообразия:

Пусть ε-окрестность – это такое множество

Точка называется граничной точкой М ( ) если:

Вопрос №24

ε-окрестность – это такое множество, каждая точка которого удалена от данной точки х₀ менее, чем на ε.

Пусть , тогда ε-окрестность это множество .

Точка является предельной точкой М, если выполняется или 1), или 2).

1) в содержится бесконечное число точек из М

2) в содержится хотя бы одна точка из М.

Производное множество М’ – это множество всех предельных точек М.

Замкнутое множество – это множество, которому принадлежит его производное множество.

Для двумерного многообразия:

Пусть ε-окрестность – это такое множество

Точка является предельной точкой М, если выполняется или 1) или 2).

1) в содержится бесконечное число точек из М

2) в содержится хотя бы одна точка из М.

Теорема о предельной точке: два определения предельной точки эквивалентны.

Вопрос №25

Докажем эквивалентность двух определений замкнутого множества.

1. Если , то F – замкнутое.

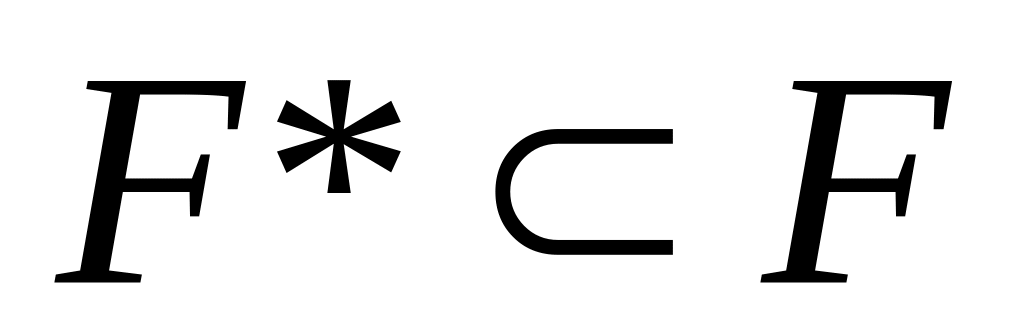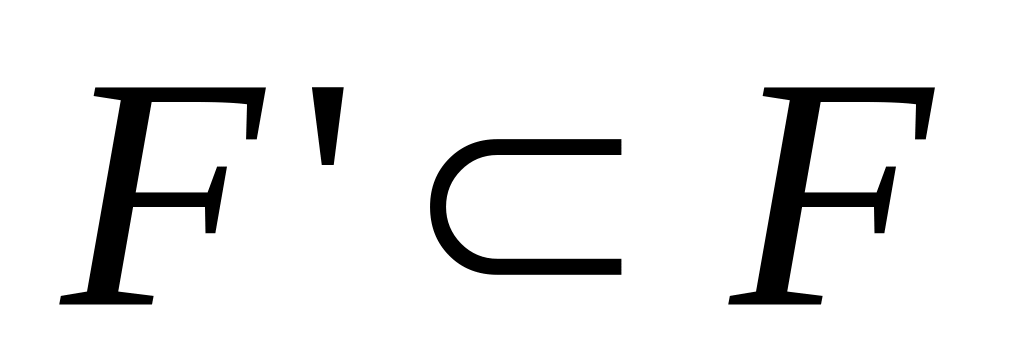2. Если , то F – замкнутое.

Теорема: Для того, чтобы множество F ( ) было замкнутым (т.е.  ), необходимо и достаточно, чтобы  .

Теорема 1 (необходимость): Если М замкнутое (то есть ), то

Доказательство:

А) Если F = E₁, то F’ = F →

Б) Если F’ = ∅ и F ≠ ∅, то

В) Если F’ ≠ ∅ и F ≠ ∅, то каждая предельная точка является или граничной, или внутренней. Если предельная точка является граничной, то она принадлежит F в силу . Если предельная точка внутренняя, то она обязательно принадлежит F. → , что требовалось доказать.

Теорема 2 (достаточность): Если , то F – замкнутое (то есть )

Доказательство:

А) Если F* = ∅, то

Б) Если F* ≠ ∅, то каждая граничная точка является или предельной, или изолированной. Если граничная точка предельная, то она принадлежит F в силу . Если граничная точка изолированная, то она обязательно принадлежит F. → , что требовалось доказать.

Вопрос №26

Точка х’ является предельной точкой М, если в содержится хотя бы одна точка из М.

Для n-мерного многообразия:

Точка х’(х₁’,x₂’,…,x_n’) является предельной точкой М, если в содержится хотя бы одна точка из М.

Вопрос №27

Точка является предельной точкой М, если выполняется или 1), или 2).

1) в содержится бесконечное число точек из М

2) в содержится хотя бы одна точка из М.

Теорема: из 1) следует 2)

Доказательство: если в ε-окрестности точки х’ содержится бесконечное количество точек множества М, то в проколотой ε-окрестности точки х’ содержится на одну точку меньше, то есть бесконечное количество, а значит – и хотя бы одна, что и требовалось доказать.

Вопрос №28

Точка является предельной точкой М, если выполняется или 1), или 2).

1) в содержится бесконечное число точек из М

2) в содержится хотя бы одна точка из М.

Теорема: из 2) следует 1)

Доказательство: Предположим, что если утверждение 2) верно, то утверждение 1) - неверно, то есть в ε-окрестности х содержится конечное число точек.

Пусть . Тогда учитывая конечность выбранного множества мы можем определить . Рассмотрим проколотую ω -окрестность х. Но тогда:

Uω(х) ∩ М = х, откуда следует, что

Но это противоречит условию 2). Наше предположение неверно, утверждение 1) верно, что и требовалось доказать.

Вопрос №29

Теорема: Пусть Е1\G = M, тогда М = F.

Доказательство:

Вопрос №30

Теорема: Пусть Е1\F = М, тогда М = G

Доказательство:

Вопрос №31

Е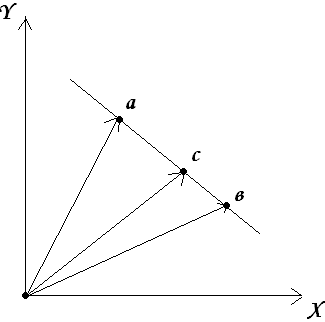 сли 0 ≤ λ ≤ 1, то

– выпуклая комбинация векторов и .

Отрезок - это множество всех выпуклых комбинаций векторов и .

Множество называется выпуклым, если отрезок, соединяющий 2 любые его точки полностью принадлежит данному множеству.

Вопрос №32

Шаром с центром в точке и радиусом r > 0 называется множество

Открытым шаром с центром в точке и радиусом r > 0 называется множество

Шар с центром в точке и радиусом r > 0 также называют окрестностью точки

Сферой с центром в точке и радиусом r > 0 называется множество

Вопрос №33

Открытый шар является открытым множеством, если для любой его точки верно, что

_{Пусть ε = r. Тогда перепишем:}

_{А это и есть определение шара. Значит шар – открытое множество, что и требовалось доказать.}

Вопрос № 34

Т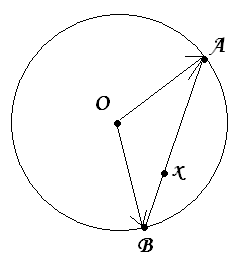 еорема: Двумерный шар с центром в точке и радиусом r > 0 является выпуклым множеством

Доказательство: Заданное множество мы можем изобразить геометрически в виде окружности с хордой:

АВ – отрезок прямой, хорда. По определению хорды АВ лежит в данном круге. Поэтому двумерный шар – выпуклое множество, что и требовалось доказать.

Вопрос №35

Числовая последовательность – это функция, определённая на множестве натуральных чисел и принимающая числовые значения. То есть это функция, аргументом которой является натуральное число. Поэтому числовую последовательность можно определить как функцию натурального аргумента (ФНА)

Пусть дана функция f(n) = n+1

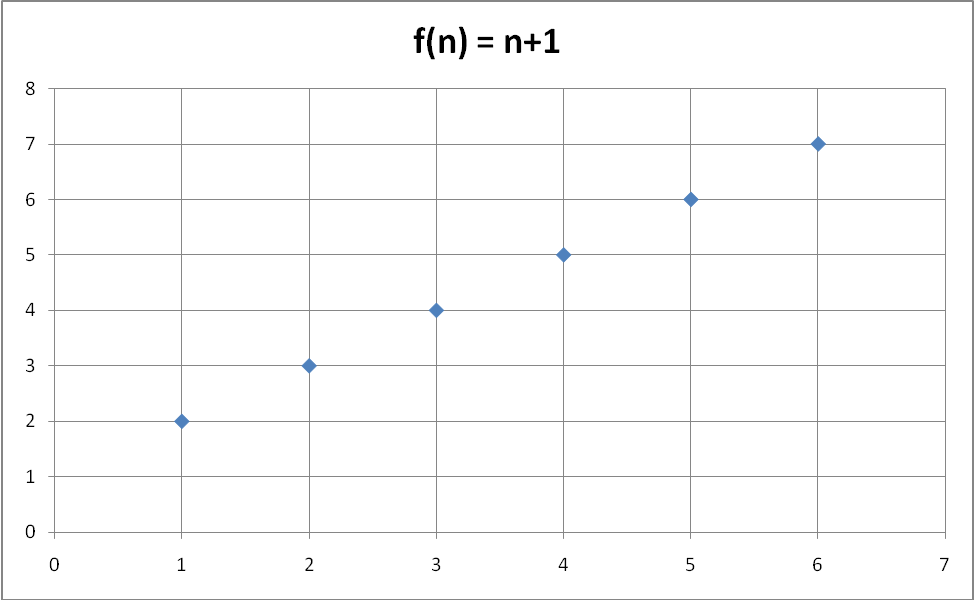
График ФНА – это точки, но не линия.

Рассмотрим вариации графиков ФНА:

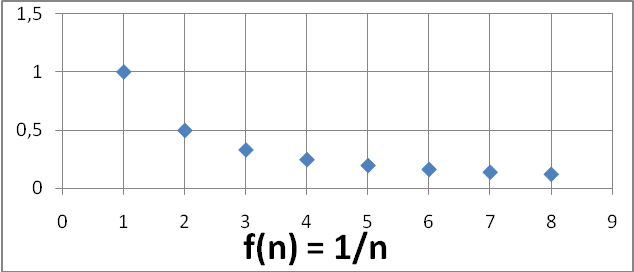
Первый тип – стремится к какому-либо числу:

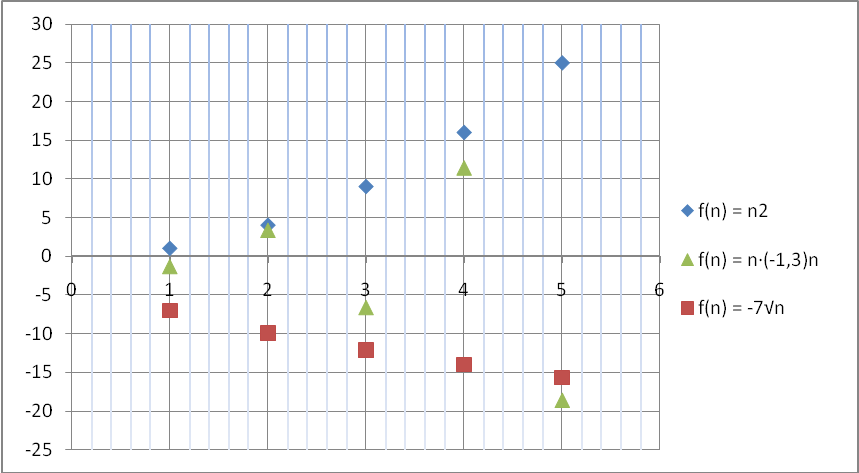
Второй тип – бесконечно возрастает, или бесконечно убывает, или бесконечно возрастает и убывает:

Т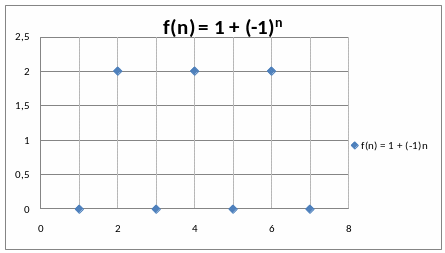 ретий тип – колеблется, ни к чему не приближаясь: