Linear transformations.
Let a
finite-dimensional linear space L
be given. The representation
is called a transformation of the linear space.
The
transformation
is called a linear
transformation
if
.
This means that a linear transformation transform any linear
combination of vectors in a linear combination of the images of these
vectors, moreover, with the same coefficients.
The
following properties of linear transformations are true.
,
.
Let us show some examples:
identity transformation, that is
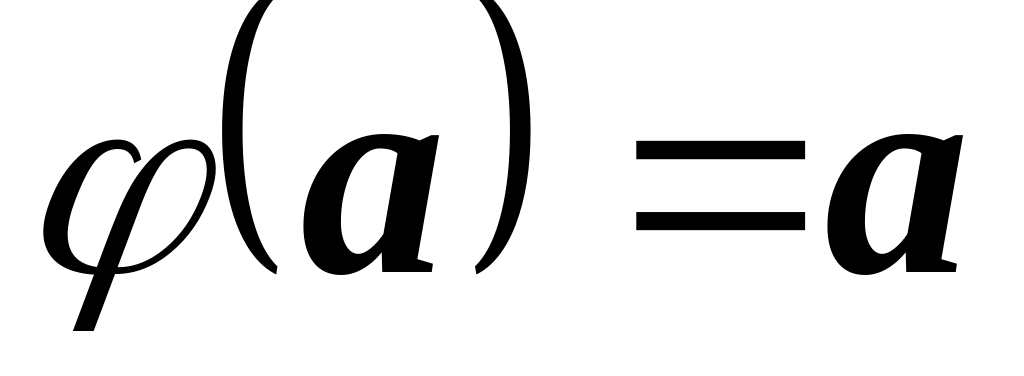;zero transformation, that is
.
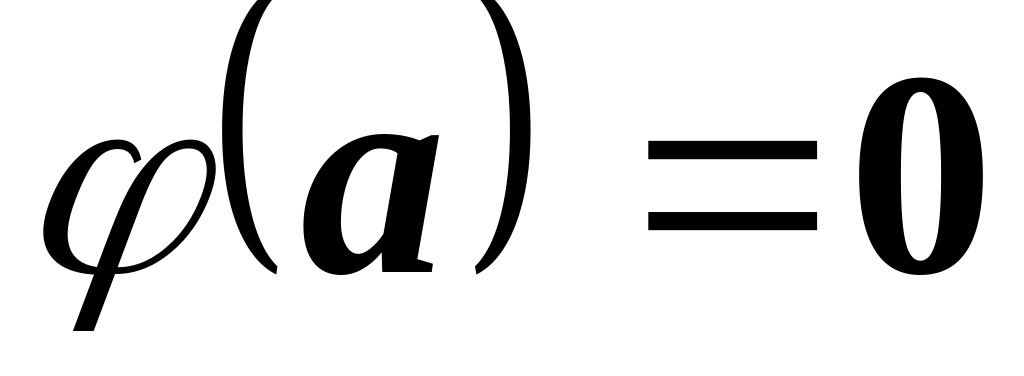Let
be a basis in the linear space L.
Theorem
1.
For an ordered system of vectors
there exists only one transformation
,
such that
.
Thus, we have one-to-one correspondence between all linear transformations and all ordered systems of vectors . However every vector from this system can be represented as a linear combination of the basis vectors :
.
From the
components of the vectors
in the basis
we can form the square matrix
.
Thus, we have one-to-one correspondence between all linear
transformations and all square matrices of the order n,
this correspondence, certainly, depends on the choice of the basis
.
We will say
that the matrix A
defines the linear transformation
or A
is the matrix
of the linear transformation
in the basis
.
If we define
as the images column of the basis, then
and if
,
then
.
The linear transformation is called non-singular
if it is a surjection. The matrix of a non-singular linear
transformation is non-singular (i.e. its determinant is not equal to
zero).
Example
45:
let
be the basis of linear space, matrix A
be the matrix of linear transformation
.
Find the image of the element
,
if
.
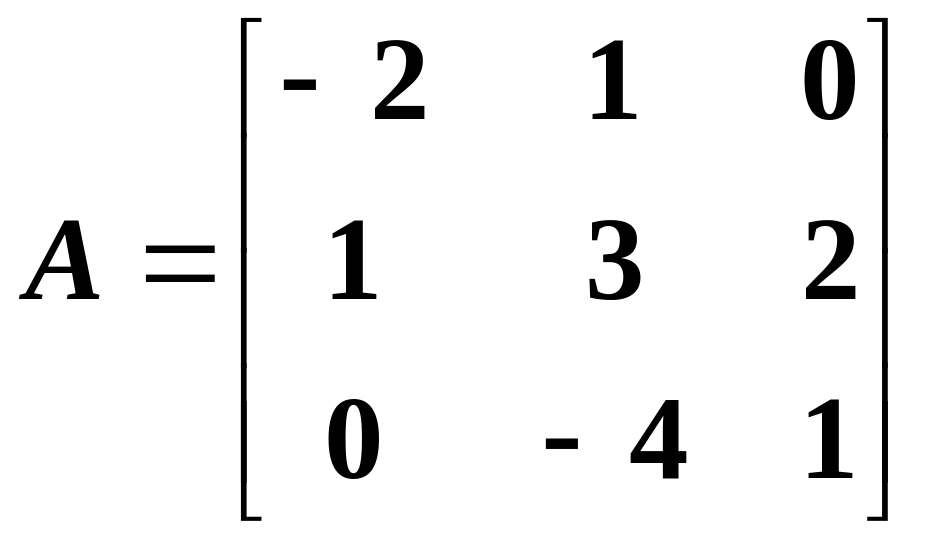Solution:
.
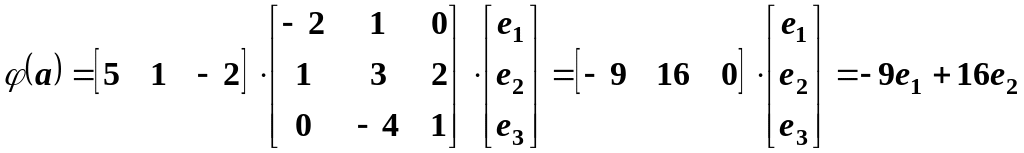Let two
bases
and
,
with the transition matrix T
(
)
be given. And let the linear transformation
in these bases be defined by matrices
and
(
and
.
We have
,
but
,
because
is the linear transformation. Thus,
,
and because e
is the linear independent system
.
Finally, because T
is invertible,
and
.
If two matrices are connected with such a correlation they are called similar. The determinants of similar matrices are equal.