• Homogeneous systems of linear algebraic equations.

The following system of linear algebraic equations is called homogeneous.

From the theorem of Kronecker-Capelli's it follows that this system is always consistent, since adding zero column does not change the rank. Moreover, it is seen that this system has the zero solution.

Let the rank of the coefficient matrix of this system equal r. If then the zero solution will be unique. From the other hand, if the number of equations is less than the number of variables or , then the system always has nonzero solutions.

The solutions of homogeneous systems of linear algebraic equations have the following properties:

1. If is a solution then is also a solution for every k.

2. If and are solutions then is also a solution.

In other words, a linear combination of solutions of the homogeneous system of linear algebraic equations is also a solution of the system.

Theorem 3. If the rank r of the coefficient matrix of the homogeneous system of linear algebraic equations in n variables is less than the number of variables, then there exist linear independent solutions, which are called the fundamental system of solutions.

To find the fundamental system of solutions we take r linear independent equations and solve it for r variables. Then, we take linear independent vectors which are, for instance, columns of the identity matrix of the order . Substituting their components in the found solution for r variables, we obtain the fundamental system of solutions.

Example 40: find the fundamental system of solutions of the following system:

Solution: first of all let us derive the coefficient matrix to the reduced row-echelon form.

Step 1. Interchange the first and the third row:

~ .

Step 2. Add –2 times the first row to the second row, –3 times to the third, –1 times to the fourth:

~ .

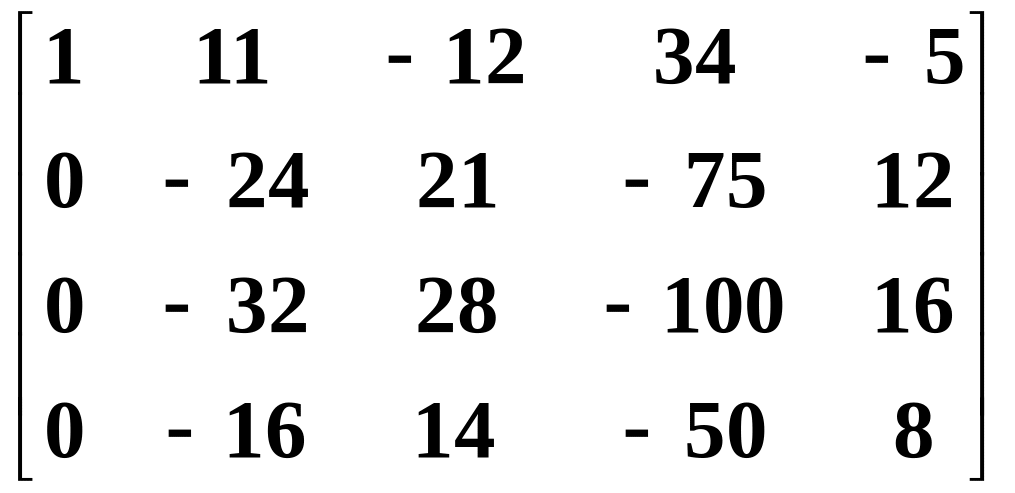Step 3. Divide the second row by –3, the third by 4, the fourth by 2:

~ .

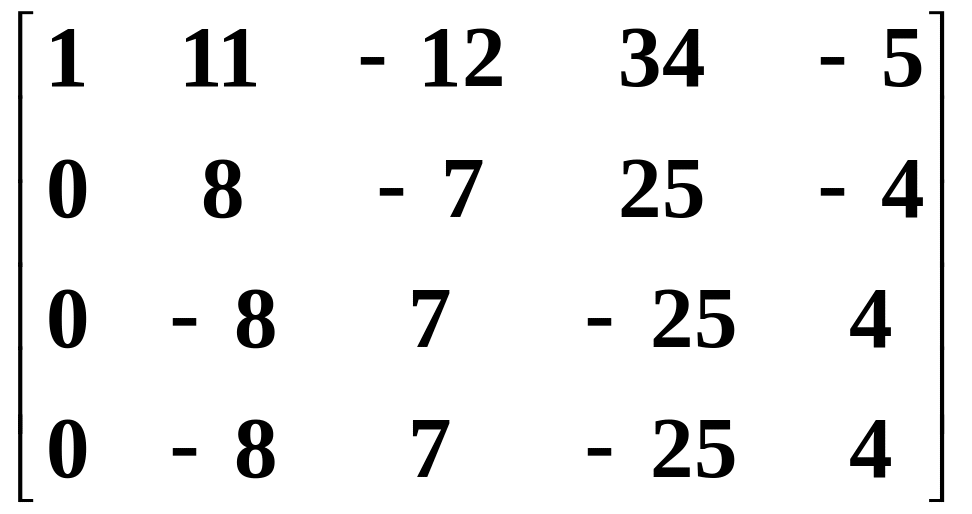Step 4. Add the second row to the third and fourth:

~ .

Step 5. Divide the second row by 8:

~ .

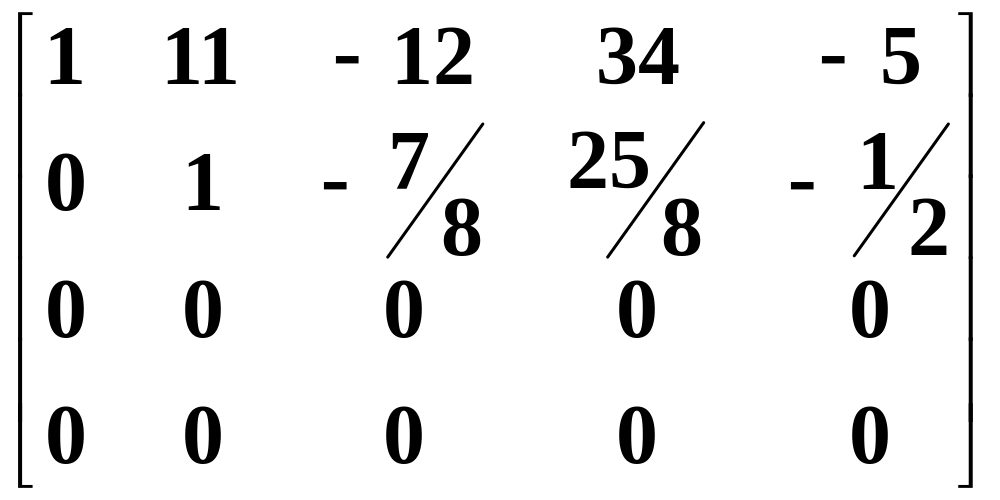Step 6. Add –11 times the second row to the first row:

~ .

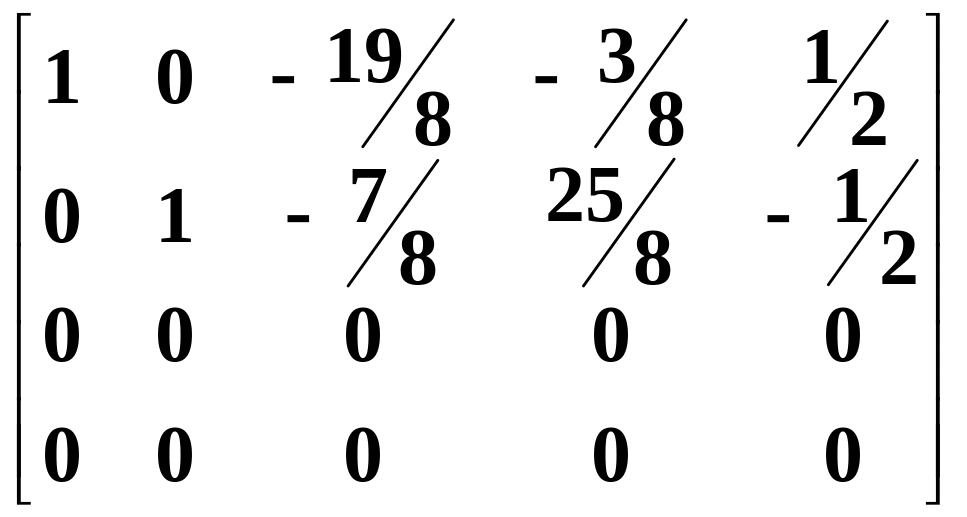We have and Then we take three independent vectors , , and after substituting the components of these vectors for , , we obtain the fundamental system of solutions:

, , .

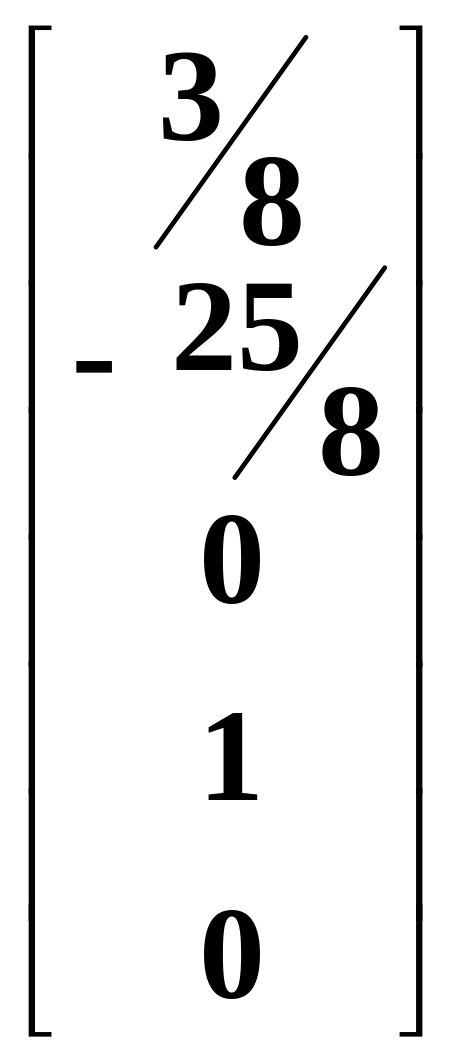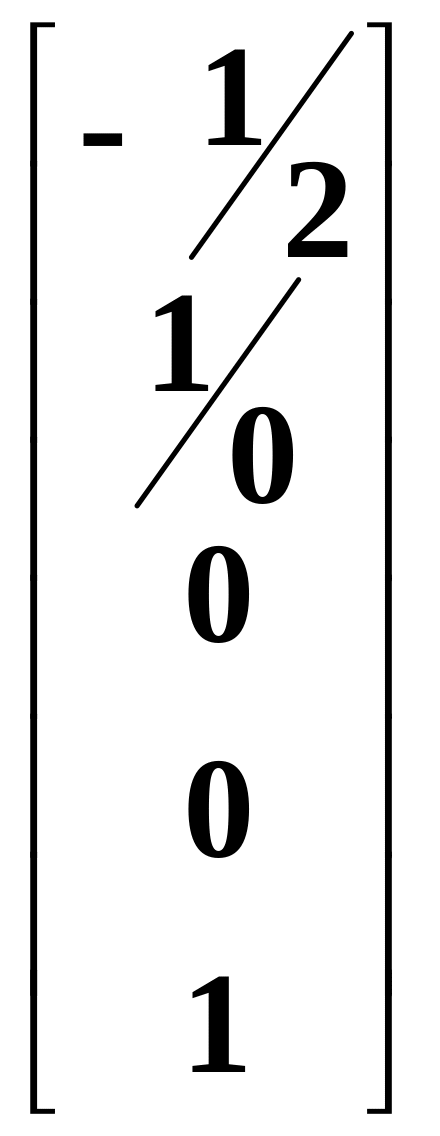• The inverse of a matrix. Matrix equations.

Let A be a square matrix of order n. If there exists a matrix such that , then is the inverse of A. is read "A inverse". Recall that it is not always true that AB=BA, even if both products are defined. However, if A and B are both square matrices and AB=I, then it can be shown that BA=I.

If a matrix a has an inverse, then a is invertible (or non-singular); otherwise, a is singular. A nonsquare matrix cannot have an inverse. Not all square matrices possess an inverse.

Theorem 4. The matrix A is invertible if and only if the determinant of the matrix A is not equal to zero. If the matrix does possess an inverse, then that inverse is unique.

Example 41: show that B is inverse of A, where

, .

Solution:

,

.

There are several methods of finding the inverse of a matrix. Let us consider two of them. The first method is the determinant method. Let A be a square matrix of order n, then

,

where is a minor obtained from A by crossing out i^th row and j^th column, taken with "+" if i+j is even, and with "–" if i+j is odd.

Example 42: find the inverse of the matrix

.

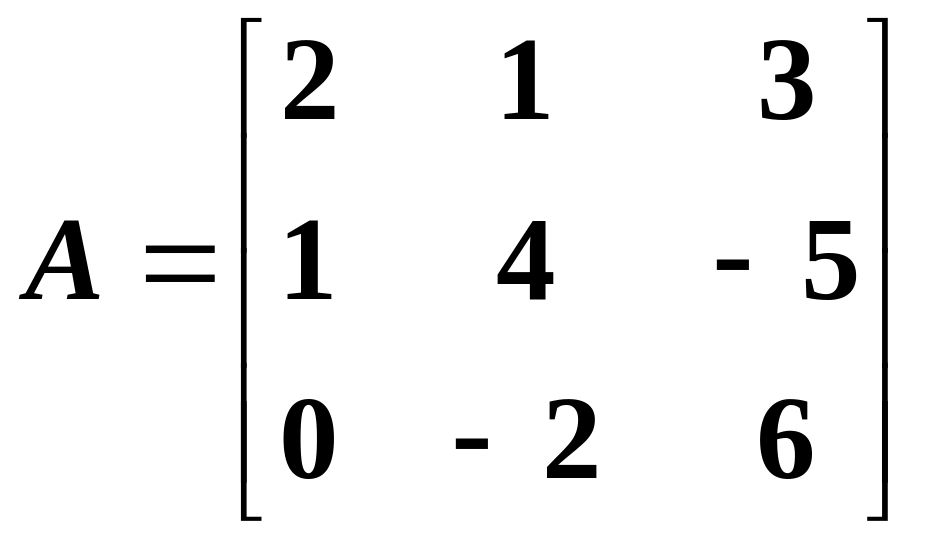Solution: let us find the determinant of A:

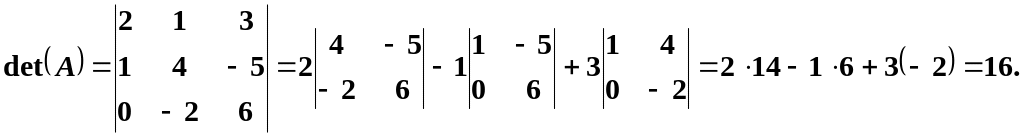
Since, the determinant of A is not equal to zero the inverse matrix exists, and

.

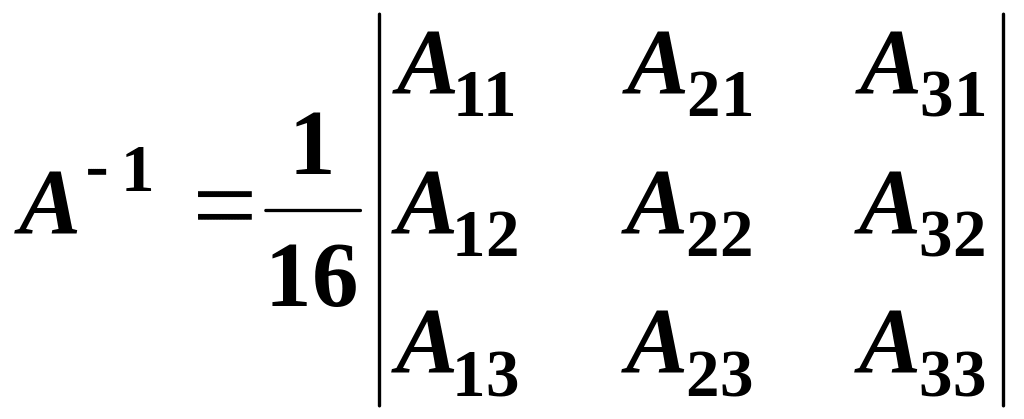Let us find :

, ,

, ,

, ,

, ,

.

Thus, we can write the inverse of A:

.

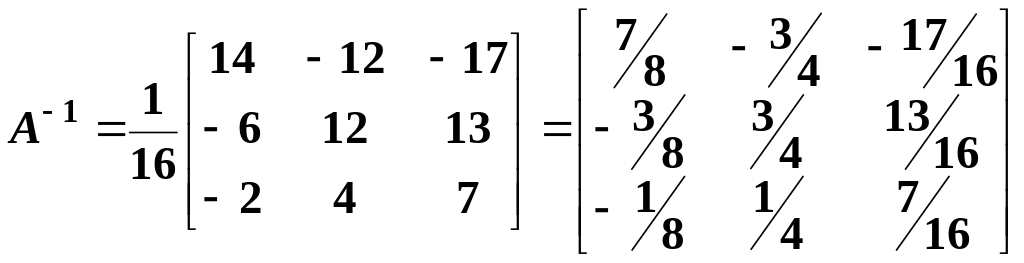The second method is as follows. If we by a sequence of elementary row operations reduce a square matrix to the identity matrix, then with the same sequence of elementary row operations the identity matrix is reduced to the inverse of the given matrix.

The system of n linear algebraic equations in n variables can be rewritten in the following matrix form.

System	Matrix form
	.

Or the system can be rewritten as . If we multiply this equation from the left by , we obtain , then , and finally .

Example 44: solve the following system using the inverse matrix:

Solution: let us rewrite this system as , where

, , .

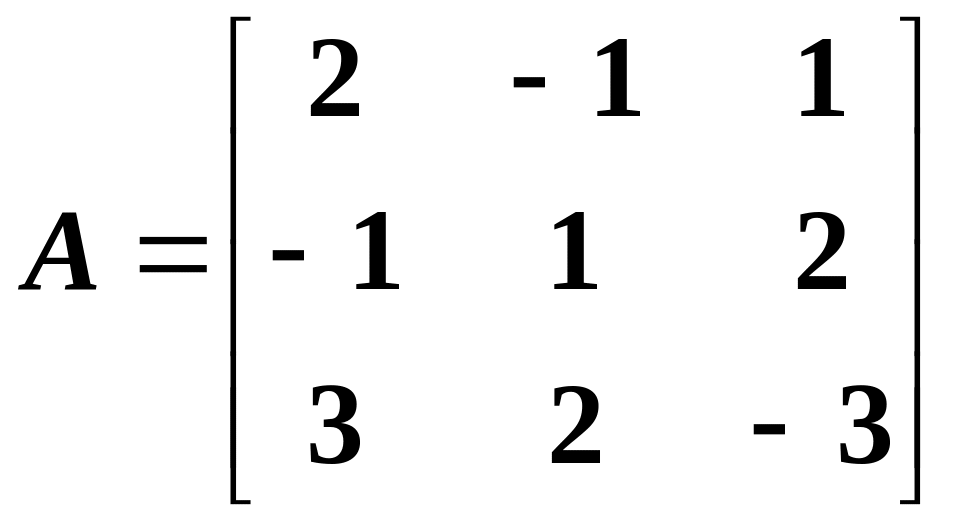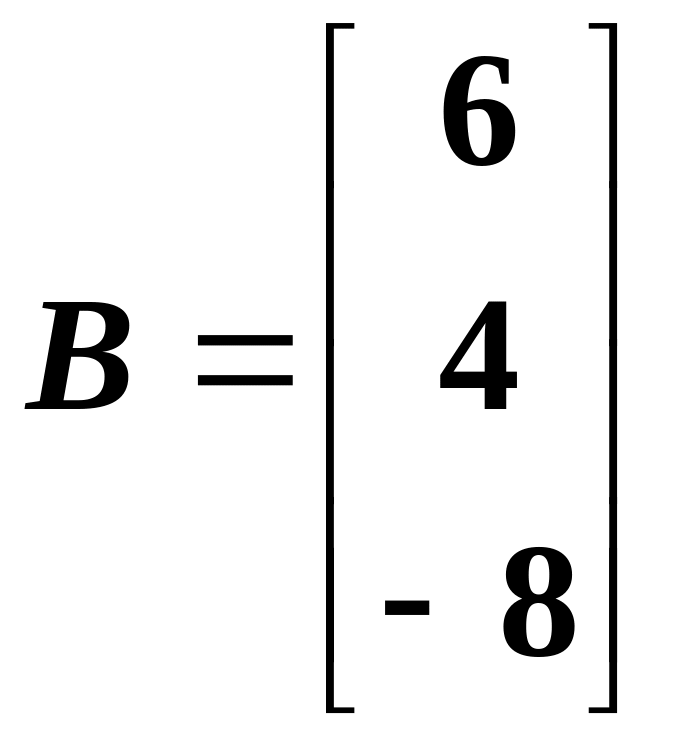Using one of the mentioned methods we obtain

.

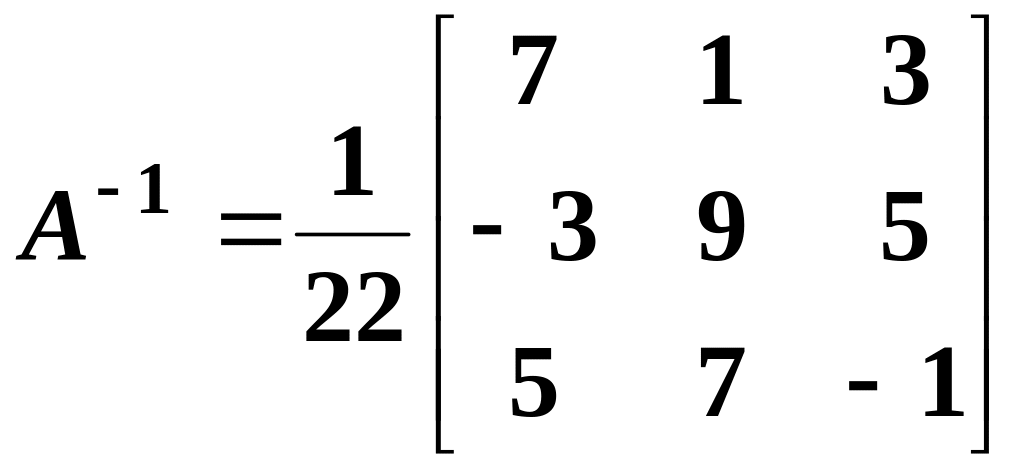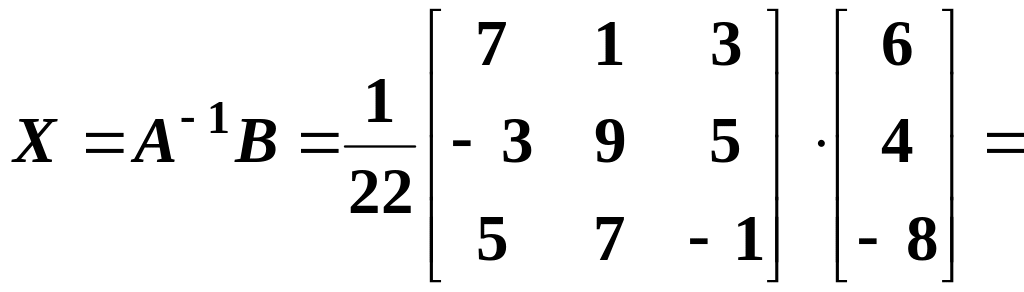
, or

VECTOR spaces
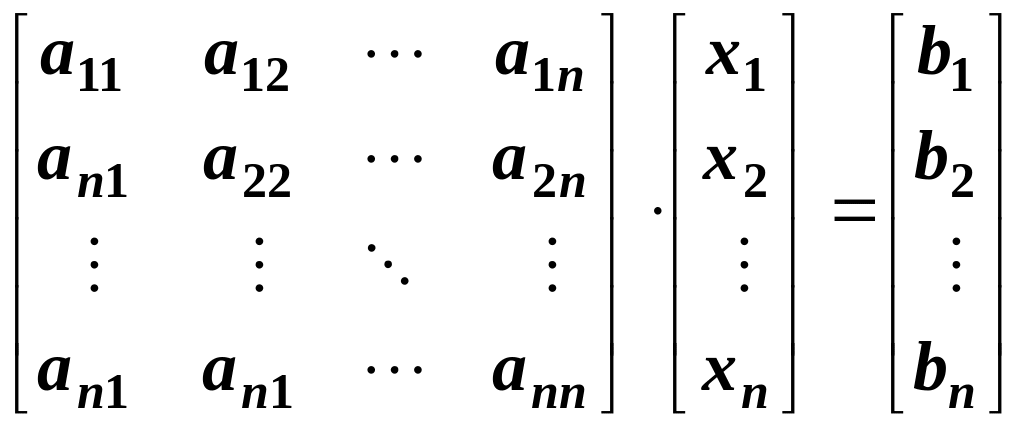