Практическое занятие №3 предел функции

Цель: решения задач по нахождению пределов функции с неопределенностью вида: и .

Контрольные вопросы

1. Сформулируйте понятие числовой последовательности. 2. Какая числовая последовательность называется ограниченной? 3. Какая точка называется предельной для данной числовой последовательности. 4. Сформулируйте теорему Больцано-Вейерштрассе. 5. Сформулируйте понятие предела числовой последовательности. 6. В чем заключается геометрический смысл предела числовой последовательности? 7. Сформулируйте понятие функции. Способы задания функции. 8. Сформулируйте понятие предела функции. 9. Запишите основные свойства пределов. 10. Запишите первый и второй замечательные пределы.

Примеры решения типовых задач

Пример 3.1. Вычислить предел: .

Решение:

.

Пример 3.2. Вычислить предел: .

Решение:

Если вместо подставить 2, то получится неопределенность вида . Чтобы избавится от нее, преобразуем числитель и знаменатель.

Числитель:

Знаменатель:

,

Таким образом:

.

Пример 3.3. Вычислить предел: .

Решение:

Если вместо подставить , то получится неопределенность вида . Чтобы избавится от нее разделим числитель и знаменатель на :

Пример 3.4. Вычислить предел: .

Решение:

Если вместо подставить 0, то получится неопределенность вида .

Преобразуем данный предел:

.

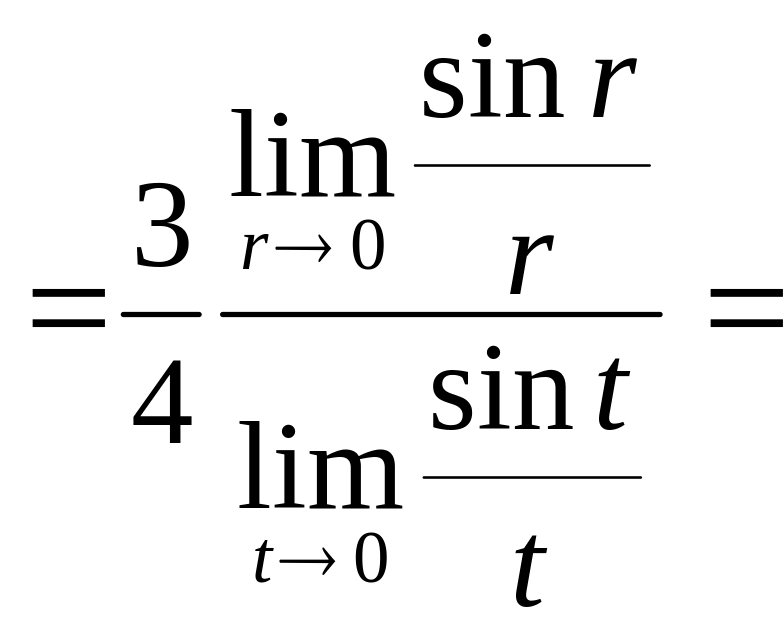
Здесь использовали замену и первый замечательный предел.

Пример 3.5. Вычислить предел: .

Решение:

.

Здесь выполнили замену и второй замечательный предел.

Задачи для самостоятельного решения

3.1. . 3.2. . 3.3. . 3.4. . 3.5. . 3.6. .

Практическое занятие №4 дифференциальное исчисление функции одной переменной

Цель: решение задач по нахождению производной от функции, а также исследовании функции на точки максимумов и минимумов, интервалы возрастания и убывания.

Контрольные вопросы

1. Сформулируйте понятие непрерывной функции в данной точке. 2. Сформулируйте понятие точки разрыва функции. 3. В чем принципиальное различие между точками разрыва первого и второго рода? 4. Сформулируйте понятие производной функции одной переменной. 5. Какая функция называется дифференцируемой в данной точке? 6. В чем состоит геометрический смысл производной? 7. Запишите правило дифференцирования суммы функций. 8. Запишите правило дифференцирования частного функций. 9. Запишите правило нахождения производной от произведения функций. 10. Сформулируйте правило дифференцирования сложных функций. 11. Сформулируйте понятие дифференциала функции одной переменной. 12. Сформулируйте понятие точек максимумов и минимумов функции. 13. Запишите необходимый и достаточный признаки существования точек экстремумов функции.

Примеры решения типовых задач

Пример 4.1. Найти производную функции:

Решение:

.

Пример 4.2. Найти производную функции: .

Решение:

Воспользуемся правилом дифференцирования произведения функций:

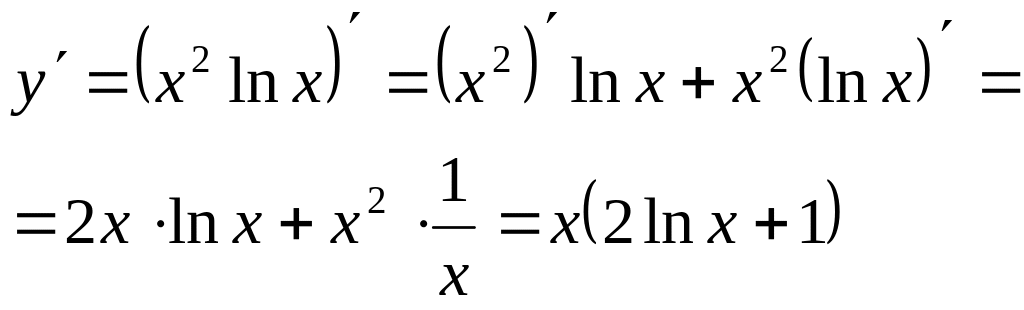
Пример 4.3. Найти производную функции: .

Решение:

Воспользуемся правилом дифференцирования частного .

.

Пример 4.4. Найти производную сложной функции: .

Решение:

Пример 4.5. Исследовать на максимум и минимум функцию: .

Решение:

Находим критические точки. Продифференцируем данную функцию:

.

Находим действительные корни производной:

; .

Производная всюду непрерывна, значит, других критических точек нет.

Исследуем первую критическую точку . Так как , то:

При имеем ;

При имеем .

Значит, при переходе (слева направо) через значение производная меняет знак с плюса на минус. Следовательно, при функция имеет максимум.

Исследуем вторую критическую точку :

При имеем ;

При имеем .

Значит, при переходе (слева направо) через значение производная меняет знак с минуса на плюс. Следовательно, при функция имеет минимум.

.

Пример 4.6. Найти прямоугольный треугольник наибольшей площади, имеющий гипотенузу, равную 10 см.

Решение:

Площадь прямоугольного треугольника можно найти по формуле:

, где и длины катетов. Согласно теореме Пифагора:

, где – длина гипотенузы.

Таким образом, подставив данное выражение в формулу для нахождения площади, получим функцию одной переменной:

.

Нам необходимо найти прямоугольный треугольник наибольшей площади, т.е. по сути, нам необходимо исследовать на экстремумы функцию и найти при каком значении она максимальна.

Находим производную от функции :

Находим критические точки: , , Используя достаточный признак существования экстремума функции, можно определить, что точкой максимума будет . Тогда длина второго катета будет равна: . Таким образом, максимальная площадь будет равна:

см².

Задачи для самостоятельного решения

4.1. Найти производные функций:

а) ; б) ;

в) ; г) .

4.2. Найти производную сложной функции:

а) ; б) ;

в) ; г) .

4.3. Найти экстремумы функции:

а) ; б) .

4.4. Найти наибольшее и наименьшее значения функции на отрезке .

4.5. В тюрьме города Ленинск собрались строить железную камеру для содержания особо опасных преступников. Какое наименьшее количество железа нужно для этой цели, если по санитарным нормам высота камеры должна быть не менее 2,5 м, а ее площадь – не менее 6 м²?