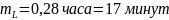1 2 M Входной поток
n
Каналы обслуживания
здесь n – число каналов обслуживания
m –максимальная длина очереди
В ∀ момент времени t заявка из входного потока либо становится в один из каналов на обслуживание, либо в очередь, если все каналы заняты. Под состоянием СМО будем понимать число заявок, находящихся в ней. Оно будет изменяться от 0, когда заявок в системе нет, до n+m, когда все каналы обслуживаются и все места в очереди заняты. Подобную СМО можно представить в виде графа состояний, для которого можно записать описывающие его поведение уравнения. Решив их для ∀ произвольного момента времени (в частности для стационарного режима) можно определить значения вероятностей нахождения СМО в одном из состояний Si
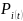i
= 0, n+m t>
0
Зная их можно определить основные характеристики СМО, такие как:
Среднее число занятых каналов обсл-я
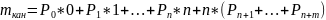
Средняя длина очереди
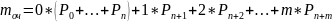
Вероятность, что поступившее в момент времени tтребование получит отказ
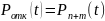
Вероятность, что поступившее требование будет обслужено
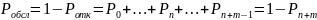
Аналогично может быть найдена:
Вероятность, что требование поступившее в систему сразу поступит в канал на обслуживание
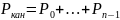
Вероятность, что требование попадёт в очередь
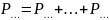
Формула
Литтла
Среди различных математических
выражений, позволяющих определять
основные характеристики СМО в
стационарном режиме особое
место занимает выражение, устанавливающее
связь
между средним
числом заявок ,
находящихся в
системе
(обслуживающих или стоящих в очереди)
и
средним
временем пребывания заявки в системе.
Рассмотрим
СМО – одноканальную, многоканальную,
марковскую, немарковскую, с ограниченной
или неограниченной очередью – и связанные
с нею два потока сообщений: поток
заявок, приходящих в систему
и поток
заявок, покидающих систему.
Если в системе установился
стационарный режим, то среднее
число заявок, прибывающих
в СМО за единицу времени равно
среднему числу заявок, покидающих
её за это же время. Т е оба потока имеют
одинаковую интенсивность.
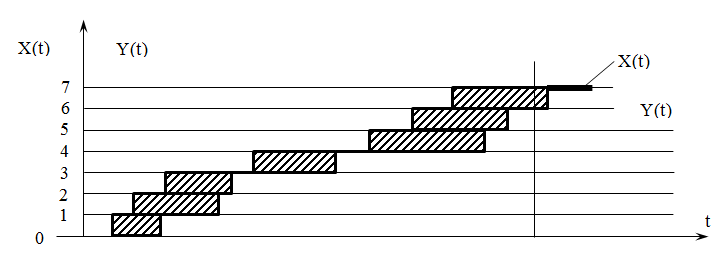
Обозначим: X(t)
– число заявок, прибывающих в СМО, до
момента t,
Y(t)
– число заявок покидающих СМО к моменту
t.
Тогда
Z(t)
= X(t)
– Y(t)
-
- число заявок находящихся в системе
в момент времени t
(см рис)
Найдём
среднее
число заявок, находящихся в системе
для некоторого, достаточно большого
интервала T
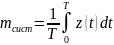
Пренебрегая погрешностью, за счёт отбрасывания части времени обслуживания заявки на конце интервала можно считать, что
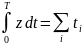
Суммарное время нахождения всех заявок в системе.
Г
де
i–все
заявки, находящиеся в системе за время
T,
ti–время
пребывания i
- й заявки системе.
Подставим значение в выражение для mkдомножив и разделив первую часть полученного выражения наλ
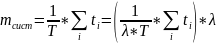
Величинаλ*T – среднее число заявок, поступивших в систему за время T, а
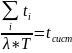
есть среднее время пребывания одной заявки в системе. Отсюда, подставив tсист в выражение для mсист получим
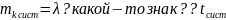
Откуда
следует–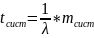
– Формула Литтла.
Формула Литтла : для любой СМО , при любом характере потока заявок , при любом распределении времени обслуживания , при любой дисциплине обслуживания среднее время пребывания заявки в системе равно среднему числу заявок в системе , деленному на интенсивность потока заявок , поступивших в систему или иначе :
=
,
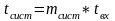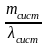
где t
=
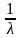- среднее время между двумя соседними
заявками , поступившими в систему.
Аналогично можно получить формулу Литтла для среднего времени пребывания заявки в очереди :
=
.
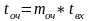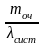Аналогично
=
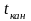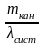, где
-
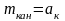среднее число занятых каналов.
Т.к.
среднее время пребывания требования в
канале
равно 1/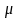
отсюда легко получить выражение для
среднего числа занятых каналов
=
=
.
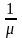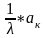
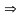
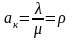Следует
отметить , что во всех случаях
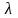характеризует интенсивность требований
, поступивших
в систему ,
в не вообще входной поток заявок.
Если
часть требований из потока заявок на
входе теряется (напр. в системах с
отказами ) , то необходимо скорректировать
значение
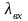приняв вместо него
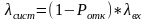, где
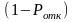- вероятность , что требование поступит
в систему (Не получит отказ).
СМО БЕЗ ОЖИДАНИЯ.
УРАВНЕНИЕ ЭРЛАНГА.
Рассмотрим следующую задачу. Имеется СМО с n каналами обслуживания. На вход системы поступает поток требований(заявок).В случае наличия свободного канала заявка поступает в систему на обслуживание. Если в момент поступления заявки все каналы заняты , то она получает отказ , покидает систему не обслуженной и в дальнейшем обслуживании не участвует . Системы(с отказами) подобного рода называются СМО без ожидания.
Пусть входной поток заявок - простейший с интенсивностью - требований в единицу времени.
Время
обслуживания
заявки T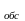
подчинено exp
закону распределения с параметром
.
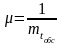В этом случае параметр можно рассматривать как интенсивность потока обслуживания занятого канала (Если он бесперебойно обеспечивается заявками на обслуживание) , являющеюся простейшим потоком.
Составим граф состояний для данной системы.
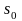
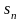
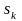
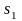
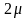
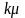
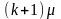
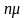
Здесь
состояние
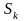(k
=
)
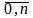соответствует числу заявок , находящихся
в системе на обслуживании и равно числу
занятых каналов.
Переход
системы из состояния
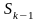в состояние
происходит при поступлении очередной
заявки с интенсивностью
=
,
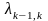а из состояния
в
- при обслуживании
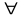из заявок в одном из k
каналов системы с интенсивностью
.
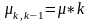Так как оба потока - входной и обслуживание – простейшие , то система является марковской , а процессы , в ней протекающие м.б. описаны как процессы размножения и гибели с помощью уравнений Колмогорова.
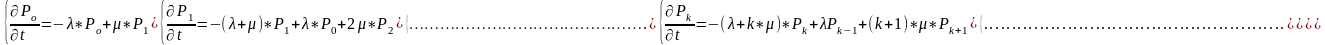
Решив данную систему диф. уравнений можно задать ???????????
Найти
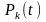- вероятность ,что в момент времени t
в сист. находится k
требований (занято k
каналов обслуживания).
Значение
финальных вероятностей найдем приравняв
=
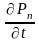0 и решив соответственно систему
алгебраических уравнений .
Используя найденные ранее выражения для финальных вероятностей – получим:
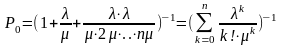
Обозначим
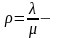приведённая
плотность потока заявок.
Его можно рассматривать как среднее число требований, приходящихся на среднее время обслуживания одного требования.
Тогда
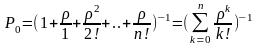
И вероятности состояний
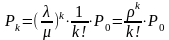
Дифференциальные уравнения, описывающие поведение системы без ожидания называются уравнениями Эрланга, а выражения для финальных вероятностей- формулами Эрланга- в честь основателя ТМО-датского учёного Эрланга, чьи исследования телефонных линий в начале 20 века, заложили основы современной ТМО.
Зная значения финальных вероятностей можно найти основные характеристики работы СМО в стационарном режиме.
1)Ротк-вероятность того, что требование получит отказ равно
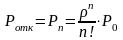
По формуле Литтла:
Средняя вероятность нахождения заявки в системе, равна средней вероятности обслуживания заявки в капом.
tсист=
отс
tсист=асист
=акон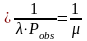
отс
акат=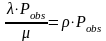
2)
Pобс=1-Ротк=1-Рn=1-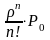
3) А- абсолютная пропускная способность системы( среднее число требований, обслуженных за единицу времени)
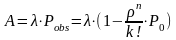
4) аn- среднее число занятых каналов
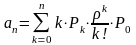
Так как найденный канал в единицу времени из А заявок, обнаруженных системой обслуживает ровно µ, то среднее число занятых каналов может быть найдено как
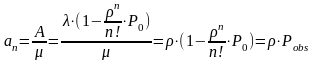
СМО с ожиданием.
Рассмотрим теперь другую задачу.
Имеется СМО с n каналами обслуживания. На вход системы поступает поток требований (заявок). В случае наличия свободного канала заявка поступает на обслуживание. Если в момент поступления заявки все каналы заняты, то заявка становится в очередь, ожидая пока освободится какой либо канал.
Такие системы называются системами с ожиданием. При этом время ожидания в очереди может быть как неограниченным («чистые системы с ожиданием»), так и ограниченным. Кроме того длина очереди может быть как неограничена, так и ограничена. В случае заполнения всей очереди пришедшие требования также получают отказ и не обслуживаются.
СМО с неограниченной очередью
Рассмотрим
СМО с неограниченной очередью и
неограниченным временем ожидания в
очереди. Поток требований на входе
системы- простейший с интенсивностью
ƛ. Продолжительность обслуживания
требования подчинена EXP
закону распределения со средним временем
обслуживания
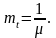Тогда система может рассматриваться
как марковская, вида M/M/n.
Изменение вероятностей состояния во
времени может быть записана с помощью
уравнений, расмножения и гибели.
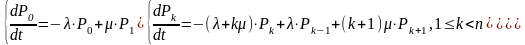
В этой системе при k<n интенсивность процесса «размножения» остается=ƛ, а интенсивность потока «гибели» не зависит от состояния и всегда равна nµ - интенсивности покидания требований из всех n каналов обслуживания.
Приравнивая
все
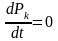для
стационарного режима получим выражения
для финальных вероятностей.
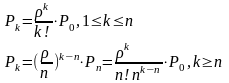
Где вероятность Ро ищется из нормирующего условия и равна
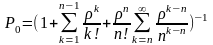
Условием
существования стационарного режима и,
соответственно, ненулевых
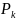
является сходимость бесконечного ряда в выражении для . Для этого необходимо , чтобы интенсивность процесса "размножения", начиная с K=n, была бы меньше , чем интенсивность процесса гибели , т.е.
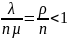
или ρ<n.
Если это условие не выполняется, то режима статического в СМО не существует, что приводит к неограниченному увеличению очереди. это условие необходимо обязательно учитывать при проектировании реальных СМО.
Если условие ρ/n<1 выполняется, то используя выражение для суммы членов бесконечной убывающей геометрической прогрессии получим для
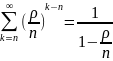
Отсюда
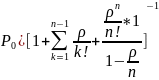
Найдем теперь основные характеристики СМО в стационарном режиме
1) Так как очередь не ограничена и все требования, поступающие в систему будут обнаружены, то
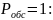
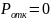
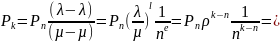
2. Пn – вероятность того, что все каналы обслуживания будут заняты
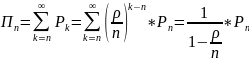
или через P0
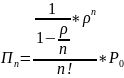
3. Среднее число занятых каналов
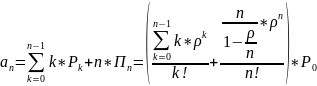
Т.к. все требования, поступающие в систему обслуживаются, то абсолютная пропускная способность системы A=λ (число требований обслуживаемых в системе в единицу времени). Отсюда среднее число занятых каналов можно найти как
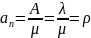
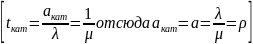
Т.е.
Стационарном режиме, при условии, что
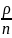<1
, т.е.
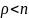среднее число занятых каналов всегда
равно ρ и не зависит
от n
4. Средняя длина очереди.
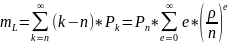
При
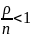ряд
сходится и равен
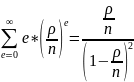
Отсюда средняя длина очереди будет равна
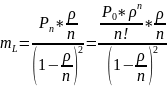
5. Среднее число требований, находящихся в системе будет равно
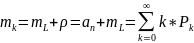
Это можно показать разбив Σ на 2 части: k < n и k ≥ n и представить во 2й части k=n+(k-n).
Используя формулу Литтла можно найти среднее время нахождения требования в очереди и в системе.
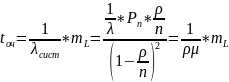
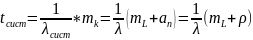
Отсюда
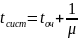
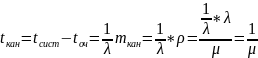
СМО с ограниченной длиной очереди.
Рассмотрим n канальную СМО с очередью, максимальная длина которой равна m. Время ожидания в очереди – не ограниченно.
Поток требований на входе в систему простейший с интенсивностью . Поток обслуживания также простейший с интенсивностью . В этом случае система будет марновской вида /m/n и изменения вероятностей состояния может быть описано с помощью уравнений размножения и гибели вида.
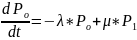
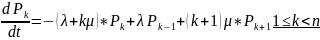
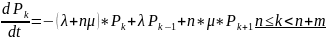
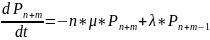
Т.к. число состояний СМО конечно, то в ней существует стационарный режим и выражения для финальных вероятностей могут быть записаны в следующем виде:
=
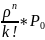1≤k≤n
=
*
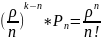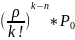n≤k≤n+m
Где
,
найденная из нормирующего условия
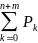=1
,будет равна
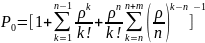
Учитывая, что вторая ∑ , как сумма членов геометрической прогрессии равна
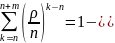
Получим окончательно.
Основные характеристики СМО в стационарном режиме будут:
1.Вероятность того, что пришедшее требование получит отказ.
*
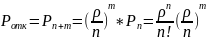2.Вероятность того, что пришедшее требование будет обслужено.
*
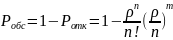3.Абсолютная пропускная способность системы(среднее число требований, обслуженной за единицу времени).
A=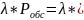
*
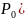
4. Вероятность того, что все каналы обслуживания заняты.
=
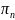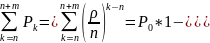
5.Среднее число занятых каналов.
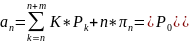
Или иначе через абсолютную пропускную способность системы:
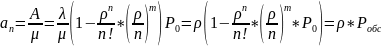
6.Средняя длина очереди.
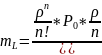
7.Среднее число требований к системе можно найти как
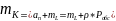
8.Среднее время нахождения требования в очереди
*
*
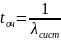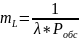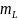
9.Общее время нахождения требования в системе будет
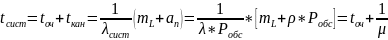
Полученные
….
решений носят общий характер. Положив
в них m=0
получим значения
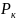и характеристики СМО для систем без
ожидания.
Положив м=∞ получим …… решения для СМО с неограниченным числом мест в очереди.
Пример.
Ателье обслуживает жителей 2-х микрорайонов.
Интенсивности заявок с обоих микрорайонов
равна
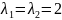чел/час. Среднее время исполнения
заявки=20 мин. Число работников в ателье
– 2 человека. Определить основные
характеристики работы ателье, если:
1)Очереди невозможны(m=0).
2)Очереди не ограничены (м=∞).
3. Как изменится эффективность работы если каждый из работников будет обслуживать клиентов только одного района.
1) m=0
а)
n=2;
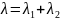=4;
µ=
;
;
;
*
=
;
*
=
;
=
=
;
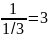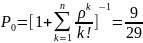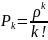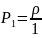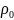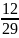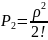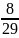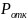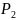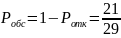=0,724;
A=
*
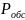=4*
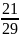=2,9;
;
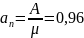б)
n=1,
=2;
µ=3;
;
*
;
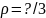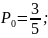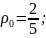
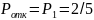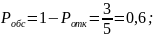
A= * =2*3/5=1,2;
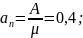
Как видим во 2-м случае снижается вероятность обслуживания каждого клиента, общее число обслуживаемых клиентов
А=2*1,2=2,4<2,9
Загрузка мастеров так же падает
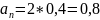<0,96.
2)
м=∞
a)n=2;
=4;
µ=3;
;
;
=
;
*
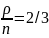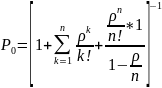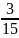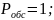
1≤k≤n ;
;
;
*
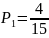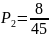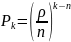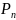k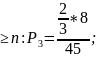
=
;
=
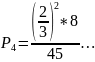
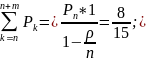
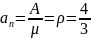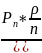=1,07;
*
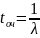