
Марковские случайные процессы .
Под случайным процессом понимают изменение во времени состояний некоторой физической системы заранее неизвестным случайным образом. При этом под физической системой будем понимать техническое устройство , группу устройств , предприятие , отрасль , биологическую систему и т.д.
Случайный процесс протекающий в системе называется Марковским – если для момента времени ,вероятностные характеристики процесса в будущем (t > ) зависят только от его состояния в данный момент времени
(в настоящем) и не зависят от того ,когда и как система пришла в это состояние в прошлом .
(Например счетчик Гейгера ,регистрирующий число космических частиц)
На практике Марковские процессы в чистом виде встречаются не часто . Однако нередко приходится иметь место с процессами , для которых влиянием предыстории можно пренебречь. Кроме того , если все параметры из «прошлого»,от которых зависит «будущее» включить в состоянии системы в «настоящем», то ее также можно рассматривать как Марковскую. Однако это приводит к значительному росту размерности ??????? переменных и невозможности получить решение задачи .
В исследование операций большое значение занимают т.н. Марковские случайные процессы с дискретными состояниями и непрерывным временем.
Процесс
называется процессом
с дискретными состояниями
, если все его возможные состояния
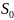 ,
,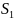 можно заранее ?????? (перенумеровать) .
Переход системы из состояния в состояние
переходит практически мгновенно
–скачком.
можно заранее ?????? (перенумеровать) .
Переход системы из состояния в состояние
переходит практически мгновенно
–скачком.
Процесс называется процессом с непрерывным временем ,если моменты перехода из состояния в состояние могут принимать случайное значение на временной оси .
Например: Техническое устройство S состоит из двух узлов , каждый из которых в случайный момент времени может выйти из строя (отказать). После этого мгновенно начинается ремонт узла (восстановление),который продолжается случайное время .
Возможны следующие состояния системы :
- оба узла исправны;
- первый узел ремонтируется ,второй исправен.
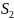 – второй
узел ремонтируется ,первый исправен
– второй
узел ремонтируется ,первый исправен
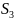 -
оба узла ремонтируются .
-
оба узла ремонтируются .
Переход системы из состояния в состояние происходит в случайные моменты времени практически мгновенно .Состояния системы и связь между ними удобно отобразить с помощью графа состояний .








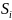
- состояния

- переходы
Переходы и отсутствуют т.к. отказы и восстановления элементов происходят независимо и случайно и вероятность одновременного выхода (восстановления ) двух элементов бесконечно мала и ?ей? можно пренебречь.
Если все потоки событий ,переводящие систему S из состояния в состояние –простейшие , то процесс протекающий в такой системе будет Марковским. Это обуславливается тем , что простейший поток не обладает последействием , т.е. в нем «будущее» не зависит от «прошлого» и кр. того , он обладает ?ординарности ? – вероятность одновременного появления двух и более событий бесконечно мала – т.е невозможен переход из состояния в состояние , минуя несколько промежуточных состояний.
Для
наглядности на графе состояний удобно
у каждой стрелки перехода проставить
интенсивность того потока событий,
который переводит систему из состояния
в состояние по данной стрелке (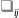 -интенсивность потока событий ,переводящего
систему из состояния
в
-интенсивность потока событий ,переводящего
систему из состояния
в
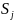 .
.
 такой граф называется размеченным
такой граф называется размеченным
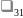
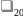
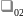
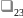
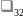
Используя размеченный граф состояний системы можно построить математическую модель данного процесса .
Обозначим
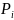 (t)-
вероятность
i-ого состояния системы
– вероятность того , что система в момент
времени t находится в состоянии
.
Для
момента t справедливо ?
(t)-
вероятность
i-ого состояния системы
– вероятность того , что система в момент
времени t находится в состоянии
.
Для
момента t справедливо ?
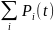 =1??
=1??
Пусть система в момент времени t находится в одном из состояний .
Определим вероятность того , что в момент времени t+∆ t система будет находится в состоянии . Это может быть в следующих случаях :
Система находилась в состоянии и за время ∆ t из него не вышла.
Это
означает ,что за время ∆
t не
возникло
события, переводящего систему в состояние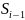 (поток с интенсивностью
(поток с интенсивностью
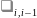 ) или события ,переводящего ее в состояние
) или события ,переводящего ее в состояние
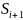 (поток с интенсивностью
(поток с интенсивностью
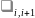 )
)
Можно показать ,что вероятность этого будет равна (при малых ∆ t)
P( / )=1 – ( + )* ∆ t
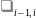
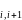
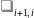
При экспоненциальном законе распределения времени между двумя соседними требованиями ?соответсвующем? простейшему потоку событий вероятность того, что на интервале времени ∆ t не возникнет ни одного требо вания в потоке с интенсивностью λ1 будет равна
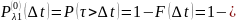
(см **)
Аналогично для потока с интенсивностью λ2
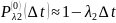
Вероятность, что не возникнет ни одного требования

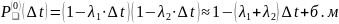
(см ***)
(2)
Система находилась в состоянии Si-1
и
за время
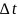 перешла в состояние Si
перешла в состояние Si
(т.е.
в потоке с интенсивностью
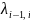 возникло хотя бы одно событие) Вероятность
этого равна для простейшего потока
возникло хотя бы одно событие) Вероятность
этого равна для простейшего потока

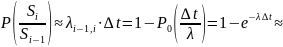
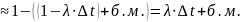
**
Разлагая функцию f(t) в ряд Тейлора (t>0) получим (для t=∆ t)
f(∆
t)=f(0)+ (0)*
∆
t +
(0)*
∆
t +
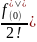 *∆
*∆
 +
+
 *∆
*∆
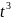 +…=
+…=
=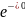 +(-)
*∆
t+
+(-)
*∆
t+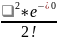 +(∆
+(∆
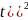 +
+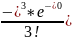 +(∆
+(∆
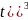 +…1-*∆
t
при
∆
t0
+…1-*∆
t
при
∆
t0
***
 (∆
t)/
(∆
t)/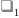 ???????????=
(∆
t/
???????????=
(∆
t/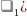 *
(∆
t/
*
(∆
t/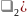 =(1-
*∆
t)(1-
=(1-
*∆
t)(1-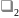 *∆
t)=
*∆
t)=
1-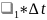 -
*∆
t+
-
*∆
t+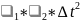 1-(
+
)*∆
t+б.м
при
∆
t0
1-(
+
)*∆
t+б.м
при
∆
t0
????????? = +
(∆ t/= + = 1-( + )*∆ t+б.м
(3) Система находилась в состоянии и за время ∆t перешла в состояние
Вероятность этого будет
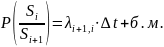
Тогда вероятность, что система в момент времени t+∆t будет в состоянии Si равна
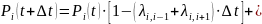
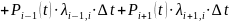
Вычтем из обеих частей Pi(t), разделим на ∆t и перейдя к пределу при ∆t→0, получим
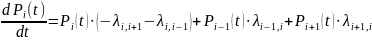
Подставив соответствующие значения интенсивностей переходов получим систему диф. уравнений, описывающих вероятности состояний системы как функции времени.(аргумент t-опустим).
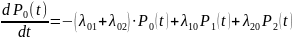
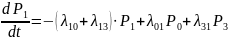
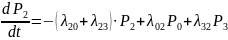
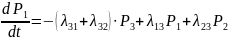
Данные уравнения называются уравнениями Колмогорова для дискретного Марковского процесса.
Задав начальные условия (напр. P0(t=0)=1, Pi(t=0)=0 i≠0) и решив их, получим выражения для вероятности состояния системы как функции времени. Аналитические решения достаточно просто получить, если число уравнений ≤ 2,3. Если их больше, то обычно решают уравнения численно- на ЭВМ. (напр. м. Рунге-Кутта).
В
теории случайных процессов доказано,
что если
число n
состояний системы конечно
и из каждого из них можно (за конечное
число шагов) перейти в
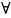 другое, то
существует предел,
к которому стремятся вероятности
другое, то
существует предел,
к которому стремятся вероятности
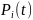 при t→
при t→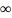 .
Такие вероятности наз-ся Финальными
вероятностями
состояний, а установившийся режим-
стационарным
режимом функционирования системы.
.
Такие вероятности наз-ся Финальными
вероятностями
состояний, а установившийся режим-
стационарным
режимом функционирования системы.
Т.к.
в стационарном режиме все
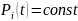 ,
следовательно все
,
следовательно все
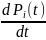 =0
=0
Приравняв в системе уравнений левые части 0 и, дополнив их уравнением
 =1
получим систему линейных алгебраических
уравнений, решив которую найдём значения
Финальных вероятностей.
=1
получим систему линейных алгебраических
уравнений, решив которую найдём значения
Финальных вероятностей.
Пример Пусть в нашей системе интенсивности отказов и восстановления элементов следующие
Отказы
1эл:
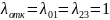
2эл:
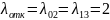
Ремонт
1эл:

2эл:
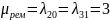
P0+P1+P2+P3=1
0=-(1+2)P0+2P1+3 P2
0=-(2+2)P1+1P0+3P3
0=-(1+3)P2+2P0+2P3
0=-(2+3)P3+2P1+1P2
Решив систему получим
P0=6/15=0.4; P1=3/15=0.2; P2=4/15=0.27; P3=2/15≈0.13
Т.е. в стационарном состоянии система в среднем
40% находится в состоянии S0 (оба узла исправны),
20%- в состоянии S1 (1-й эл-т ремонтируется, 2-й исправен),
27%- в состоянии S2 (2-й эл-т………., 1…….),
13%- в состоянии S3 – оба эл-та в ремонте.
Знание финальных вероятностей позволяет оценить среднюю эффективность работы системы и загрузку службы ремонта.
Пусть система в состоянии S0 приносит доход 8 усл.ед. в единицу времени; в состоянии S1-доход 3 усл.ед.; в состоянии S2- доход 5;в состоянии S3-доход=0
Стоимость ремонта в единицу времени для эл-та 1- 1(S1,S3) усл.ед., эл-та 2- (S2,S3) 2 усл.ед. Тогда в стационарном режиме:
Доход сист. в единицу времени будет:
Wдох=8P0+3P1+5P2+0P3=8·0.4+3·0.2+5·0.27+0·0.13=5.15 усл.ед.
Стоимость ремонта в ед. времени:
Wрем=0P0+1P1+2P2+(1+2)P3=0·0.4+1·0.2+2·0.27+3·0.13=1.39 усл.ед.
Проведя определённые расходы можно изменить интенсивности λ и μ и соотв-но эффективность системы. Целесообразность таких расходов можно оценить, проведя пересчёт Pi .
Прибыль в единицу времени
W= Wдох- Wрем=5.15-1.39=3.76 усл.ед
Процессы размножения и гибели.
Как видно из предыдущего в случае, если для системы S имеется размеченный граф состояний, то для нее легко могут быть составлены уравнения Колмогорова, на основании которых рассчитывают значения финальных вероятностей состояния системы.
Общий интерес имеет случай, когда граф состояний системы представляет собой так называемую «схему размножения и гибели». В этом случае для финальных вероятностей удается получить достаточно простые выражения.
Для схемы размножения и гибели граф состояний системы имеет вид:
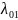
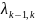
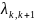
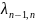

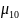
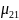
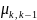
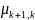
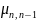
Особенность
его
в том, что все состояния системы можно
втянуть в одну цепочку, в которой каждое
из средний стояний S-Sn-1
связано с соседними состояниями справа
и слева прямой и обратной стрелкой(переходом),а
крайние состояния
и
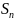 только
с одним соседним состоянием.
только
с одним соседним состоянием.
Термин
«схема размножения и гибели» берет
начало от биологических задач, где
подобной схемой описывается изменение
численности популяции. Процесс размножения
и гибели соответствует как бы двум
потокам: «размножение»-переход от
состояния
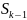 к
к
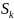 с интенсивностью
за счет возникновения требований в
системе и «гибели»-переход от
с интенсивностью
за счет возникновения требований в
системе и «гибели»-переход от
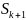 к
с интенсивностью
к
с интенсивностью
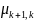 – за счет убивания («обслуживания»)
требований.см *.
– за счет убивания («обслуживания»)
требований.см *.
Пусть все потоки событий, переводящие систему S из состояния в состояние –простейшие. Тогда уравнение Колмогорова для неё могут быть записаны в виде:
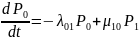
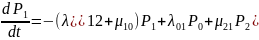
…

…
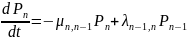
Для
стационарного состояния при
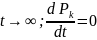
Их можно записать в след. виде:
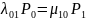
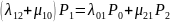
…
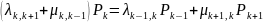
…
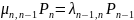
Подставив каждое предыдущее уравнение в последующее поучим:

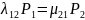
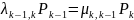
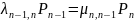
Каждое из уравнений системы характеризует баланс «прямых» и «обратных» потоков из состояния в состояние с учетом вероятностей состояний.
Выразим из них вероятности всех последующих состояний через предыдущее:
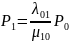
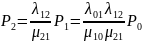
…
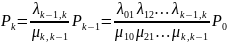
…
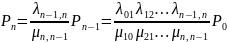
Т.о.
все финальные вероятности состояний
системы можно выразить через интенсивность
потоков и вероятность начального
состояния
.
Дополнив систему нормирующим условием
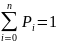 получим:
получим:
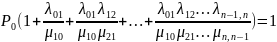

В случае, если в системе существуют только потоки требований «вперед»,т.е. за счет их возникновения, то процесс рассматривается как «процесс чистого размножения».
Если измерение состояний системы происходит только «назад», за счет обнуления требований ,то говорят о «процессе чистой гибели».
Формула Литтла .
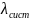
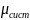

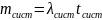
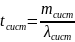
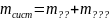
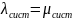
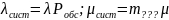

Отсюда получим выражение для P0
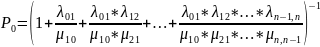
Или
…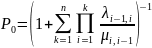
Если число состояний n конечно, то ряд, стоящий в …. для P0 –сходится и следовательно вероятности P0и Pk (1 ≤k≤n) отличны от нуля.
Если же число возможных состояний n системы неограниченно (n = ∞), то ряд может расходиться. В этом случае P0и остальные Pk (k> 0) будут = 0 и режима статического равновесия в процессе не существует.
Для
того,чтобы
режим статического равновесия существовал
необходимо, чтобы
ряд в P0сходился.
Для этого необходимо, чтобы начиная с
некот. i0выполнялось
условие
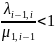 i>i0
i>i0
т.е. интенсивность процесса «гибели» была выше , чем интенсивность процесса размножения. В противном случае номер состояния K системы будет неуклонно возрастать.
Для стационарного режима вероятности Pkбудут равны
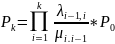 1
< k < n
1
< k < n
Определение основных характеристик СМО
Рассмотрим СМО вида
Выходной поток
2
1




. . .
Очередь

