Министерство образования Российской Федерации

Томский Государственный

Архитектурно-Строительный

Университет

Кафедра «жбк»

Курсовой проект №1.

«Многоэтажное промышленное здание»

Выполнил:

Студент: гр.119-2

Калиничев Д. А.

Проверил:

Саркисов д.Ю.

Томск – 2012

Этап I

Данные для проектирования.

Шаг колонн в продольном направлении, м	5,80
Врем. нормат. нагр. на перекрытие, кн/м2	6,40
Пост. нормат. нагр. от массы пола, кн/м2	0,80
Класс бетона для сборных конструкций	В 30
Класс предв. напрягаемой арматуры	А-VI
Способ натяжения арматуры на упоры	Эл.терм.
Условия твердения бетона	Естественные
Тип плиты перекрытия	Овал.
Вид бетона для плиты	Тяжелый
Влажность окружающей среды	80 %
Класс ответственности здания	I

Решение.

По результатам компоновки конструктивной схемы перекрытия принята номинальная ширина плиты 1200 мм. Расчетный пролет плиты при опирании на ригель поверху

l₀=l-b/2=5800-250/2=5675 мм.

Подсчет нагрузок на 1м² перекрытия приведен в табл. 1.

Таблица 1.

Нагрузки на 1м² перекрытия

Вид нагрузки	Нормативная нагрузка кН/м2	Коэффициент надежности по нагрузке	Расчетная нагрузка, кН/м2
Постоянная: -от массы плиты	0,092  25 =2,3	1,1	2,53
-от массы пола (по зданию)	0,8	1,2	0,96
Итого:	3,1	-	3,49
Временная (по зданию) в том числе:	4	1,2	4,8
Длительная	2,5	1,2	3,0
Кратковременная	1,5	1,2	1,8
Полная нагрузка	7,1	-	8,29
В том числе постоянная и кратковременная	5,6	-	-

Расчетные нагрузки на 1м² длины при ширине плиты 1,0 м, с учетом коэффициента надежности по назначению здания .

для расчетов по I группе предельных состояний

q = 8,29  1,2  1 = 9,948 кН/м

для расчетов по II группе предельных состояний

полная q_tot = 7,1 1,2  1 = 8,52 кН/м

длительная q_L = 5,6  1,2  1 = 6,72 кН/м

Расчетные усилия: для расчетов по I группе предельных состояний

M = ql₀²/8 = 9,948  5,675²/8=40,05кНм

для расчетов по второй группе предельных состояний

Нормативные и расчетные характеристики легкого бетона класса B30, твердеющего в естественных условиях при атмосферном давлении, (для влажности 80%): MПа; MПа; МПа; МПа; МПа.

Нормативные и расчетные характеристики напрягаемой арматуры класса А-VI: МПа; МПа; МПа.

Н азначаем величину предварительного напряжения арматуры: Мпа.

Проверим условие при Мпа (для электротермического способа натяжения). Так как Мпа,<R_s,ser=980Мпа, а Мпа>0,3∙R_s,ser = 294Мпа следовательно, условие выполняется.

Предварительное напряжение при благоприятном влиянии с учетом точности натяжения арматуры будет равно Мпа, где принемаем 0,1

Расчет плиты по предельным состояниям первой группы.

Расчет прочности плиты по сечению, нормальному к продольной оси, M=40,05 кНм. Сечение тавровое с полкой в сжатой зоне. Согласно п. 3.16 СниП 2.03.01-84 при расчетная ширина полки . . Проверяем условие Нмм =87,51кНм > >M=40,05 кНм, т.е. граница сжатой зоны проходит в полке, и расчет производим как для прямоугольного сечения шириной мм.

Определим значение ; находим и .

Вычеслим относительную граничную высоту сжатой зоны по формулам п.3.12[2] Находим характеристику сжатой зоны бетона , где α=0,85 для тяжелого бетона.

Тогда , где Мпа; предварительное напряжение принято с учетом полных потерь равным Мпа; так как Мпа<0, то Мпа при

Находим коэффициент условий работы, учитывающий сопротивление напрягаемой арматуры выше условного предела текучести принимаем

Вычислим требуемую площадь сечения растянутой напрягаемой арматуры:

мм². Принимаем 410 А-VI (A_sp=314 мм²).

Расчет полки плиты на местную прочность.

Расчетный пролет, согласно рис.1.15, а, l₀=355мм. Нагрузка на 1 м² полки толщиной 25мм будет равна кН/м²

Изгибающий момент для полосы шириной 1м определяем с учетом частичной заделки в ребрах по формуле кН м;

Размещаем арматурную сетку в середине сечения полки, тогда мм. Находим ;

Назначаем диаметр рабочей арматуры сетки 3 мм класса Вр-I (R_s=375Мпа) и вычисляем требуемую площадь рабочей арматуры мм². Принимаем сетку с поперечной рабочей арматурой ᴓ3 Вр-I с шагом s=200мм

(5ᴓ3,A_s=35,5мм²)

Проверка прочности плиты по сечениям, наклонным к продольной оси, Q_max=28,23 кН; q₁=q=9.948 кН/м. Проверяем условие. Так как > Q_max=28.23 кН, то условие выполняется.

Проверим условие, принимая приблеженно значение Q_b1=Q_b,min и м. Находим усилие обжатия от растянутой продольной арматуры ;

Вычисляем следовательно =0,373; - для тяжелого бетона.

Тогда . Q_b1=Q_b,min=29,21кН. Поскольку , то для прочности наклонных сечений не требуется поперечная арматура.

Расчет плиты по предельным состояниям второй группы.

Пустотная плита, эксплуатируемая в закрытом помещении и армированная напрягаемой арматурой класса A-VI диаметром 10 мм, должна удовлетворять 3-й категории требований по трещиностойкости, т.е. допускается непродолжительное раскрытие трещин шириной a_crc1=0.3мм и продолжительное – a_crc2=0.2мм. Прогиб плиты от действия постоянной и длительной нагрузок не должен превышать f_u=0,0284 м.

A_red=1028 см²;

Y₀=11,5 cм;

I_red=70062 см⁴;

^;

^;

^;

^;

Z=16,8 см;

Z_L=16,2 см;

b=20,52 см;

Определяем первые потери предварительного напряжения арматуры:

- потери от релаксации напряжений в арматуре ;

- , так как форма нагревается вместе с изделием;

- и при заданном электротермическом способе натяжения;

-поскольку напрягаемая арматура не отгибается, потери от трения арматуры ;

Таким образом, усилие обжатия P₁ с учетом потерь равно P₁=( кН.Точка приложения усилия P₁ совпадает с центром тяжести сечения напрягаемой арматуры, поэтому e_op = Y₀ - a =115-30 = 85 мм.

Определим потери от быстронатекающей ползучести бетона, для чего вычислим напряжение в бетоне в середине пролета от действия силы P₁ и изгибающего момента M_w от собственной массы плиты.

Нагрузка от собственной массы плиты равна q_w=2,3·1,2=2,76 кН/м, тогда

Напряжение на уровне растянутой арматуры (т.е. при y = e_op =85 мм)

=1,832 МПа.

Напряжение на уровне крайнего сжатого волокна (т.е. при y = h - y₀= 220–115=105 мм): =1,118 МПа.

Назначаем передаточную прочность бетона .

Тогда потери от быстронатекающей ползучести бетона будут равны:

на уровне арматуры <0.8; поскольку , то ;

на уровне крайнего сжатого волокна , то .

Следовательно, первые потери составляют , и соответствующее усилие обжатия будет равно P₁=( .

Определим максимальное сжимающее напряжение в бетоне от действия силы P₁ без учета собственной массы, принимая y=y₀=115 мм:

.

Поскольку требование удовлетворяется.

Определим вторые потери предварительного напряжения:

Потери от усадки .

Для определения потерь от ползучести бетона вычислим напряжения в бетоне от усилия P₁:

на уровне растянутой арматуры

;

на уровне крайнего сжатого волокна

;

Так как , то .

Так как , то . Тогда вторые потери составят , соответственно суммарные потери будут равны принимаем =100Мпа

Усилие обжатия с учетом суммарных потерь составит P₂=( .

Произведем проверку образования трещин в плите.

При действии внешней нагрузки в стадии эксплуатации максимальное напряжение в сжатом бетоне равно:

=4,669 МПа,

тогда принимаем и получим .

При действии усилия обжатия Р₁ в стадии изготовления максимальное напряжение в сжатом бетоне равно:

=2,46 МПа,

При этом можно видеть, что минимальное напряжение в бетоне в стадии изготовления, равное т.е. будет сжимающим. Следовательно, верхние начальные трещены заведомо не образуются, и образование нижних трещин проверяем без учета коэффициента Ɵ.

Принемаем M_r=M_tot=34,3кН*м. Определяем момент трещинообразования в нижней зоне плиты ; где .

Так как M_crc=36,36 кН·м>M_tot=34,3 кН·м, то трещины в растянутой зоне не образуются и расчет по раскрытию трещин не нужен.

Расчет прогиба плиты расчитываем от действия постоянной и длительной нагрузок (M=M_l=27,05 кН·м, =0,85, =1,6).

Вычисляем прогиб:

Неразрезной ригель.

Методические указания. Неразрезной ригель многопролетного перекрытия представляет собой элемент рамной конструкции. При свободном опирании концов ригеля на наружные стены и равных пролетах ригель можно рассматривать как неразрезную балку. При этом возможен учет пластических деформаций, приводящих к перераспределению и выравниванию изгибающих моментов между отдельными сечениями.

Шаг колонн в продольном направлении, м	5,8
Шаг колонн в поперечном направлении, м	6,4
Число пролетов в поперечном направлении	4
Врем. нормат. нагр. на перекрытие, кН/м2	4,0
Пост. нормат. нагр. от массы пола, кН/м2	0.8
Класс бетона для сборных конструкций	В30
Класс арм-ры свободных ненапр. конструкций	А-III
Тип плиты перекрытия	Овал.
Вид бетона для плиты	тяжелый
Влажность окружающей среды	80%
Класс ответственности здания	I

Решение. Назначаем предварительные размеры поперечного сечения ригеля. Высота сечения h=600мм. Ширина сечения ригеля b=250мм.

Вычисляем расчетную нагрузку на 1 м длины ригеля. Нагрузка на ригеле от многопустотных плит считается равномерно распределенной. Ширина грузовой полосы на ригель равна шагу колонн в продольном направлении здания 6м.

Постоянная нагрузка на ригель будет равна:

от перекрытия (с учетом коэффициента надежности по назначению здания ) 3.49·5,8·1=20,24 кН/м.

от веса ригеля (сечение 0.25х0.6м, плотность железобетона , с учетом коэффициентов надежности =1.1 и ), 0.25 · 0.60 · 25 · 1.1 · 1=4.125кН/м.

g=20,24+4.125=24,367 кН/м.

Временная нагрузка: v=4,8·5,8=27,84 кН/м

Полная нагрузка q=g+v=52,21 кН/м.

Характеристики бетона и арматуры для ригеля.

Бетон тяжелый класса В30, =1 (при влажности 80%), R_b = 17 МПа, R_bt = 1,2МПа. Продольная рабочая арматура класса A-III, R_s=365 МПа. Находим ξ_r = 0,541 и α_r= =0,395.

Расчет прочности ригеля по сечениям, нормальным к продольной оси.

Сечение в пролете, М=196,4 кН·м, h₀=500-60=440 мм. Вычисляем α_m = М/(R_b·b·h₀²) = 0,328< α_r=0,395, следовательно, сжатая арматура не требуется. Находим ζ=0,793, тогда требуемую площадь растянутой арматуры определим А_s = M/(R_sζh₀) = 1542 мм². Принимаем 6Ø20 A-III (A_s=1885 мм²).

Сечение на опоре, М = 132,9 кН·м, h₀=500-45=455 мм, α_m=132,9·10⁶/(17·200·455²)=0,189< <α_r=0,395; ζ=0,895, тогда A_s=132,9·10⁶/(365·0,895·455)=894 мм². Принимаем 2Ø25 (A_s=982 мм²).

Монтажную арматуру принимаем 2Ø12 A-III (A_s=226 мм²)

Расчет прочности ригеля по сечениям, наклонным к продольной оси, Q_max=180,5 кН, q₁=q=52,21 кН/м (Н/мм).

Определим требуемую интенсивность поперечных стержней из арматуры класса A-I (R_sw=175 МПа, E_s=210000 МПа), принимая в опорном сечении h₀ =470 мм; φ_f=0, φ_b2=2 получим M_b= φ_b2·R_bt·b·h₀² = 106,032 кН·м.

Находим Q_b1 = 2 = 148,81кН. Так как Q_b1/0,6=248,02 кН > Q_max=180,5 кН, то требуемую интенсивность поперечных стержней определим q_sw=(Q²_max-Q²_b1)/(4·M_b)=24,61 кН/м.

Поскольку (Q_max-Q_b1)/(2h₀)=33,71 кН/м > q_sw=24,61 кН/м, то принимаем q_sw=33,71кН/м.

Проверяем условие Q_b,min=φ_b3·R_bt·b·h₀=67,68 кН, так как q_sw=33,71 кН/м< Q_b,min/(2h₀)=72 кН/м, то корректируем значение q_sw по формуле:

q_sw= 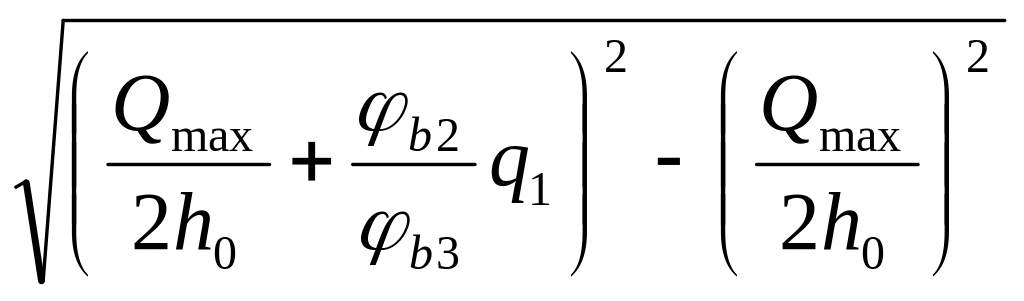=54,41 кН/м.

Шаг s₁ у опоры должен быть не более h/3 =500/3 = 167 мм и 500 мм, а в пролете — 3/4h = =375 мм и 500 мм. Максимально допустимый шаг у опоры будет равен s_max=φ_b4·R_bt·b·h₀²/Q_max= =440,58 мм.

Принимаем шаг поперечных стержней у опоры s₁=160 мм, а в пролете s₂=400 мм, отсюда А_sw=q_sw·s₁/R_sw=49,75 мм²; принимаем в поперечном сечении два поперечных стержня диаметром по 6 мм с учетом диаметра продольной арматуры (А_sw=57 мм²).

Таким образом, принятая интенсивность поперечных стержней у опоры и в пролете будет равна: q_sw1=А_sw·R_sw/s₁=62,34 Н/мм; q_sw2=24,94 Н/мм.

Так как q_sw1=62,34 Н/мм < Q_b,min/(2h₀)=72 Н/мм, а q_sw2=24,94 Н/мм < Q_b,min/(2h₀)=72 Н/мм, то корректировать значения М_b и Q_b,min не надо.

Вычисляем 1,3м>2h₀=0,94м принимаем 0,94м. Поскольку q₁=52,21кН/м<1,56q_sw1-q_sw2=72,31кН/м

2,68м

Но не более принимаем с=1,57м

l₁= 0,63 м.

Тогда L₁=l₁ + 0,2 м = 0,83 м < 1/4l=1,6 м, принимаем L₁=1,6 м.

Проверяем прочность по наклонной полосе ригеля между наклонными трещинами: μ_w=A_sw/(bs) = 0,0018; α=E_s/E_b=210000/32500=6,46; φ_w1=1+5αμ_w=1,06; φ_b1=1-βR_b=0,83; тогда 0,3·φ_w1·φ_b1·R_b·b·h₀=421,78 кН > Q_max=180,5 кН, , прочность наклонной полосы обеспечена.

Определяем изгибающие моменты, воспринимаемые в расчетных сечениях, по фактически принятой арматуре.

Сечение в пролете с продольной арматурой 3Ø 20 A-III, A_s = 942 мм²; x = R_sA_s/(R_bb) = =101,13 мм, ξ = x/h₀ = 0,215 < ξr = 0,541; тогда М = R_sA_s·(h₀-0,5x) = 144,21 кН·м.

Сечение в пролете с продольной арматурой 6Ø 20 A-III A_s = 1885 мм²; x = R_sA_s/(R_bb) = =202,36 мм, ξ = x/h₀ = 0,46 < ξr = 0,541; тогда М = R_sA_s·(h₀-0,5x) = 233,12 кН·м.

Сечение в пролете с арматурой в верхней зоне 2Ø12 A-III A_s = 226 мм²; x = R_sA_s/(R_bb) = =24,26 мм, ξ = x/h₀ = 0,052 < ξr = 0,541; тогда М = R_sA_s·(h₀-0,5x) = 37,15 кН·м.

Сечение у опоры с арматурой в верхней зоне 2Ø25 A-III A_s = 982 мм²; x = R_sA_s/(R_bb) = =105,42 мм, ξ = x/h₀ = 0,228 < ξr = 0,541; тогда М = R_sA_s·(h₀-0,5x) = 146,88 кН·м.

Пользуясь полученными значениями изгибающих моментов, гра­фическим способом находим точки теоретического обрыва стержней и соответствующие им значения поперечных сил.

Вычисляем необходимую длину анкеровки обрываемых стержней для обеспечения прочности наклонных сечений на действие изгибающих моментов.

Для нижней арматуры по эпюре Q графическим способом находим поперечную силу в точке теоретического обрыва стержней диаметром 20 мм Q=76,9 кН, тогда требуемая длина анкеровки будет равна w₁ = Q/(2q_sw) + 5d = 806 мм = 81 см. Для верхней арматуры у опоры диаметром 25 мм при Q=65,5 кН соответственно получим w_b=73 см.

Монолитное ребристое перекрытие с балочными плитами.

Назначаем предварительно следующие значения геометрических размеров элементов перекрытия:

высота и ширина поперечного сечения второстепенных балок

h = (1/12... 1/20)l = 1/14·5700 =400 мм, b= (0,3 ... 0,5)/h = 0,5 · 400 = 200 мм;

высота и ширина поперечного сечения главных балок

h=(1/8... 1/15)l = 1/12·7000 = 450 мм, b = 250 мм;