Толщину плиты примем 80 мм при максимальном расстоянии между осями второстепенных балок 2200 мм. Вычисляем расчетные пролеты и нагрузки на плиту. Получим в коротком направлении

l₀₁=l - b/2 - с + а/2 = 2000 - 200/2 - 250 + 120/2 = 1710 мм; l₀₂ =l - b = 2200 - 200 = 2000 мм; а в длинном направлении l₀=l – b = 5800 - 250 = 5550 мм.

Поскольку отношение пролетов 5550/2000 = 2,8 > 2, то плита балочного типа.

Для расчета плиты в плане перекрытия условно выделяем полосу шириной 1 м. Плита будет работать как неразрезная балка, опорами которой служат второстепенные балки и наружные кирпичные стены. При этом нагрузка на 1 м плиты будет равна нагрузке на 1 м² перекрытия.

Нагрузки на 1 м² плиты монолитного перекрытия

Вид нагрузки	Нормативная нагрузка, кН/м	Коэффициент надежности по нагрузке	Расчетная нагрузка, кН/м
Постоянная: от массы плиты (h = 0,08 м; p = 25 кН/м3) от массы пола	0,08·25=2,00 0,8 2,8 4,0 6,8	1,1 1,2 1,2	2,20 0,96 q=3,16 v=4,8 7,96
Итого Временная
Всего

С учетом коэффициента надежности по назначению здания расчетная нагрузка на 1 м плиты q=(g+v) · = 7,96·1=7,96 кН/м.

Определим изгибающие моменты с учетом перераспределения усилий:

в средних пролетах и на средних опорах

М=ql /16 = 7,96·2² /16 = 1,99 кН·м;

в первом пролете и на первой промежуточной опоре

M=ql /11= 7,96·1,71²/11=2,12 кН·м.

Так как для плиты отношение h/l =80/2000=1/25 > 1/30, то в средних пролетах, окаймленных по всему контуру балками, изгибающие моменты уменьшаем на 20 %, т. е. они будут равны 0,8 · 1,99 = 1,59 кН·м.

Определим прочностные и деформативные характеристики бетона заданного класса с учетом влажности окружающей среды.

Бетон тяжелый, естественного твердения, класса В20, при влажности 80%: =1; R_b=11,5МПа; R_bt = 0,9МПа; E_b=27000 МПа.

Выполним подбор сечений продольной арматуры сеток. В средних пролетах, окаймленных по контуру балками и на промежуточных опорах: h₀=h - а = 80 – 12,5 = 67,5 мм, α_m = М/(R_b·b ·h₀²)= =1,59·10⁶/(11,5·1000·67,5²) = 0,03; ξ = 0,03 < ξr = 0,59 , ζ=0,985, тогда R_sA_s =М/(ζh₀) = 23914 Н; принимаем сетку С1 номер 10 марки с фактической несущей способностью продольной арматуры R_sA_s = 25550 Н > 23914 Н.

В первом пролете и на первой промежуточной опоре: h₀ = 80 - 16,5 = 63,5 мм; α_m = М/(R_b·bx xh₀²) = 0,046; ξ = 0,047 < ξr, ζ=0,977, тогда R_sA_s =М/(ζh₀) = 34172 Н; дополнительная сетка должна иметь несущую способность продольной арматуры не менее 34172-25550 = 8622 Н; принимаем сетку С2 номер 31 марки с R_sA_s=18110Н > 8622 Н.

Расчет второстепенной балки. Вычисляем расчетный пролет для крайнего пролета балки, который равен расстоянию от оси опоры на стене до грани главной балки:

l₀₁ = l-c/2 - b/2 = 5800 - 250/2 - 250/2 = 5550 мм = 5,55 м.

Определим расчетную нагрузку на 1 м второстепенной балки, собираемую с грузовой полосы шириной, равной максимальному расстоянию между осями второстепенных балок (2,2 м).

Постоянная нагрузка:

от собственного веса плиты и пола (см. расчет плиты) 3,16·2,2=6,952 кН/м;

от веса ребра балки 0,2(0,4 - 0,08)25·1,1 = 1,76 кН/м;

Итого: g = 8,71 кН/м.

Временная нагрузка: v = 5,8·2,2 = 12.76 кН/м.

Итого с учетом коэффициента надежности по назначению здания: q=(g+v)· = 21,47 кН/м.

Изгибающие моменты с учетом перераспределения усилий в статически неопределимой системе будут равны:

в первом пролете M=ql /11 = 21,47·5,55² /11 = 60,12 кН·м;

на первой промежуточной опоре М=ql /14=47,24 кН·м.

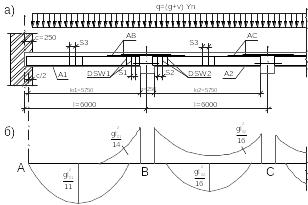
a — схема армирования; б — эпюра изгибающих моментов

Максимальная поперечная сила (на первой промежуточной опоре слева) равна Q=0,6ql = =0,6·21,47·5,55 = 71,5 кН.

Согласно задания продольная рабочая арматура для второстепенной балки класса A-II (R_s= =365 МПа).

Проверим правильность предварительного назначения высоты сеч-я второстепенной балки:

ho = =266 мм, или h₀+а = 266+35 = 301мм < 400 мм, т. е. высоту сечения увеличивать не требуется.

Выполним расчеты прочности сечений, нормальных к продольной оси балки, на действие изгибающих моментов.

Сечение в пролете М=60,12 кН·м. Определим расчетную ширину полки таврового сечения: при h /h = 80/400=0,2>0,1 и 2·1/6·l +b = 2050 мм < 2200 мм (расстояние между осями второстепенных балок) принимаем b = 2050 мм. Вычислим h₀ = h – а = 400 – 30 = 370 мм.

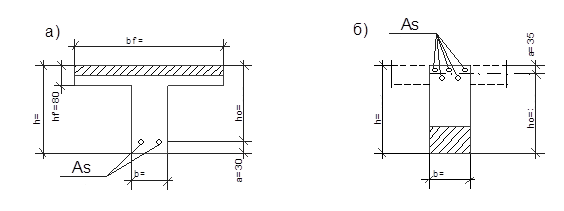
К расчету продольной арматуры в сечениях второстепенной балки:

а) – в пролете; б) – на опоре.

Так как R =11,5·2050·80·(370-0,5·80) = 622,38 кН·м > М = 60,12 кН·м, то граница сжатой зоны проходит в полке, и расчет производим как для прямоугольного сечения шириной b= = 2050 мм. Вычислим α_m=М/(R_sbh₀) = 60,12·10⁶/(11,5·2050·370²) = 0,019 < α_r = 0,416. По α_m=0,019 находим ζ=0,991, тогда требуемая по расчету площадь продольной рабочей арматуры будет равна А =М/(R_sζh₀) = 449 мм². Принимаем 3Ø14 A-III (А =462 мм²).

Сечение на опоре В: М = 47,24 кН·м. Вычислим h₀ = h-а = 400-35 = 365 мм. Вычислим α_m= =М/(R bh ) = 0,154 < α_r = 0,416, т.е. сжатая арматура не требуется. По α_m=0,154 находим ζ=0,916, тогда А_s=М/(R_sζh₀) = 369 мм². Принимаем 5Ø10 A-III (А_s= 393 мм²).

Выполним расчет прочности наиболее опасного сечения балки на действие поперечной силы у опоры В слева. Из условия сварки принимаем поперечные стержни диаметром 4 мм класса Bp-I (R_sw=265 МПа, Е_s=170000 МПа), число каркасов – 2 (А_sw = 2·12,6 = 25,2 мм²). Назначаем максимально допустимый шаг поперечных стержней s = 150 мм согласно требованиям.

Поперечная сила на опоре Q_max= 71,5 кН, фактическая равномерно распределенная нагрузка q₁=21,47кН/м.

Проверим прочность наклонной полосы на сжатие. Определяем коэффициенты и = 25,2/(200·150)=0,00084; α=E_s/E_b =6,3; отсюда = 1 + 5α = 1+ 5·6,3·0,00084= =1,03 < 1,3; для тяжелого бетона β = 0,01; 1 – 0,01·11,5 = 0,885.

Тогда 0,3 =0,3·1,03·0,885·11,5·200·370 = 232,72кН > Q_max=71,5 кН, т.е. прочность наклонной полосы ребра балки обеспечена.

Проверим прочность наклонного сечения по поперечной силе. Определим величины М_b и q_sw: =2; так как =2050-200=1850 мм > =3·80=240 мм, принимаем =240 мм, тогда =0,75 )=0,195 < 0,5,

Определим значение Q_b,min принемая

Поскольку Q_b,min/h₀=64,53кН/м > q_sw=44,52кН/м следовательно корректируем значение M_b.

Определяем длину проекции опасного наклонного сечения с. Так как 0,5бq_sw=24,93 кH/м > q₁= 21,47 кН/м, значение с определяем только по формуле с= =1,38 м. Поскольку с=1,38 м> > =(2/0,6)·0,37=1,23 м, принимаем с=1,23 м.

Тогда Q_b=M_b/c= 40,63/l,23 =33,03 кН< Q_b,min=47,75кН; Принимаем Q_b=Q_b,min=47,75кН Q=Q_max–q₁·c=71,5 – 21,47·1,23 = 45,09 кН.

Длина проекции наклонной трещины будет равна: с₀= =0,955 м. Так как с₀=0,955м>2h₀= 2·0.37 = 0,74 м, принимаем с₀ = 0,74 м, тогда Q_sw= q_sw·с₀= 32,95 кН.

Проверим условие Q_sw+Q_b = 80,7 кН > Q = 45,09 кН, т. е. прочность наклонного сечения по поперечной силе обеспечена.

Требования выполняются, поскольку =517 мм > s =150 мм.

Сборная железобетонная колонна и центрально нагруженный фундамент под колонну.

Решение. Определим нагрузку на колонну с грузовой площади, соответствующей заданной сетке колонн 6,4·5,8=37,12 м² и коэффициентом надежности по назначению здания =1.

Постоянная нагрузка от конструкций одного этажа:

от перекрытия 3,49 ·37,12·1=129,55 кН;

от собственного веса ригеля сечением 0,2x0,5 м длиной 6,4 м при плотности железобетона =25 кН/м³ и =1,1 будет равна 0,2·0,5·6,4·25·1,1·1 = 17,6кН;

от собственного веса колонны сечением 0,3x0,3 м при высоте этажа 3,3м составит 0,3·0,3·3,3·25·1.1·1=8,17 кН.

Итого: 129,55+17,6+8,17 = 155,32 кН.

Временная нагрузка от перекрытия одного этажа 4,8·37,12·1=178,176 кН, в том числе длительная – 3·37,12·1=111,36 кН.

Постоянная нагрузка от покрытия при нагрузке от кровли и плит 5 кН/м² составит 5·37,12·1=185,6 кН, то же с учетом нагрузки от ригеля и колонны верхнего этажа 185,6+17,6+8.17=211,37 кН.

Временная нагрузка от снега для г. Саратов ( III снеговой район, =1 кН/м²) при коэффициенте надежности по нагрузке =1,4 будет равна 1·1,4·37,12·1=51,97 кН, в том числе длительная составляющая — 0,3·51,97 = 25,99 кН.

Таким образом, суммарная (максимальная) величина продольной силы в колонне первого этажа (при заданном количестве этажей – 5) будет составлять N = (155,32+178,18)·(5-1)+ +211,37+51,97=1597,34 кН; в том числе длительно действующая N_l=(155,32+111,36)·(5-1)+ +211,37+25,99=1304,08 кН.

Характеристики бетона и арматуры для колонны. Бетон тяжелый класса В30, R_b=17 МПа при =1. Продольная рабочая арматура класса A-III, R_s= 365 МПа.

Расчет прочности сечения колонны выполняем на действие продольной силы со случайным эксцентриситетом, поскольку класс тяж. бетона ниже В40, а l₀ = 3300 мм <20h = 20·300 = 6000 мм.

Принимая предварительно коэффициент φ=0,8, вычисляем требуемую площадь сечения продольной арматуры.

мм².

Принимаем 4Ø20 A-III (As = 1256мм²).

Выполним проверку прочности сечения колонны с учетом площади сечения фактически принятой арматуры.

При N_l/N = 1304,08/1597.34=0,82; l₀/h= 3300/300 = 11 и а' = 40мм < 0,15/h = 45 мм;

= 0,882 и = 0,897.

Так как α 0,3, то ,

Тогда фактическая несущая способность расчетного сечения колонны будет равна N_u= = =0,891(17·300²+365·1256)=1771.7 кН > N = 1597,34 кН, , прочность колонны обеспечена. Так же удовлетворяются требования по минимальному армированию, поскольку

%>0.4

Поперечную арматуру в колонне конструируем в соответствии с требованиями из арматуры класса Вр-I диаметром 5 мм, устанавливаемую с шагом s = 350 мм < 20d =20·20 = 400 мм и менее 500 мм.

Фундамент проектируем под рассчитанную выше колонну сечением 300x300 мм с расчетным усилием в заделке N = 1597.34 кН.

Для определения размеров подошвы фундамента вычислим нормативное усилие от колонны, принимая среднее значение коэффициента надежности по нагрузке 1388,99 кН.

По заданию грунт основания имеет условное расчетное сопро­тивление R₀ = 0,28 МПа, а глубина заложения фундамента равна H_f = 1,5 м.

Фундамент должен проектироваться из тяжелого бетона класса В20 (R_bt = 0,9 МПа при =1) и рабочей арматуры класса A-III (R_s=365 МПа).

Принимая средний вес единицы объема бетона фундамента и грунта на обрезах = 20 кН/м³ = 20·10^-6 Н/мм³, вычислим требуемую площадь подошвы фундамента:

м².

Размер стороны квадратной подошвы фундамента должен быть не менее . Назначаем размер а=2,4 м, при этом давление под подошвой фундамента от расчетной нагрузки будет равно р 0,277 МПа.

Рабочую высоту фундамента определяем по условию прочности на продавливание:

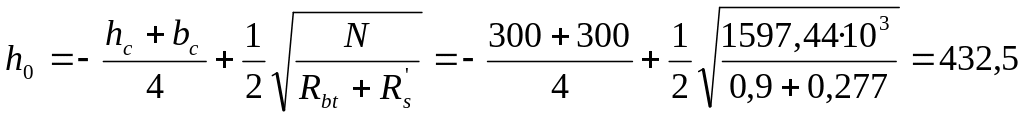мм,

т.е. H=h₀+a=432?5+50= 482?5 мм.

По условию заделки колонны в фундаменте полная высота фундамента должна быть не менее Н = 1,5/h_c +250=700 мм.

По требованию анкеровки сжатой арматуры колонны Ø20 A-III в бетоне класса В30 H= = 19·20+250=630 мм.

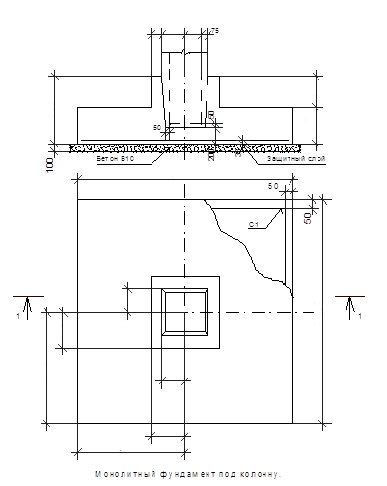
С учетом удовлетворения всех условий принимаем окончатель­но фундамент высотой Н=700 мм, двухступенчатый, с высотой нижней ступени h₁=400 мм. С учетом бетонной подготовки под подошвой фундамента будем иметь рабочую высоту h₀ = Н – а= 700 – 50 = 650 мм и для первой ступени h₀₁ = 400 – 50=350 мм.

Выполним проверку условия прочности нижней ступени фундамента по поперечной силе без поперечного армирования в наклонном сечении, начинающимся в сечении III-III. Для единицы ширины этого сечения ( b = 1 мм)

Q = 0,5(а – h_c – 2h₀)bp =0,5(2400-300-2·650)·1·0,277=110,8 Н.

Поскольку Q =0.6R_btbh₀₁=0.6·0,9·1·350=189 Н > Q = 110,8 Н, то прочность нижней ступени по наклонному сечению обеспечена.

Площадь сечения арматуры подошвы квадратного фундамента определим из условия расчета фундамента на изгиб в сечениях I — I и II — II.

Изгибающие моменты определим:

М_I = 0,125 0,125·0,277(2400 - 300)²·2400 =366,47 кH·м;

M_II = 0,125 0,125·0,277(2400-900)²·2400=186,98 кH·м.

Сечение арматуры одного и другого направления на всю ширину фундамента определим из условий:

= 366,47·10⁶ /(0,9·650·365)=1716 мм² = 17,2 см²;

= 186,98·10⁶/(0,9·350·365) = 16,3 см².

Нестандартную сварную сетку конструируем с одинаковой в обоих направлениях рабочей арматурой 12Ø14 A-III (А_s=1847 мм²), соответственно получим фактическое армирование расчетных сечений =1847·100/(900·650)=0,31%; = =1847·100/(2400·300)=0,26%; что больше %.