Лабораторная работа № 3 вычисление расстояния между кривыми на плоскости

Цель работы: найти расстояние между двумя фигурами на плоскости, используя оптимизационный подход и метод неопределенных множителей Лагранжа. Для компьютерного получения решения и его визуализации использовать пакет MAPLE.

1. Теоретические сведения

1. Метод множителей Лагранжа

Стандартная условно-экстремальная задача формулируется следующим образом:

найти минимум функции (критерия) J = f(x₁, ..., x_n) при наличии ограничений

g₁(x₁, ..., x_n) = 0, …, g_m(x1, ..., x_n) = 0,

или коротко

Основной аналитический метод решения связан с введением вектора множителей Лагранжа и построением составного критерия (функции Лагранжа)

L = f(X) +  g(X)  min

или в более подробной записи

Экстремум этой функции ищется обычным образом путем взятия производных и приравнивания их нулю. Тем самым исходная условно-экстремальная задача сводится к задаче отыскания безусловного экстремума.

Пример 1. Вписанный прямоугольник максимального периметра.

Эллипс задан своим каноническим уравнением Требуется среди всех вписанных в него прямоугольников (рис. 1) найти прямоугольник с максимальным периметром.

y

b

y

x

x

a

2x

2y

Рисунок 1

Решение. Формализуем задачу, выписав критерий и ограничения:

J = 4x + 4y  max; , x, y  0.

Строим составной критерий (функцию Лагранжа):

Приравниваем нулю производные по x и y:

откуда x = 2a² / , y = 2b² / , x /y = a² / b²,

Таким образом, стороны прямоугольника с максимальным периметром относятся как квадраты полуосей эллипса. Подставляя эти значения в уравнение эллипса, находим, что ² = 4а² + 4b². Окончательно имеем

П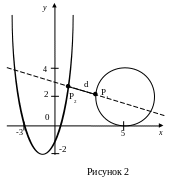 ример 2. Расстояние между окружностью и параболой.

Пусть требуется найти расстояние между окружностью и параболой

Решение. Изобразим окружность и параболу на плоскости (рис. 2). Задача сводится к отысканию точки P₁ с координатами (x₁, y₁), принадлежащей окружности, и точки P₂ с координатами (x₂, y₂), принадлежащей параболе, таких, чтобы расстояние между ними было минимальным. Для облегчения дальнейших вычислений расстояние d можно заменить его квадратом. Выписываем критерий и ограничения:

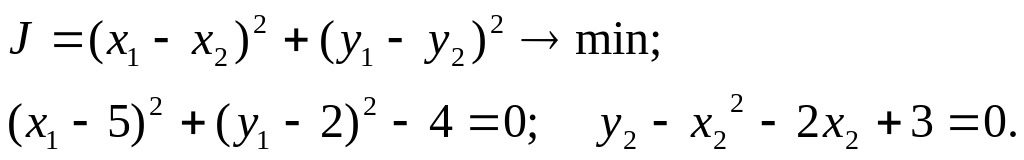
Строим функцию Лагранжа:

Решение задачи теперь сводится к отысканию минимума функции от шести переменных x₁, x₂, y₁, y₂, λ₁, λ₂. Это можно сделать, приравняв соответствующие шесть производных нулю:

Заметим, что два последних уравнения – это просто описание исходных кривых.

Данная ыимееи три различных решения. Геометрически им соответствуют три прямые, показанные на рис. 3. Все они проходят через центр окружности и пересекают одну из ветвей параболы под прямым углом. Заметим, что ортогональность кратчайшего отрезка, соединяющего две кривые, каждой из них – общее свойство задач о минимальном расстоянии.

Отбрасывая лишние решения, находим, что минимальное расстояние между кривыми равно .