1.23. Розподіл Больцмана.

Визначимо густину імовірності того, що одна з частинок системи потрапить в точку , в якій потенціальна енергія цієї частинки дорівнює . При визначенні нас не цікавить, як рухається обрана частинка; не цікавить нас і розташування решти частинок системи.

Всі частинки розглядуваної системи фізично тотожні. Для визначеності, покладемо, що досліджувана частинка має номер 1.

Для визначення шуканої густини імовірності необхідно проінтегрувати по всіх імпульсах і всіх координатах окрім координат першої частинки. В результаті знаходимо, що

, (1.23.1)

де С – нормуюча константа

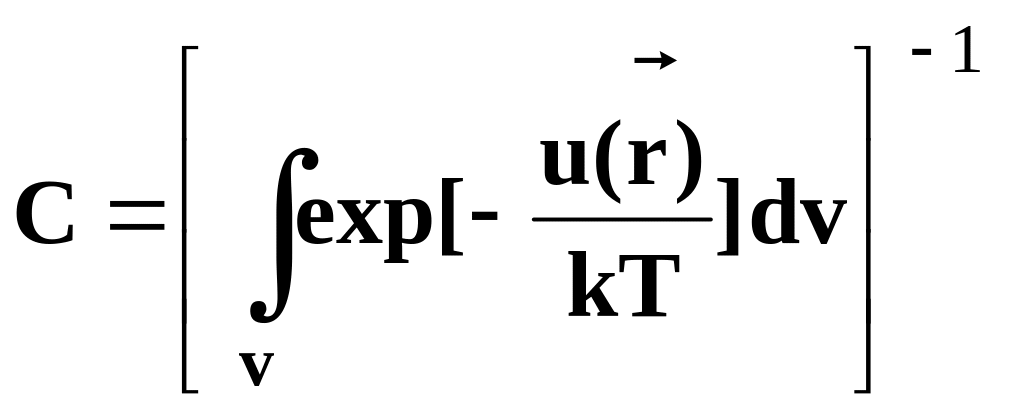. (1.23.2)

Функція має назву функції розподілу Больцмана.

2. Електрика.

2.1. Електричний заряд.

Поняття електричного заряду відноситься до фундаментальних понять фізики. В класичній фізиці заряд може бути визначений, як певна характеристика фізичних тіл, яка зумовлює виникнення між цими тілами специфічної електричної взаємодії. В класичній фізиці електрична взаємодія вважається фундаментальною, тобто такою, яка не може бути інтерпретована, як частковий випадок більш загального типу взаємодій. Фундаментальні закони, які описують електричну взаємодію між зарядженими тілами встановлені експериментально.

Приведемо деякі характерні ознаки електричного заряду:

• заряд є фізичною величиною, яка може бути виміряна; в системі СІ одиницею заряду є кулон (Кл);

• існують заряди двох знаків – додатні і від’ємні (позитивні і негативні);

• величина заряду тіла не залежить від його механічного стану (розташування в просторі, швидкості, прискорення);

• сумарний заряд замкненої системи є константою;

• існує “квант” електричного заряду (елементарний заряд) 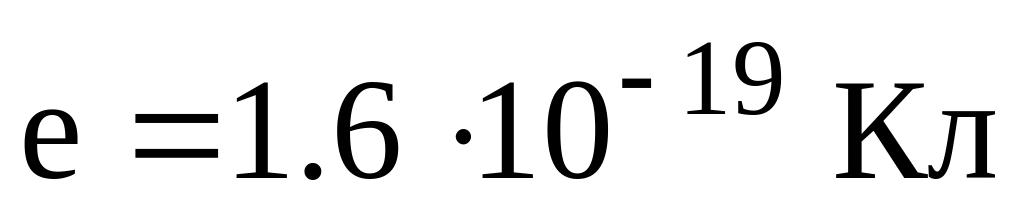, тобто мінімальна кількість заряду, яка може бути передана від одного тіла до іншого. Електричний заряд є невід’ємною характеристикою деяких елементарних частинок: електрон має заряд 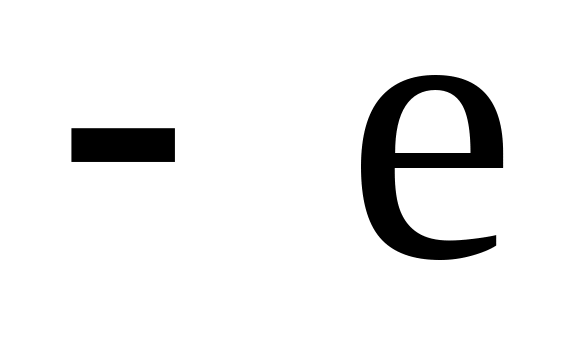, позитрон і протон – заряд .

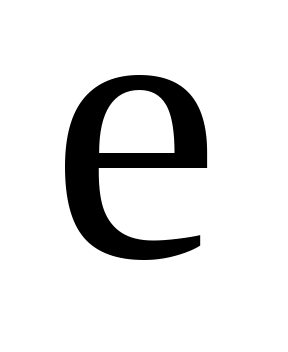Відносно протону, нейтрону і деяких інших “елементарних” частинок слід зробити наступне зауваження. Згідно з сучасним станом теорії елементарних частинок, так звані баріони (до них, зокрема, відносяться протон і нейтрон) насправді не є елементарними, а побудовані з кварків, які можуть мати заряд . Втім кварки як окремі частинки не приймають участі в переносі заряду, і в цьому сенсі заряд дійсно є елементарним.

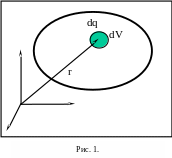
2.2. Густина заряду. Точкові заряди.

Заряд тіла є інтегральною характеристикою тіла: він відноситься до зарядженого тіла як цілого. Виникає природне питання, як саме розподілений заряд в межах зарядженого тіла. Для опису просторового розподілу заряду в об’ємі тіла використовується об’ємна густина заряду , яка визначається наступним чином (рис. 1)

Виділимо в об’ємі тіла елементарний об’єм , розташований в околі точки . Позначимо через заряд, якій знаходиться в об’ємі . Визначимо за допомогою співвідношення

(2.2.1)

Зрозуміло, що

(2.2.2)

На відміну від заряду густина заряду є локальною характеристикою зарядженого тіла і може бути визначеною для будь-якої точки .

Поряд з об’ємною густиною заряду, в електриці визначаються поверхнева густина заряду

(2.2.3)

і лінійна густина заряду

(2.2.4)

Надзвичайно важливу роль в теорії електрики відіграють ідеалізовані об’єкти – точкові заряди (заряджені матеріальні точки). Зрозуміло, що об’ємна густина точкового заряду описується виразом

, (2.2.5)

в якому - тривимірна  - функція Дірака, - точка, в якій розташовано точковий заряд.