1.12. Мікроскопічні параметри системи. Мікростан.

Згідно з молекулярно-кінетичною теорією будови речовини, остання складається з взаємодіючих атомів або молекул. З мікроскопічної точки зору стан такої системи визначається сукупністю параметрів, які, по-перше, описують конфігурацію системи (тобто просторове розташування всіх частинок ), по-друге, характеризують рух всіх частинок в системі. Якщо не брати до уваги “внутрішні” ступені вільності частинок (до яких ми віднесемо і обертальний їх рух), конфігурація системи буде характеризуватись множиною радіусів-векторів, які визначають розташування окремих атомів (молекул), і множиною механічних імпульсів атомів (молекул). Компоненти радіусів-векторів і механічних імпульсів мають назву мікроскопічних параметрів системи, а їх сукупність визначає мікроскопічний стан (або мікростан) системи.

1.13. Конфігураційний, імпульсний і фазовий простори.

Для опису мікростану в системи зручною є побудова багатовимірних конфігураційного, імпульсного і фазового просторів.

Введемо в розгляд вимірний вектор

Вектор є визначеним в вимірному декартовому конфігураційному просторі. Конкретній конфігурації системи відповідає деяка точка в конфігураційному просторі (конфігураційна точка); хронологічна еволюція структури системи еквівалентна переміщенню конфігураційної точки по конфігураційному простору.

вимірний імпульсний простір вводиться аналогічно. Кожна точка цього простору

відповідає конкретному набору механічних імпульсів частинок в системі.

Сукупність конфігураційного і імпульсного простору утворюють фазовий простір .

Вектор

є визначеним в вимірному фазовому просторі. Конкретний мікростан системи характеризується фазовою точкою простору .

Мікростан системи змінюється з часом. Це означає, що , тобто в ході часової (хронологічної) еволюції системи фазова точка рухається в фазовому просторі по фазовій траєкторії. Ця траєкторія може бути замкненою або незамкненою, але не містить перетинів з собою. Для доведення справедливості останнього знайдемо рівняння, що визначають рух фазової точки.

1.14. Рівняння Гамільтона і фазова траєкторія.

В простому випадку, який ми розглядаємо (поступальний рух частинок) механічна енергія системи може бути подана у вигляді

.

Обчислення похідних механічної енергії по і дає наступне

;

.

Два останні рівняння утворюють систему рівнянь Гамільтона.

Сукупність величин визначають швидкість фазової точки . Згідно з рівняннями Гамільтона, швидкість фазової точки визначається тільки її розташуванням . Отже, напрямок вектору , який співпадає з напрямком дотичної до фазової траєкторії, в кожній точці фазового простору визначений однозначно, що виключає можливість перетинання фазової траєкторії з собою.

1.15. Макростани, мікростани і усереднення.

Ми познайомились з двома методами опису стану систем – макроскопічним і мікроскопічним методами і ввели поняття макростану і мікростану. Об’єктами вивчення, до яких застосуються обидва ці методи (незважаючи на їх разючу різницю), є макроскопічні системи, конкретною задачею – опис термодинамічні властивості макроскопічних систем.

В світлі спільності об’єктів і цілей макроскопічного і мікроскопічного методів є зрозумілим, що ці два методи мають бути тісно пов’язаними. Встановленням взаємозв’язку макроскопічного і мікроскопічного методів (отже, макростану і мікростану), а також докладному розгляду мікроскопічного методу опису макроскопічних властивостей об’єктів ми тепер і займемось.

Мікростан системи однозначно визначає її макростан. В той же час кожному макростану відповідає деяка множина мікростанів. Будь-яка макроскопічна фізична величина, яка може бути визначена мікроскопічним методом, обчислюється шляхом усереднення по мікростанах, що можуть реалізовуватись в заданих зовнішніх умовах. Рухаючись по фазовій траєкторії в процесі хронологічної еволюції система послідовно проходить множину мікростанів, по яким проводиться усереднення. Сказане означає, що при такому підході реалізується усереднення по часу, яке прийнято позначати .

В статистичній фізиці безпосереднє усереднення по часу не застосовується. Замість нього використовується усереднення по ансамблю систем . Під ансамблем розуміється множина фізично еквівалентних стаціонарних систем, кожна з яких є “копією” нестаціонарної системи, зробленою в певний момент часу . Отже, замість розгляду руху системи по фазовій траєкторії ми розглядаємо квазіконтинуальну стаціонарну множину фазових точок ансамблю. Очевидно, для довільного має місце

. (1.15.1)

Можливість використання ансамблю систем для усереднення базується на ергодичній гіпотезі, згідно з якою усереднення по часу є еквівалентним усередненню по ансамблю

. (1.15.2

1.16. Функція розподілу ансамблю систем в фазовому просторі.

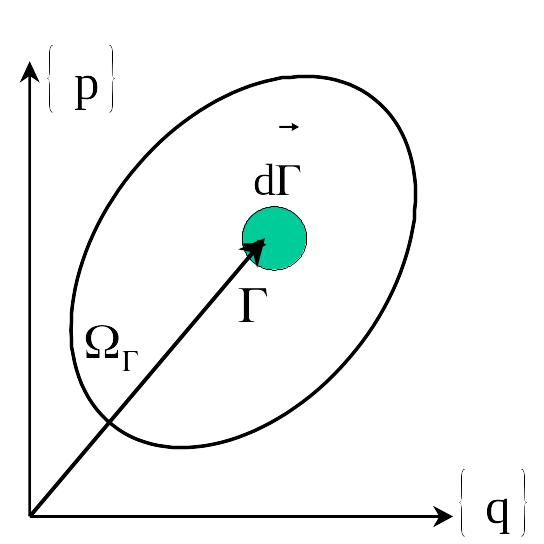Розглянемо в фазовому просторі область , в якій містяться всі фазові точки систем ансамблю. Побудуємо в околі елементарний об’єм (див. рисунок).

Визначимо імовірність того, що будь-яка з належить за допомогою співвідношення

, (1.16.1)

в якому - густина імовірності. В теоретичній фізиці традиційно називають функцією розподілу (не плутати з визначенням функції розподілу, прийнятим в теорії імовірності!).

Функція розподілу є нормованою:

. (1.16.2)

Припустимо, що деяка фізична величина залежить від мікростану системи: . Заданому макростану відповідає усереднене по ансамблю значення цієї величини

. (1.16.3)

Характерним прикладом застосування рівняння (1.16.3) є співвідношення

, (1.16.4)

в якому, як і раніше, - внутрішня енергія, - функція Гамільтона.

Конструкція залежності визначається фізичним змістом величини . Отже, обчислення усереднення типу (1.16.3) буде можливим, якщо відомою є функція розподілу ансамблю в фазовому просторі. Відшукання виду функції розподілу є однією з центральних задач статистичної фізики.

Перш ніж перейти до побудови функції розподілу ансамблю в фазовому просторі, зробимо дуже суттєве зауваження.

В курсі квантової механіки строго доводиться наступна теорема. Нехай є імовірністю прямого переходу системи з стану “К” з енергію в стан “М” з енергією (за одиницю часу), а є імовірністю зворотного переходу між цими станами. Тоді, якщо , має місце , тобто, імовірності прямого і зворотного переходів є рівними.

Неважко збагнути, що наслідком цієї теореми і умови стаціонарності функції розподілу є специфічність залежності функції розподілу від мікростану , яка полягає в тому, що функція розподілу залежить від мікростану не безпосередньо, а через енергію мікростану :

(1.16.5.)