2.38. Електромагнітна індукція.

Розглянемо утворений провідниками прямокутний замкнений контур Г: “12341”, який лежить в площині XY (рис. 28). Ділянки контуру “12”, “34” і “41” нерухомі; ділянка “23” рухається з постійною швидкістю , паралельною осі Y. Контур вміщений в однорідне магнітне поле з індукцією , паралельною осі Z.

Майже вільні заряди (носії струму) в провіднику “23” відносно провідника рухаються хаотично. Однак, враховуючи ту обставину, що провідник “23” є рухомим і переміщується с постійною швидкістю , цю швидкість можна інтерпретувати як швидкість дрейфу носіїв струму.

Сила Лоренца (в вузькому розумінні), яка діє на окремий носій струму дорівнює

(2.38.1)

Усереднена по всіх носіях струму на ділянці “23” сила Лоренца дорівнює

(2.38.2)

Введемо напруженість поля Лоренца

(2.38.3)

Поле Лоренца є типовим полем “сторонніх сил”. За означенням, електрорушійною силою поля Лоренца є інтеграл

, (2.38.4)

де - довжина ділянки “23” контуру. Легко зрозуміти, що добуток швидкості дрейфу на довжину ділянки “23” є просто швидкістю зміни площі , обмеженою контуром

. (2.38.5)

Тепер рівняння (2.38.4) можна записати у вигляді

. (2.38.6)

Вираз в дужках в правій частині рівняння (2.38.6) є магнітним потоком через поверхню ; отже

. (2.38.7)

Ми отримали результат (2.38.7) в припущенні стаціонарності і однорідності магнітного поля; зміна з часом магнітного потоку була зумовлена зміною геометрії контуру інтегрування.

Припустимо, що форма контуру інтегрування є фіксованою, а магнітний потік змінюється за рахунок зміни з часом індукції магнітного поля, тобто . Виявляється, що і в цьому випадку електрорушійна сила індукції описується рівнянням (2.38.7).

Знайдемо диференціальний аналог рівняння (2.38.7) при умові стаціонарності форми контуру інтегрування . З (2.38.7) і (2.38.4), після природного узагальнення, маємо

. (2.38.8)

Використання теореми Стокса дає можливість записати (2.38.8) у вигляді

. (2.38.9)

В просторі, де розташований контур інтегрування, може існувати також електростатичне поле , яке є потенціальним. Повне поле , за принципом суперпозиції, дорівнює

. (2.38.10)

Обчислимо ротор .

. (2.38.11)

Перший доданок в правій частині (2.38.11) дорівнює нулю внаслідок потенціальності електростатичного поля, другій доданок визначається рівнянням (2.38.9). Таким чином, для повного електричного поля маємо

. (2.38.12)

2.39. Струм зміщення. Густина струму зміщення.

В розділі 36 ми отримали рівняння, яке описує циркуляцію вектору напруженості магнітного поля по замкненому контуру

. (2.39.1)

Рівняння (2.39.1) є аналогом теореми про циркуляцію вектора магнітної індукції

. (2.39.2)

Рівняння (2.39.1) і (2.39.2) є точними в тому (і тільки тому!) випадку, коли скрізь в об’ємі системи

, (2.39.3)

тобто макроскопічні струми в системі є постійними.

При обговоренні рівняння (2.39.2) ми відзначали, що шляхом відповідних корекцій його форми це рівняння може бути суттєво вдосконалене, після чого його застосовність розповсюдиться і на змінні струми. Якими мають бути ці корекції ми побачимо нижче.

На рис. 29 зображено електричну схему, яка складається з двох провідників і плоского конденсатору. Будемо заряджати конденсатор струмом ; при цьому на обкладинках конденсатора виникнуть заряди з відповідними поверхневими густинами

(2.39.4)

де С – ємність плоского конденсатору, - площа обкладинки.

Охопимо один з провідників замкненим контуром і спробуємо обчислити інтеграл за формулою (2.39.1); для цього нам необхідно побудувати поверхню інтегрування, “стягнуту” контуром .

Ми побудуємо дві такі поверхні. Перша з них є просто частина площини , обмежена контуром Друга поверхня складається з бічної циліндра і основи , яка знаходиться між обкладинками конденсатора.

Струм перетинає поверхню , тому з рівняння (2.39.1) знаходимо, що циркуляція вектору напруженості магнітного поля по контуру дорівнює струму І. В той же час другу з побудованих поверхонь (вона, нагадаємо, складається з бічної поверхні циліндру і основи ) струм не перетинає, що дає для циркуляції нульове значення.

Зрозуміло, що циркуляція вектору напруженості по замкненому контуру не може залежати від обраної поверхні інтегрування в правій частині рівняння (2.39.1), і отримана нами розбіжність результатів для циркуляції при використанні першої і другої поверхонь інтегрування є незаперечним свідченням некоректності використання (2.39.1) в розглядуваній задачі.

При зарядженні конденсатора в просторі між обкладинками (і тільки там!) виникає однорідне електричне поле. Вектор електричної індукції цього поля чисельно дорівнює , а за напрямком співпадає з зовнішньою нормаллю до площини . Отже, для потоку вектору електричної індукції через поверхню знаходимо

. (2.39.5)

Диференціювання (2.39.5) по часу дає наступне

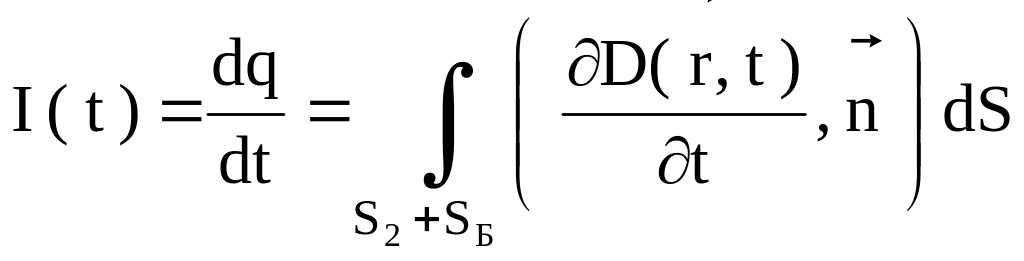. (2.39.6)

Ми довели, що електричний струм, яким заряджується конденсатор, дорівнює потоку похідної по часу вектору електричного зміщення через поверхню, що охоплює одну із обкладинок конденсатора і “стягнена” контуром .

Назвемо цей потік струмом електричного зміщення

, (2.39.7)

а величину

(2.39.8)

• густиною струму зміщення.

Тепер ми можемо внести необхідні корективи в рівняння (2.39.1)

, (2.39.9)

після чого воно стає інваріантним щодо вибору поверхні інтегрування в правій частині.

Диференціальним аналогом рівняння (2.39.9) слугує співвідношення

. (2.39.10)

В провідниках домінуючим доданком є густина звичайного струму , в вакуумі чи непровідних середовищах, навпаки, головну роль відіграє густина струму зміщення.