2.21. Конденсатори. Ємність конденсатора. Енергія зарядженого конденсатора.

В попередньому розділі ми розглянули електричну ємність так званого “усамітненого” провідника; це означає, що інші провідники, які є в системі, знаходяться від “усамітненого” провідника на дуже великих (в ідеалі, нескінчених) відстанях.

“Усамітнені” провідники не є ефективними в плані накопичення зарядів – надто малою виявляється їх електрична ємність. Для прикладу приведемо величину електричної ємності Землі: , і це при таких колосальних розмірах.

Системи провідників спеціальної конфігурації, які призначені ефективно накопичувати заряди, мають назву конденсаторів.

Фізичні причини, з яких саме системи провідників є ефективними накопичувачами зарядів, полягають у наступному. Розглянемо замкнену систему з двох провідників, які в початковому стані є незарядженими і знаходяться на великій відстані один від одного.

Зарядимо провідники: перший – зарядом , другий – зарядом (для замкненої системи заряд провідників є власне перенос заряду з одного провідника до іншого). При цьому між провідниками виникне сила взаємодії , яка, з огляду на протилежність знаків зарядів і , буде силою притягання.

Почнемо повільне зближення провідників. Робота сил притягання для кожного з провідників буде додатною. Отже, зміна потенціальної енергії системи

(2.21.1)

виявляється від’ємною. Це означає, що при зближенні провідників відношення зростає, отже, зростає і електрична ємність системи.

Використання потенціальної енергії системи провідників є коректним, але не дуже зручним. Доцільно було б визначити електричну ємність за рівнянням типу (2.20..7). Складність, яка при цьому виникає, пов’язана з неможливістю визначення потенціалу для системи зарядів.

Виявляється, і це можна довести, виходячи з визначення величини , що для системи двох зарядів електрична ємність визначається рівнянням

, (2.21.2)

де - різниця потенціалів між провідниками.

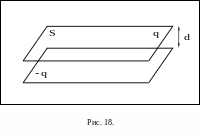Обчислимо електричну ємність плоского конденсатора (рис. 18). Плоский конденсатор складається з двох провідників (обкладинок), що мають форму площин. Площа кожної з цих площин дорівнює , а відстань між площинами дорівнює .

Якщо відстань між площинами набагато менша за лінійні розміри площин, при обчисленні напруженості електростатичного поля між обкладинками площини можна вважати нескінченними (виключенням є вузькі області, що безпосередньо межують з границями пластин).

Заряди і розподілені по площинах рівномірно з поверхневими густинами . За теоремою Гауса, електростатичне поле в об’ємі між пластинами є однорідним; його напруженість перпендикулярна до площин, направлена від додатньо зарядженої пластини до від’ємно зарядженої пластини. За модулем вектор напруженості між обкладинками дорівнює

. (2.21.3)

Оскільки електростатичне поле є однорідним, різниця потенціалів між обкладинками дорівнює

. (2.21.4)

Тепер, згідно з рівнянням (2.21.2), знаходимо для електричної ємності плоского конденсатора

. (2.21.5)

Якщо об’єм між обкладинками заповнений діелектриком з діелектричною проникливістю , формула (2.21.5) набуває вигляду

(2.21.6)

Для циліндричного і сферичного конденсаторів формули для електричної ємності мають наступний вигляд

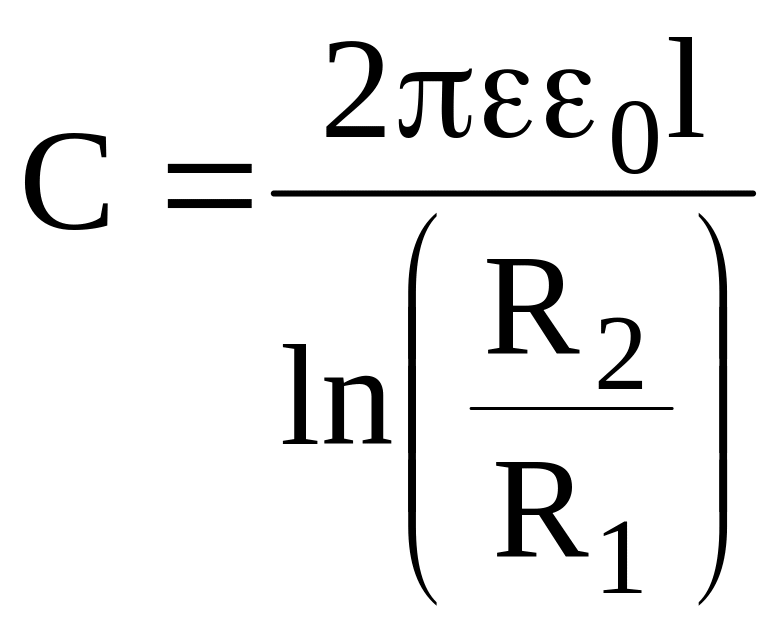(2.21.7)

і

(2.21.8)

Пересвідчитись в справедливості формул (2.21.7) і (2.21.8) пропонується самостійно.

Енергію зарядженого конденсатора отримуємо безпосередньо з формули (2.19.7)

(2.21.9)

Часто величину позначають, як (електрична напруга). При цьому формула (2.21.9) набуває більш звичного вигляду

(2.21.10)

З (2.21.10) легко отримати альтернативні вирази

(2.21.11)