2.17. Причини пропорційності векторів і .
В ізотропному діелектрику дипольний момент є пропорційним до вектору напруженості електричного поля ; за напрямками ці вектори співпадають. Така специфічна і, наголосимо, універсальна поведінка вектору згадувалася вище і використовувалась в попередньому розділі. З огляду на різноманітність внутрішньої будови діелектриків універсальність зв’язку і виглядає дещо дивною і потребує пояснень.
Вектор
поляризації формується з дипольних
моментів окремих молекул. В залежності
від того, яким є дипольний момент
молекули у відсутності зовнішнього
електричного поля, молекули підрозділяються
на неполярні
молекули
і полярні
молекули
.
Відповідно діелектрик, побудований з
неполярних молекул має назву неполярного
діелектрику,
а діелектрик, до складу якого входять
полярні молекули – полярного
діелектрику.
Процеси,
які відбуваються в неполярній молекулі
при “ввімкненні” електричного поля
ілюструються рис. 14 а, б. У відсутності
електричного поля (рис. 14 а) заряди в
молекулі розташовані так, що електричні
центри
співпадають в просторі, і дипольний
момент молекули дорівнює нулю.
Ввімкнемо електричне поле . В результаті додатні заряди дещо змістяться в просторі в напрямку поля, від’ємні – протилежно полю (рис 14 б). Як наслідок, виникне
(2.17.1)
В
слабких (в порівнянні з молекулярними)
полях має місце
і
. (2.17.2)
Отже, в електричному полі неполярна молекула набуває дипольного моменту
. (2.17.3)
Диполі, що задовольняють умовам (2.17.2) і (2.17.3) мають назву пружних диполів.
Якщо
чисельна густина молекул відома і
дорівнює
,
для вектору поляризації неполярного
діелектрика знаходимо (виходячи з
визначення (2.14.1))
(2.17.4)
Для
полярних діелектриків ситуація з
формуванням вектора поляризації є більш
складною. У відсутності поля всі дипольні
моменти молекул мають однаковий модуль
,
але за напрямками орієнтовані хаотично.
При вмиканні електричного поля воно здійснює певну орієнтацію молекулярних диполів “переважно вздовж поля”.
Скористаємося
сферичною системою координат, в якій
.
Зорієнтуємо вісь
вздовж поля
.
Потенціальна енергія диполя
;
отже, орієнтуюча дія електричного поля
вплине на функцію розподілу диполів по
куту
,
а розподіл по куту
залишиться хаотичним. Це призведе до
повної компенсації компонент векторів
,
перпендикулярних полю. З огляду на
сказане вище ясно, що
. (2.17.5)
Для обчислення суми в (2.17.5) скористаємося методами статистичної фізики. Нехай чисельна густина молекул (диполів) дорівнює . Тоді для суми в (2.17.5) маємо
. (2.17.6)
У
випадку слабкого поля
експоненти в інтегралах можна розкласти
в ряд, обмежуючись доданками першого
порядку
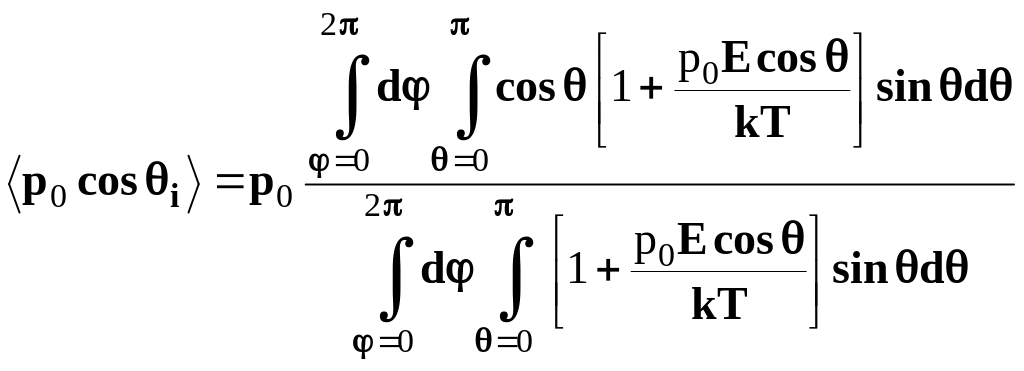, (2.17.7)
звідки, після обчислення інтегралів, знаходимо
. (2.17.8)
Тепер вираз для вектора поляризації (2.17.5) набуває простого вигляду
(2.17.9)
Отже, для полярних діелектриків також має місце пряма пропорційність вектора поляризації і напруженості електричного поля.