2.15. Однорідна поляризація. Поверхнева густина зв’язаного заряду.

Якщо діелектрик поляризований так, що вектор поляризації в діелектрику постійний (тобто не залежить від координат), така поляризація має назву однорідної поляризації.

З рівняння (2.14.13) випливає, що в середині однорідно поляризованого діелектрику об’ємна густина зв’язаного заряду дорівнює нулю. В цьому випадку поляризаційні заряди виникають на поверхні діелектрика і створюють поверхневу густину зв’язаного заряду . Поверхнева густина зв’язаного заряду визначається простим рівнянням

, (2.15.1)

пересвідчитись в справедливості якого пропонується самостійно.

2.16. Вектор електричного зміщення.

Ми з’ясували, що в поляризованому діелектрику виникають зв’язані заряди; в ньому можуть бути присутніми також сторонні заряди. Сумарна густина заряду, отже, визначається виразом

. (2.16.1)

Згідно з теоремою Гауса в диференціальній формі

(2.16.2)

Корисність формули (15.3) для обчислення поля в діелектрику є низькою внаслідок однієї її неприємної особливості. Ця особливість полягає в тому, що в (15.3) напруженість поля визначається зокрема густиною зв’язаного заряду, яка сама залежить від . Задачі такого типу зустрічаються в фізиці досить часто і мають назву самоузгоджених.

Перетворимо рівняння (2.16.2), враховуючи зв’язок (2.14.13)

. (2.16.3)

Введемо в розгляд вектор електричного зміщення

. (2.16.4)

Тепер рівняння (2.16.3) можна подати у вигляді

, (2.16.5)

або, в інтегральній формі

(2.16.6)

Вирази (2.16.5) і (2.16.6) є математичним записом теореми Гауса для вектору електричного зміщення в диференціальній і інтегральній формах, відповідно.

Вектор електричного зміщення є, безумовно, зручною, але дещо штучно введеною величиною. Він не є силовою характеристикою електричного поля і, отже, не визначає дію електричного поля на заряди. Тому введення вектору буде корисним з точки зору опису електричного поля в діелектрику тільки в тому випадку, якщо між векторами і буде встановлено зв’язок.

Такий зв’язок дійсно існує. З причин, які ми обговоримо нижче, має місце

, (2.16.7)

де - діелектрична сприйнятливість. Введемо діелектричну проникливість , після чого з рівнянь (2.16.4) і (2.16.7) безпосередньо отримуємо

. (2.16.8)

Сукупність рівнянь (2.16.5) і (2.16.8) іноді сприймається, як достатня для розрахунку електричного поля в речовині по відомій густині сторонніх зарядів система рівнянь. Насправді таке сприйняття є ілюзорним, і ось чому.

При обчислені електричного поля по відомій густині повного заряду фактично використовувалися два диференціальні рівняння

(2.16.9)

Аналогом першого з рівнянь (2.16.9) є рівняння (2.16.5). Що ж стосується другого з рівнянь (2.16.9), то його аналогу для вектора в загальному випадку просто не існує – векторне поле не обов’язково є потенціальним. Дійсно,

. (2.16.10)

Отже, в двох випадках.

1. В тривіальній, а тому і нецікавій ситуації .

2. У випадку, коли діелектрик є однорідним і ізотропним, тобто . .

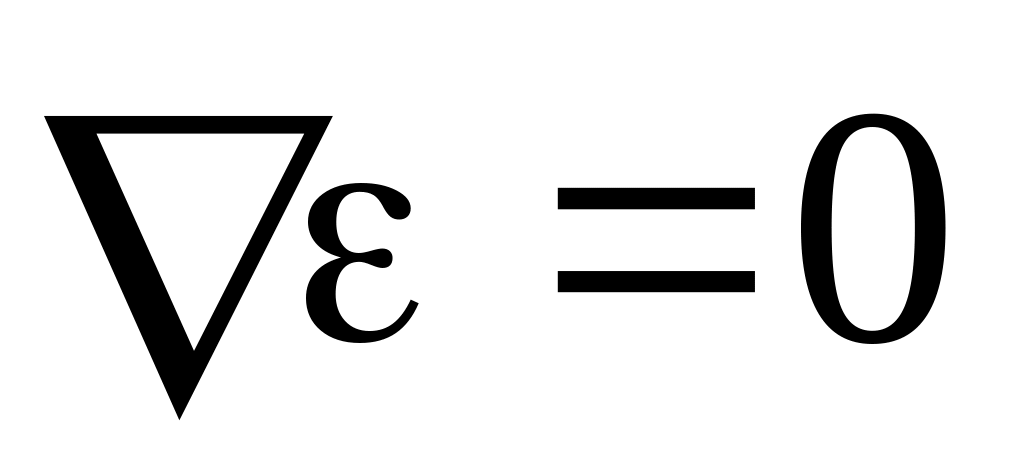Отже, для однорідного і ізотропного діелектрика рівняння (2.16.5) дає можливість обчислити векторне поле , виходячи з відомого розподілу сторонніх зарядів . Це поле на буде залежати від діелектричних властивостей середовища, оскільки зв’язані заряди на нього не впливають.

Обчислимо векторне поле , створене відомим розподілом сторонніх зарядів. З рівняння (2.16.8) маємо для електричного поля в вакуумі

(2.16.11)

Заповнимо простір однорідним ізотропним діелектриком. Векторне поле при цьому не зміниться, а електричне поле в діелектрику стане рівним

. (2.16.12)

Наслідком рівнянь (2.16.11) і (2.16.12) є наступний результат

(2.16.13)