2.13. Стороні і зв’язані заряди в діелектриках.

Розглянемо систему, що містить як частину діелектрик. Електричні заряди, які є в цій системи, можна розділити на дві групи:

1. зв’язані заряди, тобто заряди, які належать до атомів або молекул, з яких побудований діелектрик;

2. стороні заряди, які не входять до складу діелектрика як речовини (хоча геометрично вони можуть знаходитись на поверхні і навіть в об’ємі діелектрику).

Густину сторонніх зарядів позначимо через , густину зв’язаних зарядів – через (тут і далі мається на увазі, що відповідає макроскопічному полю). Отже, повна густина заряду в системі є сумою і .

2.14. Вектор поляризації. Його зв’язок з густиною .

Ми вже відзначали, що ФНМО містить велику кількість молекул. Нехай молекула з номером має дипольний момент . Визначимо вектор поляризації за допомогою рівняння

. (2.14.1)

Якщо макроскопічне електричне поле в речовині відсутнє, вектор поляризації дорівнює нулю. Аналіз визначення (2.14.1) показує, що рівність нулю вектора поляризації може спостерігатись в двох випадках:

1. коли елементарні диполі в ФНМО відсутні, тобто для всіх молекул в ФНМО ;

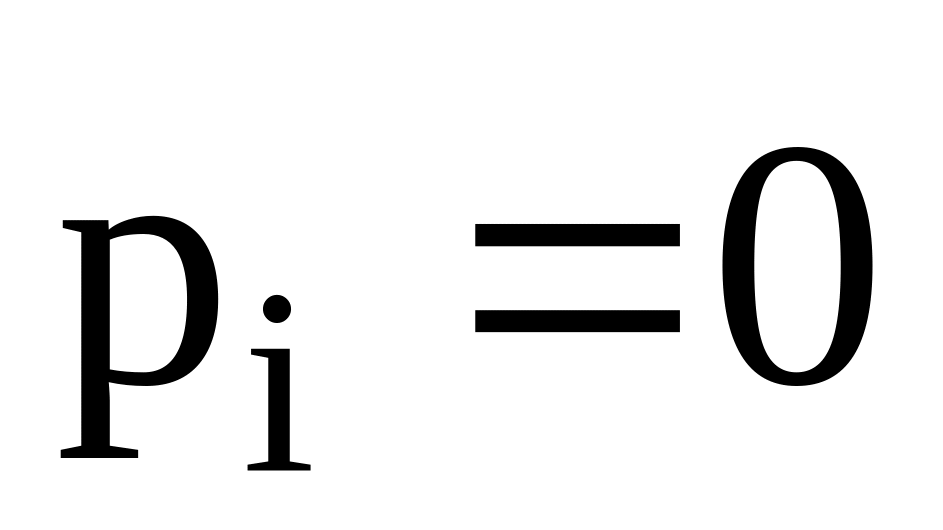2. коли елементарні диполі в ФНМО існують, але орієнтовані повністю хаотично.

Припустимо, що в речовині створене електричне поле . Це поле буде діяти на зв’язані заряди в діелектрику, викликаючи малі (в порівнянні з розмірами ФНМО) їх зміщення. Для випадку 1, описаного вище, таке зміщення призведе до створення елементарних диполів в ФНМО, в другому випадку – до певної орієнтації існуючих в ФНМО диполів відносно напрямку поля .

Отже, під дією електричного поля діелектрик набуває ненульового значення вектора поляризації; в електриці цей процес має назву процесу поляризації діелектрика.

Зрозуміло, що процес поляризації діелектрика супроводжується зміною макроскопічної густини зв’язаного заряду. Встановимо зв’язок між вектором поляризації і .

П очнемо з констатації того факту, що у неполяризованому діелектрику . Далі, звернемо увагу на те, що в діелектрику мають бути заряди принаймні двох типів, які мають різні знаки (інакше електрична нейтральність системи була б неможливою!). При створені поля заряди різних знаків будуть зміщуватись в протилежних напрямках: додатні – вздовж поля, від’ємні – в оберненому напрямку.

Розглянемо деяку замкнену область в діелектрику (рис. 13 а) і детально проаналізуємо процеси, які відбуваються в безпосередній близькості від замкненої поверхні , що обмежує область (рис. 13 б) при “вмиканні” електричного поля.

Для спрощення подальшого розгляду припустимо, що в системі існують зв’язані заряди тільки двох типів: додатні заряди і від’ємні заряди . Таке припущення не зменшує загальності результатів, що будуть отримані і робить розгляд більш “прозорим”.

Введемо позначення

. (2.14.2)

Величини і мають назву чисельних густин зв’язаних зарядів першого і другого типів, відповідно. Чисельні густини визначають макроскопічні густини зв’язаних зарядів першого і другого типів

(2.14.3)

У відсутності в діелектрику електричного поля вектор поляризації дорівнює нулю, і має місце локальна електронейтральність речовини

. (2.14.3)

Рівність (2.14.3) означає, що для довільної області в діелектрику (зокрема, в ФНМО) електричні центри додатного і від’ємного зарядів співпадають.

Створимо в діелектрику електричне поле . Під дією цього поля зв’язані заряди в діелектрику почнуть переміщуватися: додатні – в напрямку поля, від’ємні – протилежно полю. Внаслідок цих переміщень електричні центри додатного і від’ємного зарядів теж дещо перемістяться в просторі і вже не будуть співпадати – в розглядуваній області виникне дипольний момент.

Проаналізуємо процес поляризації діелектрика в безпосередній близькості до поверхні , що обмежує область (рис. 13 б). Під дією поля , яке, з огляду на малість площин можна вважати однорідним, додатні заряди змістяться на вектор , від’ємні заряди – на вектор . З огляду на те, що в однорідному полі зміщення всіх зарядів одного типу є однаковим ( для зарядів першого типу і для зарядів другого типу), можна стверджувати що електричний центр додатних зарядів зміститься на вектор , а електричний центр від’ємних зарядів - на вектор .

Обчислимо дипольний момент циліндру з основами і . Оскільки вектор є визначеним, для обчислення необхідно підрахувати суми

, (2.14.4)

де - об’єм визначеного вище циліндра. З суто геометричних міркувань маємо

. (2.14.5)

звідки

, (2.14.6)

або

. (2.14.7)

Тепер дипольний момент циліндру з об’ємом можна (і зручно) подати у вигляді

, (2.14.8)

звідки для вектор поляризації на елементі поверхні отримуємо

. . (2.14.9)

Обчислимо елемент потоку вектора поляризації через елементарну поверхню .

За означенням

, (2.14.10)

звідки, враховуючи (2.14.9), знаходимо

. (2.14.11)

Сума доданків в правій частині є ніщо інше, як зв’язаний заряд , який в процесі поляризації вийшов за межі області через елементарну поверхню . Оскільки в початковому стані діелектрик неполяризований, зв’язаний заряд , для поляризованого діелектрика маємо

, (2.14.12)

або, в диференціальній формі

(2.14.13)