
- •1.2. Функція стану системи.
- •1.3. Процес в термодинаміці. Квазістатичний процес.
- •1.4. Друге начало термодинаміки.
- •1.5. Метод термодинамічних потенціалів.
- •1.6. Внутрішня енергія як термодинамічний потенціал.
- •1.7. Вільна енергія Гельмгольца.
- •1.8. Ентальпія.
- •1.9. Вільна енергія Гіббса.
- •1.10. Заключні зауваження.
- •1.11. Основи статистичної фізики.
- •1.12. Мікроскопічні параметри системи. Мікростан.
- •1.13. Конфігураційний, імпульсний і фазовий простори.
- •1.14. Рівняння Гамільтона і фазова траєкторія.
- •1.17. Канонічний розподіл Гіббса.
- •1.18. Статистичне визначення ентропії. Статистична вага макростану.
- •1.19. Статистичний інтеграл.
- •1.20. Обчислення статистичного інтегралу для ідеального газу.
- •1.21. Обчислення термодинамічних потенціалів методами статистичної фізики.
- •1.22. Розподіл Максвелла.
- •1.23. Розподіл Больцмана.
- •2. Електрика.
- •2.1. Електричний заряд.
- •2.2. Густина заряду. Точкові заряди.
- •2.3. Закон Кулона.
- •2.4. Електростатичне поле. Вектор напруженості. Принцип суперпозиції.
- •2.5. Потік вектору напруженості електростатичного поля. Теорема Гауса.
- •2.6. Потенціальність електростатичного поля. Скалярний потенціал.
- •2.7. Рівняння Пуассона.
- •2.8. Електричний диполь. Електростатичне поле диполя.
- •2.9. Електростатичне поле системи зарядів на великих відстанях. Дипольне наближення.
- •2.10. Електронейтральна система в однорідному електростатичному полі.
- •2.11. Електричне поле в речовині. Діелектрики, напівпровідники, провідники.
- •12. Мікроскопічні і макроскопічні електричні поля в речовині.
- •2.13. Стороні і зв’язані заряди в діелектриках.
- •2.14. Вектор поляризації. Його зв’язок з густиною .
- •2.15. Однорідна поляризація. Поверхнева густина зв’язаного заряду.
- •2.16. Вектор електричного зміщення.
- •2.17. Причини пропорційності векторів і .
- •2.18. Провідники в електростатичному полі. Електростатичне поле заряджених провідників.
- •2.19. Потенціальна енергія системи зарядів.
- •2.20. Потенціал зарядженого провідника. Електрична ємність. Енергія зарядженого провідника.
- •2.21. Конденсатори. Ємність конденсатора. Енергія зарядженого конденсатора.
- •2.22. Енергія електричного поля.
- •2.23. Електричний струм. Сила електричного струму. Вектор густини електричного струму.
- •2.24. Рівняння нерозривності.
- •2.25. Сторонні сили. Поле сторонніх сил. Електрорушійна сила.
- •2.26. Закон Ома.
- •2.27. Магнітне поле. Індукція магнітного поля. Закон Біо-Савара-Лапласа.
- •2.28. Магнітне поле нескінченого лінійного струму.
- •2.29. Теорема про циркуляцію вектора індукції магнітного поля. Стаціонарні поля і струми.
- •2.30. Магнітне поле заряду, що рухається.
- •2.31. Теорема Гауса для магнітного поля.
- •2.32. Закон Ампера. Сила Лоренца.
- •2.33. Контур з струмом в однорідному магнітному полі.
- •2.34. Магнітне поле контуру з струмом.
- •2.35. Намагнічування речовини. Вектор намагніченості.
- •2.36. Напруженість магнітного поля.
- •2.37. Обчислення магнітного поля в магнетиках.
- •2.38. Електромагнітна індукція.
- •2.39. Струм зміщення. Густина струму зміщення.
- •2.40. Явище самоіндукції. Індуктивність.
- •2.41. Фундаментальна система рівнянь Максвелла.
- •2.42. Хвильове рівняння для електромагнітного поля.
- •2.43. Властивості електромагнітних хвиль.
- •3. Оптика.
- •3.1. Предмет оптики. Світло як електромагнітна хвиля.
- •3.2. Когерентні хвилі. Явище інтерференції.
- •3.3. Інтерференція двох циліндричних хвиль. Інтерференційні смуги.
- •3.4. Дифракція світла. Принцип Гюйгенса-Френеля.
2.7. Рівняння Пуассона.
Теорема
Гауса в диференціальній формі (2.5.13) і
рівняння, яке визначає зв’язок
напруженості електростатичного поля
з його потенціалом
![]() (2.6.10) дає можливість знайти диференціальне
рівняння, що пов’язує потенціал
електростатичного поля з просторовим
розподілом заряду в системі. Для
зручності, приведемо повторно рівняння
(2.5.13) і (2.6.10)
(2.6.10) дає можливість знайти диференціальне
рівняння, що пов’язує потенціал
електростатичного поля з просторовим
розподілом заряду в системі. Для
зручності, приведемо повторно рівняння
(2.5.13) і (2.6.10)
![]() (2.7.1)
(2.7.1)
Підстановка виразу (2.7.1 b) в рівняння (2.7.1 а) дає наступне
![]() (2.7.2)
(2.7.2)
Вслід за Хевісайдом, перетворимо ліву частину рівняння (2.7.2), надавши їй типово “операторного” вигляду
![]() (2.7.3)
(2.7.3)
де
![]() (2.7.4)
(2.7.4)
має назву оператору Лапласа.
З урахуванням співвідношення (2.7.3) і визначення (2.7.4), рівняння (2.7.2) набуває кінцевого вигляду
![]() .
(2.7.5)
.
(2.7.5)
Рівняння (2.7.5) має назву рівняння Пуассона і є одним з центральним рівнянь електростатики. Саме рівняння Пуассона дозволяє розв’язати основну пряму задачу електростатики, яка полягає в описі електростатичного поля (в термінах напруженості або потенціалу) системи з відомим просторовим розподілом заряду .
2.8. Електричний диполь. Електростатичне поле диполя.
Е лектричний
диполь – це електронейтральна система
двох зв’язаних точкових зарядів
лектричний
диполь – це електронейтральна система
двох зв’язаних точкових зарядів
![]() .
Взаємне розташування цих зарядів в
просторі характеризується вектором
.
Взаємне розташування цих зарядів в
просторі характеризується вектором
![]() ,
проведеним від від’ємного заряду до
додатного (рис. 9).
,
проведеним від від’ємного заряду до
додатного (рис. 9).
Основною фізичною характеристикою електричного диполя є його дипольний момент
![]() (2.8.1)
(2.8.1)
Якщо модуль вектора є постійним і не залежить від зовнішніх умов (наприклад, від напруженості електричного поля, в яке вміщений диполь), такий диполь має назву жорсткого диполя. В протилежному випадку диполь називають нежорстким; серед нежорстких диполів особливе місце займають так звані пружні диполі.
Розрахувати напруженість електростатичного поля диполя неважко. Дійсно, заряди, що утворюють диполь, є точковими; отже, обчислення парціальних напруженостей полів, які вони створюють, є елементарним. Далі необхідно застосувати принцип суперпозиції, що і призводить до визначення напруженості електростатичного поля диполя в довільній точці простору.
Спеціальний
інтерес представляє поведінка
електростатичного поля диполя на великих
(в порівняння з
![]() відстанях між диполем і точкою
спостереження. Нижче ми отримаємо
відповідні асимптотичні вирази, які
описують напруженість поля і потенціал
диполя на великих відстанях.
відстанях між диполем і точкою
спостереження. Нижче ми отримаємо
відповідні асимптотичні вирази, які
описують напруженість поля і потенціал
диполя на великих відстанях.
П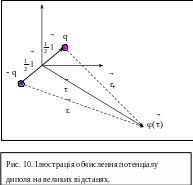 очнемо
з опису асимптотичної поведінки
потенціалу диполя на великих відстанях.
Для зручності розташуємо систему
координат так, щоб її початок співпадав
з серединою вектора
(рис. 10).
очнемо
з опису асимптотичної поведінки
потенціалу диполя на великих відстанях.
Для зручності розташуємо систему
координат так, щоб її початок співпадав
з серединою вектора
(рис. 10).
Введемо позначення:
 -
вектор, проведений з центру диполя в
точку спостереження;
-
вектор, проведений з центру диполя в
точку спостереження;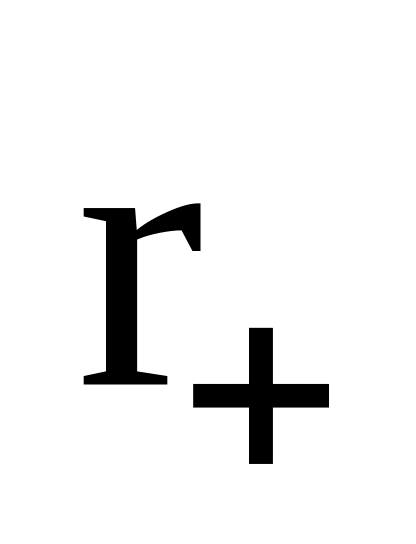 -
вектор, проведений з заряду
в точку спостереження;
-
вектор, проведений з заряду
в точку спостереження; -
вектор, проведений з заряду
-
вектор, проведений з заряду
 в точку спостереження;
в точку спостереження; -
парціальний потенціал, що створюється
зарядом
в точку спостереження;
-
парціальний потенціал, що створюється
зарядом
в точку спостереження;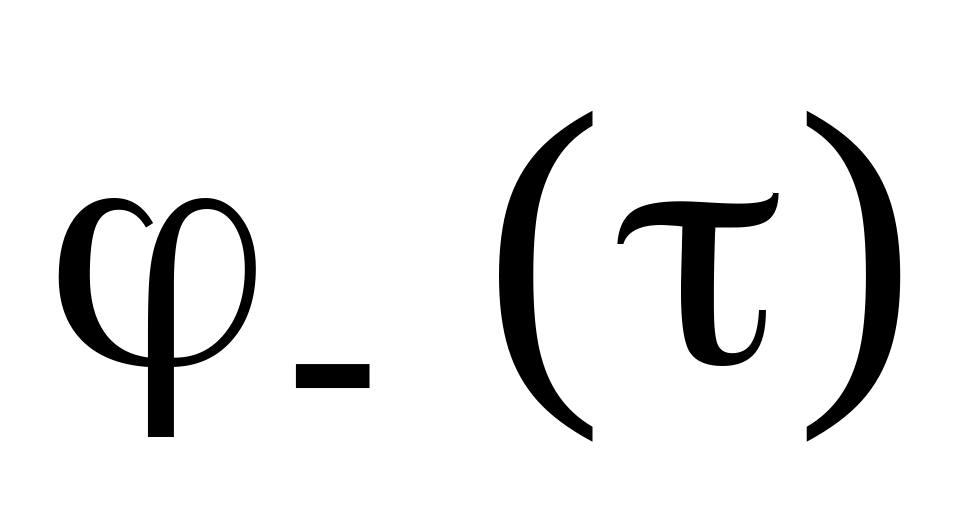 -
парціальний потенціал, що створюється
зарядом -
в точку спостереження.
-
парціальний потенціал, що створюється
зарядом -
в точку спостереження.
Ми досліджуємо поведінку потенціалу диполя на великих відстанях, отже, в наших позначеннях
![]() (2.8.2)
(2.8.2)
Обчислимо
парціальні потенціали
![]() і
і
![]()
![]() (2.8.3)
(2.8.3)
Вектори , і зв’язані співвідношеннями
![]() (2.8.4)
(2.8.4)
Обчислимо модулі векторів і . З виразів (2.3.8) маємо
![]() (2.8.5)
(2.8.5)
Використаємо умову “великих відстаней” (2.8.2), яка дозволяє перейти від точних виразів (2.8.5) до відповідних наближених виразів і, з рештою, знайти достатньо прості і зручні формули, які описують електростатичне поле диполя на великих відстанях.
Звернімо
увагу на наступну суттєву обставину.
Якщо умова (2.8.2) виконується, для доданків,
які знаходяться під знаком “![]() ”
в рівняннях (2.8.5), виникає наступна
ієрархія величин
”
в рівняннях (2.8.5), виникає наступна
ієрархія величин
![]() . (2.8.6)
. (2.8.6)
Це дозволяє записати замість точних співвідношень (2.8.5) відповідні наближені вирази
![]() (2.8.7)
(2.8.7)
Сумісне використання рівнянь (2.8.3), (2.8.7) і принципу суперпозиції для потенціалу дозволяє записати для потенціалу диполя на великих відстанях наступний наближений вираз
![]() (2.8.8)
(2.8.8)
Враховуючи,
що
![]() ,
функції
,
функції
![]() в рівнянні (2.8.8) можна розкласти в ряд
Тейлора в околі точки
в рівнянні (2.8.8) можна розкласти в ряд
Тейлора в околі точки
![]() ,
зберігаючи доданки нульового і першого
порядків. Після відповідних перетворень,
отримуємо
,
зберігаючи доданки нульового і першого
порядків. Після відповідних перетворень,
отримуємо
![]() (2.8.9)
(2.8.9)
Вираз (2.8.9) описує потенціал електростатичного поля диполя на великих відстанях.
Перейдемо до обчислення напруженості електростатичного поля диполя на великих відстанях. Для цього ми використаємо загальний зв’язок між потенціалом і напруженістю електростатичного поля (2.6.10)
![]() . (2.8.10)
. (2.8.10)
В
виразі (2.8.10)
![]() .
Після обчислення градієнтів в рівнянні
(2.8.10) отримуємо для напруженості
електростатичного поля диполя
.
Після обчислення градієнтів в рівнянні
(2.8.10) отримуємо для напруженості
електростатичного поля диполя
![]() (2.8.11)
(2.8.11)
Електростатичне
поле диполя є аксіально симетричним;
вісь симетрії за напрямком співпадає
з вектором
![]() .
Вектори
.
Вектори
![]() лежать в одній площині. Пересвідчитись
в справедливості останнього твердження
пропонується
самостійно.
лежать в одній площині. Пересвідчитись
в справедливості останнього твердження
пропонується
самостійно.
