
- •Контрольная работа «линейная алгебра»
- •Контрольные варианты к задаче 1.
- •Контрольная работа «Векторная алгебра и аналитическая геометрия»
- •Контрольные варианты к задаче 1.
- •Контрольные варианты к задаче 2
- •Контрольные варианты к задаче 3
- •Контрольные варианты к задаче 4
- •Контрольные варианты к задаче 5
- •Контрольные варианты к задаче 6
- •Контрольные варианты к задаче 7
- •Контрольные варианты к задаче 8
- •Контрольная работа «Математический анализ»
- •Контрольные варианты к задаче 1
- •Контрольные варианты к задаче 2
- •Контрольные варианты к задаче 3
Контрольная работа «линейная алгебра»
Вычислить определители
а)

Решение. Этот определитель вычислим по правилу диагоналей. Приписываем справа к определителю первый и второй столбцы. Перемножаем элементы, стоящие на главной диагонали и складываем это произведение с аналогичными произведениями элементов, стоящих на диагоналях, параллельных главной. Затем к произведению элементов, стоящих на побочной диагонали, прибавляем аналогичные произведения элементов, стоящих на диагоналях, параллельных побочной. Затем от первой суммы вычитаем вторую. Это и будет искомый определитель.
7 8 9 7 8 |
|
Ответ:
![]()
Задача
1.
Решить
систему по формулам Крамера:
 .
.
запишем определитель системы

Заменим
в
![]() столбец коэффициентов при
столбец коэффициентов при
![]() на столбец правых частей
на столбец правых частей


 Заменим
в
столбец коэффициентов при
Заменим
в
столбец коэффициентов при
![]() на столбец правых частей
на столбец правых частей



Заменим в
столбец коэффициентов при
![]() на столбец правых частей
на столбец правых частей




 .
.
По
формулам Крамера получаем решение
 .
.
Ответ:
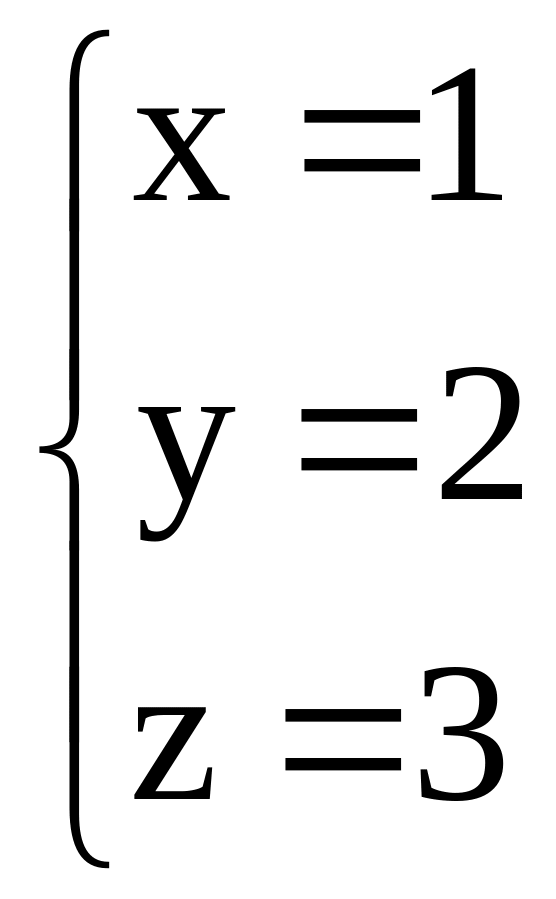 .
.
Контрольные варианты к задаче 1.
Решить системы по формулам Крамера:
1. |
а)
|
б)
|
2. |
а)
|
б)
|
3. |
а)
|
б)
|
4. |
a)
|
б)
|
5. |
а)
|
б)
|
6. |
а)
|
б)
|
7. |
а)
|
б)
|
8. |
а)
|
б)
|
9. |
а)
|
б)
|
10. |
а)
|
б)
|
11. |
а)
|
б)
|
12. |
а)
|
б)
|
13. |
а)
|
б)
|
14. |
а)
|
б)
|
15. |
а)
|
б)
|
16. |
а)
|
б)
|
17. |
а) ; |
б) . |
18. |
а) ; |
б) . |
19. |
а) ; |
б) . |
20. |
a) ; |
б) . |
21. |
а) ; |
б) . |
22. |
а) ; |
б) . |
23. |
а) ; |
б) . |
24. |
а) ; |
б) . |
25. |
а) ; |
б) . |
26. |
а) ; |
б) . |
27. |
а) ; |
б) . |
28. |
а) ; |
б) . |
29. |
а) ; |
б) . |
30. |
а) ; |
б) . |
Контрольная работа «Векторная алгебра и аналитическая геометрия»
Задача
1. Если
известны координаты точек
![]() и
и
![]() ,
то координаты вектора
,
то координаты вектора
![]()
Разложение
этого вектора по ортам
![]() :
:
![]()
Длина
вектора находится по формуле
![]() а направляющие косинусы равны
а направляющие косинусы равны
![]() Орт вектора
Орт вектора
![]()
Пример
1. Даны точки
![]()
Разложить
вектор
![]() по ортам
по ортам
![]() и найти его длину, направляющие косинусы,
орт вектора
и найти его длину, направляющие косинусы,
орт вектора
![]() .
Найдем координаты векторов:
.
Найдем координаты векторов:
![]()
![]()
![]() и
и
![]()
Вектор
![]()
![]()
![]()
![]()
![]()
![]()


 2 3 1
2
2 3 1
2

 ;
;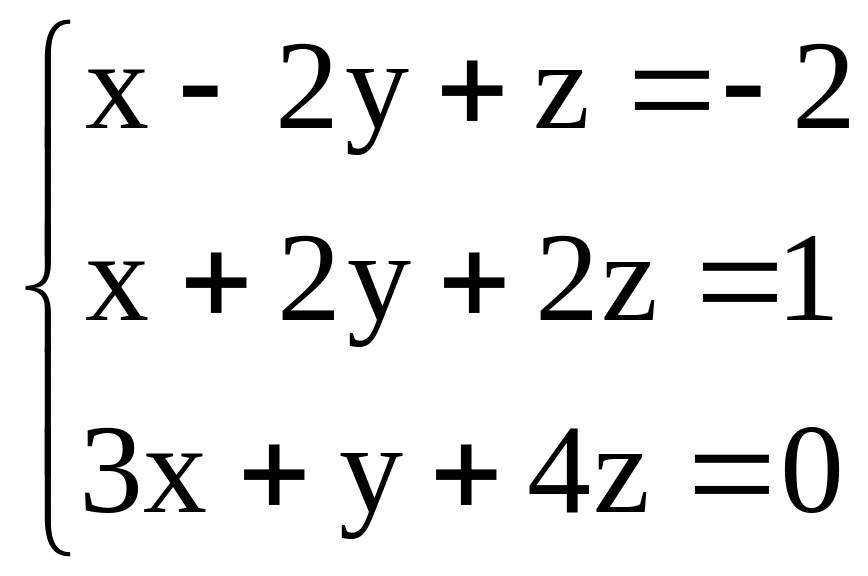 .
. ;
; .
. ;
; .
. ;
; .
. ;
; .
.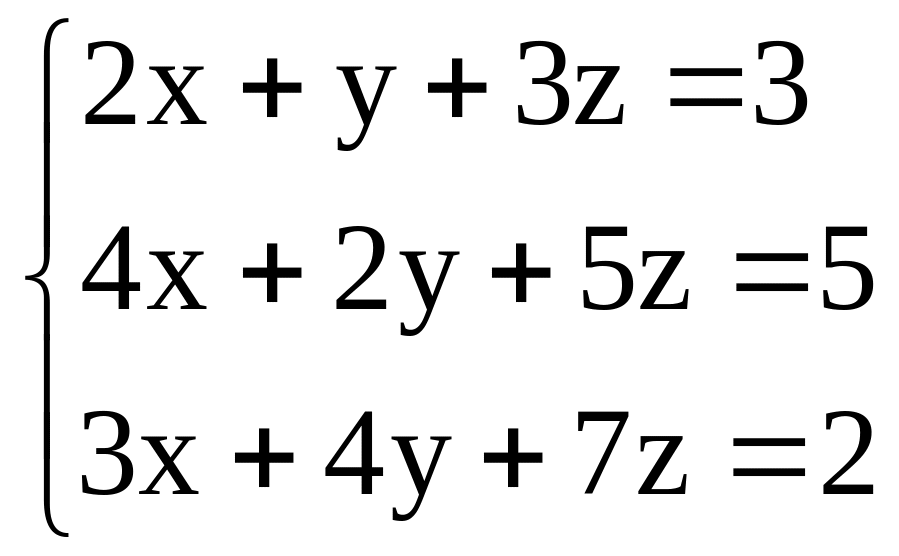 ;
; .
. ;
; .
. ;
; .
.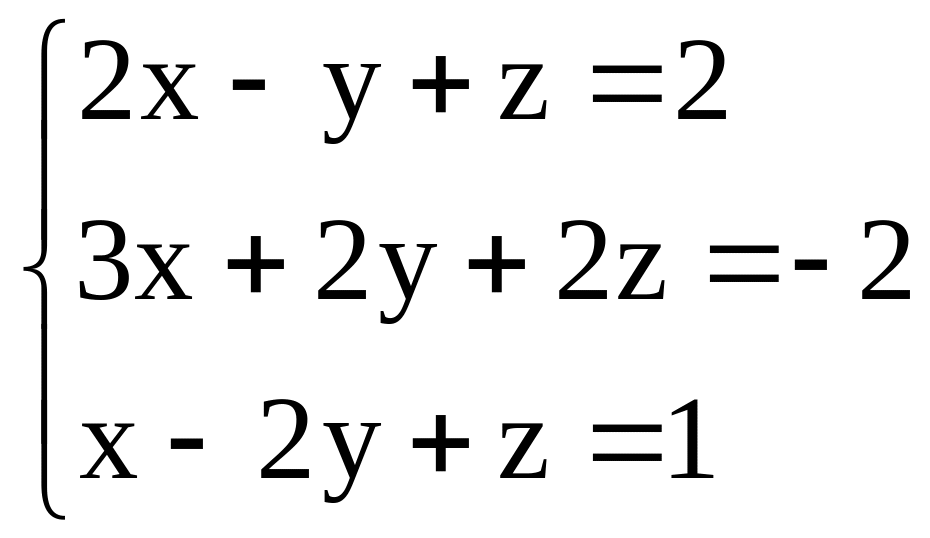 ;
;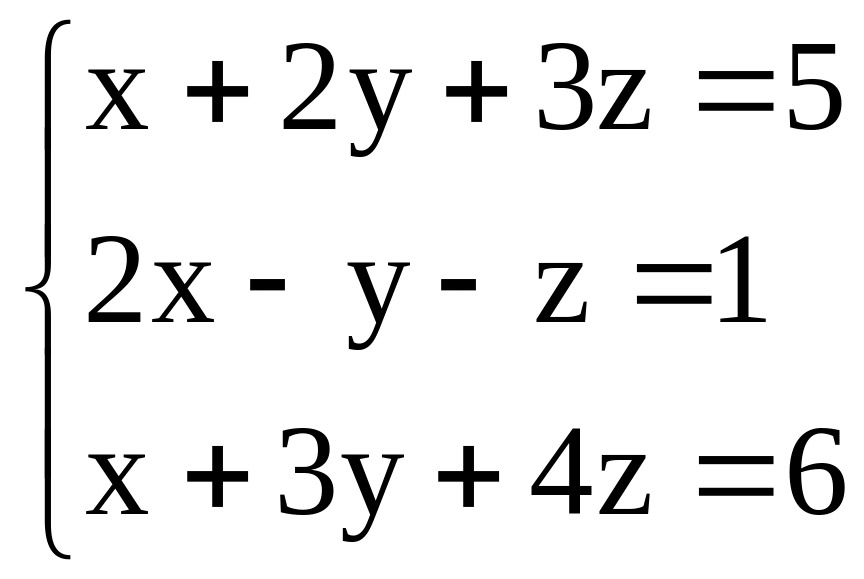 .
.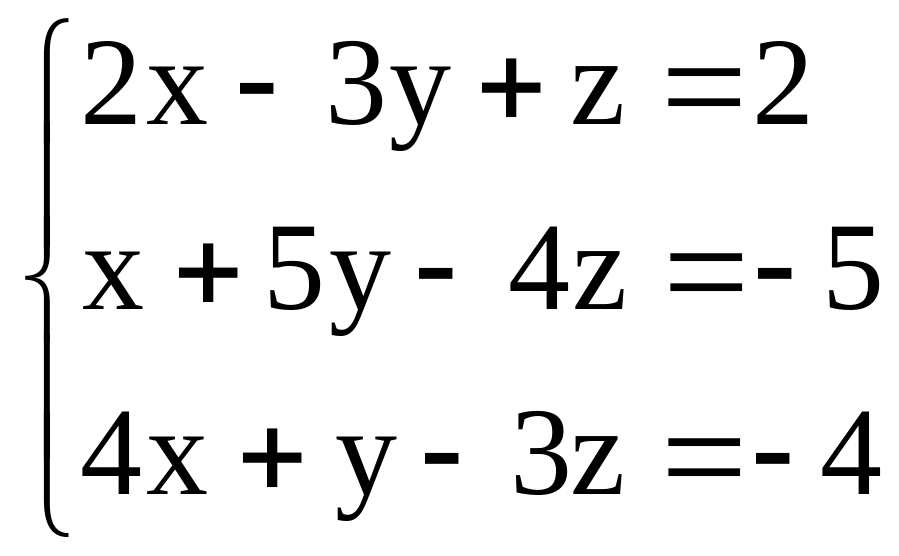 ;
; .
. ;
; .
.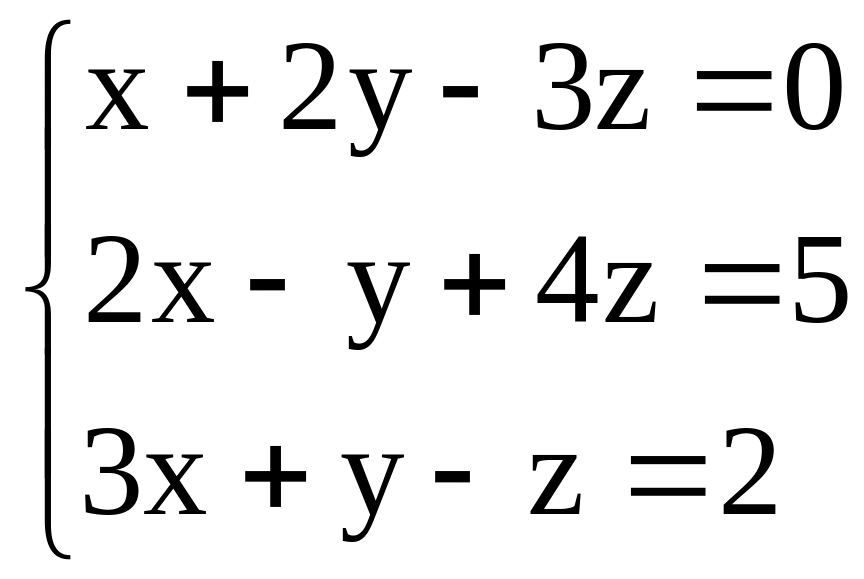 ;
; .
. ;
; .
. ;
; .
. ;
; .
. ;
; .
.