
- •Методические указания
- •Уфа 2000
- •Методические указания
- •А б в
- •Алгебраический критерий устойчивости Гурвица
- •Тогда для устойчивости сау необходимо и достаточно, чтобы все определители имели тот же знак, что и коэффициентb0 . Частотный критерий устойчивости Найквиста
- •Лабораторная работа рс 3
- •Лабораторная работа рс-4
- •Список используемых источников
- •Приложение
Список используемых источников
1.Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. - М. : Наука,1975.
2.Попов Е.П. Теория нелинейных систем автоматического регулирования и управления. – М.: Наука, 1979. 256с.
3. Теория автоматического управления. Часть 2 / Под ред. А.В. Нетушила.
- М.: Высшая школа. 1968.
Приложение
Преобразование модели SIMULINKв модельCONTROLSYSEMMATLAB
Модель в виде структурной схемы в SIMULINKявляется более простым и наглядным представлением системы, чем в виде передаточных функций в тулбоксеCONTROLSYSEM. В тоже время тулбоксCONTROLSYSEMпредставляет широкие возможности по анализу САУ. Поэтому часто возникает задача преобразования структурной схемыSIMULINKв модельCONTROLSYSEM. Рассмотрим алгоритм такого преобразования.
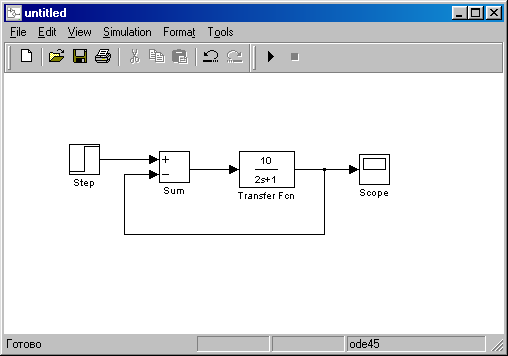 1)Создание структурной схемы в SIMULINK.
Рекомендуется сначала создать схему
для моделирования, затем преобразовать
ее в схему для анализа. Для этого
необходимо отключить задающее
воздействие, к
1)Создание структурной схемы в SIMULINK.
Рекомендуется сначала создать схему
для моделирования, затем преобразовать
ее в схему для анализа. Для этого
необходимо отключить задающее
воздействие, к
 входу
системы подключить входной порт, а
к выходу – выходной порт (блокиIn;Out); разорвать главную
обратную связь при анализе устойчивости
(при анализе динамических звеньев, как
в лабораторной работе РС-1, можно сразу
собрать схему рис. П.2, причем Рис.П.1
Исходная модель без
сумматора).
входу
системы подключить входной порт, а
к выходу – выходной порт (блокиIn;Out); разорвать главную
обратную связь при анализе устойчивости
(при анализе динамических звеньев, как
в лабораторной работе РС-1, можно сразу
собрать схему рис. П.2, причем Рис.П.1
Исходная модель без
сумматора).
Пример исходной и преобразованной системы приведен на рис. П.1, рис. П.2.
2) Извлечение информации из модели:
>> [A,B,C,D]=linmod (‘untitled’)
A=
-0.5000
B=
1
C=
5
D=
Рис. П.2 Преобразованная модель0
С использованием функции linmod получается описание модели в пространстве состояний с помощью матриц состоянияA,B,C,D. В качестве параметра функцииlinmod указывается имя модели (оно указано в заголовке окна модели).
3) Преобразование матриц состояния в модель CONTROLSYSEM:
<< sys =ss(A,B,C,D)
a=
x1
x1 -0.5
b=
u1
x1 1
c=
x1
y1 5
d=
u1
y1 0
Continuous – time mode1.
Параметрами функцииss являются матрицы состояния;sys –имя получаемой модели.
Полученная модель может использоваться для построения временных и частотных характеристик динамических систем и элементов:
- переходная – с помощью функции step:
<< step (sys) ; grid
(grid – отображение сетки графика)
- весовая (импульсная переходная) - с помощью функции impulse:
<< impulse(sys); grid
- логарифмическая амплитудная и фазовая частотные характеристики - с помощью функции bode:
<< bode(sys); grid
При этом диапазон частот выбирается автоматически. Требуемый диапазон частот можно задать
<< bode(sys,(0.01 1000))
амплитудно-фазовая частотная характеристика - с помощью функции nyquis:
<< nyquist(sys); grid или, соответственно,
<< nyquist(sys,(0.01 1000)).
Отметим, что АФЧХ строится как для положительных, так и для отрицательных частот.
