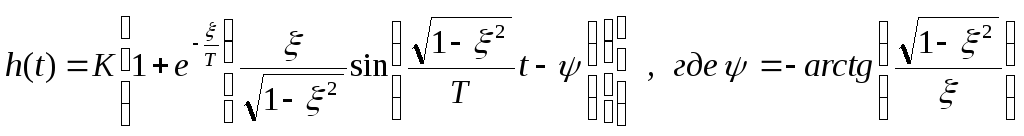Лабораторная работа №1

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФИЛИАЛ В Г. ИШИМБАЙ

Отчет по лабораторной работе №1

по предмету «Теория автоматического управления»

на тему: Исследование характеристик типовых динамических звеньев

Выполнил: студент гр. АТП-308

Шарипов Д.В.

Приняла: Перевертайло Ю.В.

Ишимбай 2006

1. Цель работы

Целью работы является изучение временных и частотных характеристик типовых динамических звеньев с использованием пакета прикладных программ.

2. Основные сведения

Под типовым динамическим звеном понимают устройство любого физического вида и конструктивного оформления, но описываемое дифференциальным уравнением не выше второго порядка.

В таблице (1.1) приведён перечень типовых динамических звеньев и их передаточные функции.

№ п/п	Тип звена	Передаточная функция
1	Безынерционное
2	Апериодическое 1-го порядка
3	Апериодическое 2-го порядка
4	Колебательное
5	Консервативное
6	Идеальное интегрирующее
7	Интегрирующее с замедлением
8	Изодромное
9	Идеальное дифференцирующее
10	Дифференцирующее с замедлением

 

Временные характеристики динамического звена – это его реакция на входные воздействия стандартного вида при определённых начальных условиях.

Переходная функция h(t) звена – это реакция звена (выходной сигнал) на единичное ступенчатое воздействие 1(t) при нулевых начальных условиях.

Частотные характеристики звена определяют его реакцию на гармонический входной сигнал в установившемся режиме.

Частотную передаточную функцию можно определить аналитически следующим образом.

В передаточную функцию разомкнутой системы

подставим и получим частотную передаточную функцию:

где

– амплитудная частотная характеристика;

– фазовая частотная характеристика;

– вещественная и мнимая части частотной передаточной функции.

С целью сокращения объёма вычислительных работ очень часто строят логарифмические частотные характеристики:

1.      Логарифмическая амплитудная частотная характеристика (ЛАХ):

2.    Логарифмическая фазовая частотная характеристика (ЛФХ) - . Эта

характеристика совпадает с нелогарифмической кривой, но строится в

логарифмическом масштабе частоты.

3. Выполнение работы

Интегрирующее звено

Данное звено имеет передаточную функцию:
Переходная функция идеального интегрирующего звена:
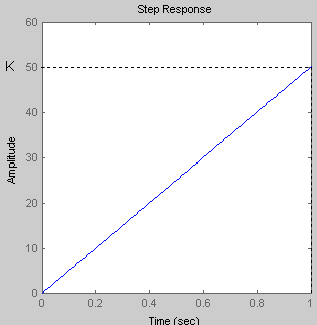
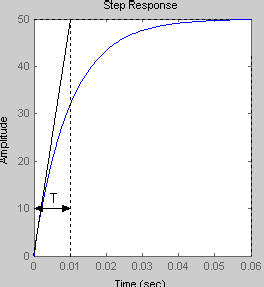
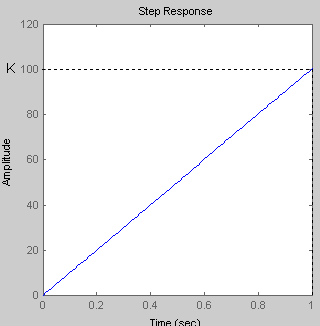
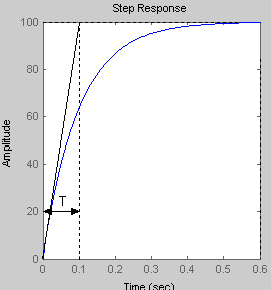
При t=1c h(t) =50	При t=1c h(t) =100

Так как переходная функция идеального интегрирующего звена прямо пропорциональна коэффициенту усиления К, то при его увеличении происходит увеличение выходного сигнала.

Логарифмическая амплитудная и фазовая частотные характеристики:
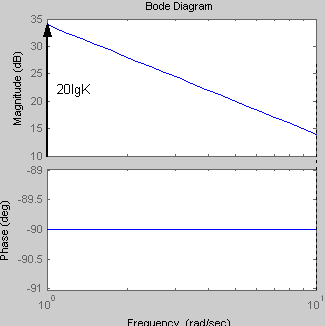
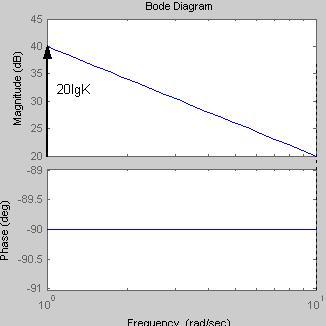
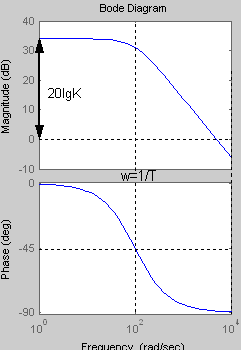
Увеличение коэффициента К интегрирующего звена приводит к увеличению значения амплитуды. Сдвиг по фазе является величиной постоянной равной . Амплитудно-фазовая частотная характеристика имеет вид: W(jω)=

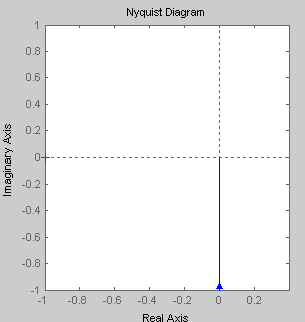
АФЧХ интегрирующего звена представляет собой прямую, совпадающую с мнимой осью, в частности с ее отрицательной частью. Изменение коэффициента К не приводит к каким-либо изменениям.

Апериодическое звено первого порядка

Передаточная функция данного звена имеет вид
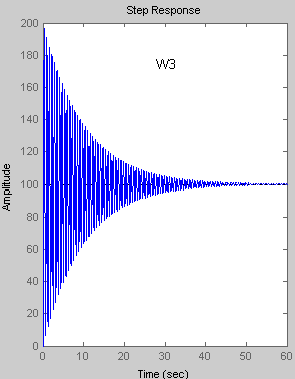
Переходная функция имеет вид
K=hуст	K=hуст		K=hуст
Переходная функция апериодического звена с течением времени стремится к своему установившемуся значению hуст, которое равно коэффициенту усиления K. Поэтому при увеличении коэффициента К увеличивается установившееся значение выходного сигнала. Величина T характеризует степень инерционности динамического звена: увеличение значения постоянной времени T приводит к увеличению времени необходимого для достижения установившегося значения.
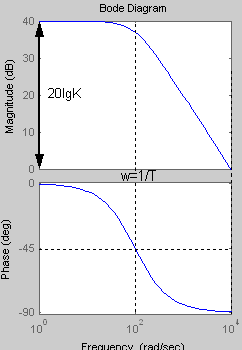
Логарифмическая амплитудная и фазовая частотные характеристики:

При увеличении коэффициента К увеличивается значение амплитуды, на фазу изменение коэффициента К не влияет. Увеличение постоянной времени Т приводит к уменьшению частоты сопряжения.

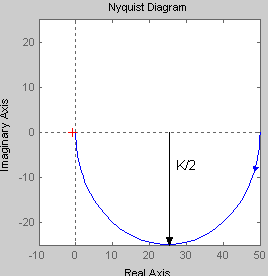
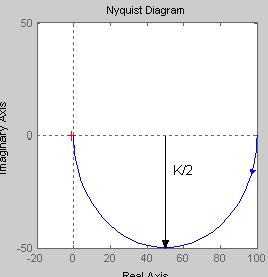
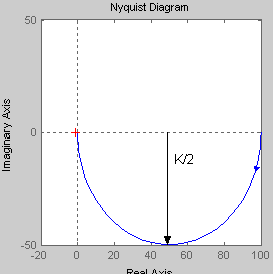
Амплитудно-фазовая частотная характеристика имеет вид:
Графиком АФЧХ апериодического звена является полуокружность с радиусом К/2, центр которой находится на действительной положительной полуоси в точке с координатами (К/2; 0). Таким образом, при увеличении коэффициента К происходит увеличение радиуса полуокружности. Изменение постоянной времени Т не приводит к каким-либо изменениям.

Колебательное звено второго порядка

Передаточная функция имеет вид:
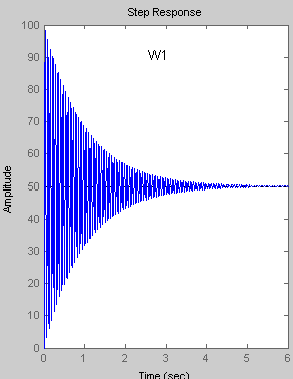
Переходная функция имеет вид:

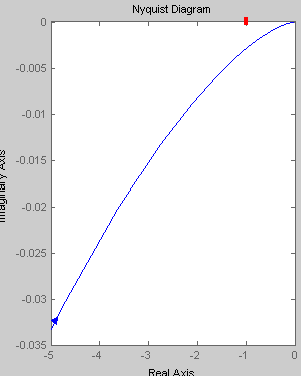
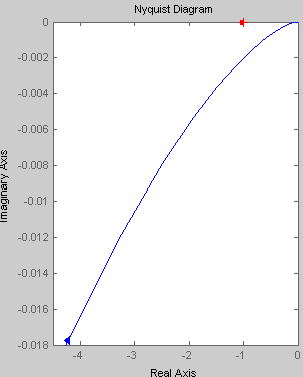
K=50 T=0.01 ξ=0.01 hуст	K=100 T=0.01 ξ=0.01 hуст
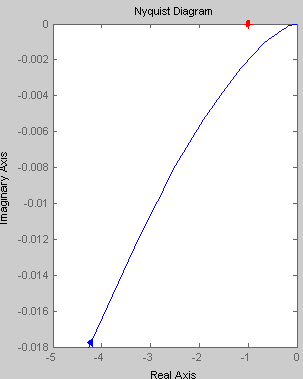
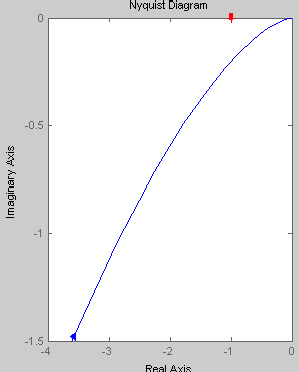
K=100 T=0.1 ξ=0.01 hуст	K=100 T=0.1 ξ=0.99 hуст

Переходный процесс колебательного звена второго порядка носит затухающий характер и стремится к своему установившемуся значению h_уст, которое равно коэффициенту усиления K. Таким образом при увеличении коэффициента К увеличивается установившееся значение h_уст выходного сигнала. Увеличение постоянной времени Т приводит к увеличению времени необходимого для достижения установившегося значения. Увеличение коэффициента демпфирования (дикримента затухания) приводит к уменьшению колебательности переходного процесса, а вместе с этим к уменьшению времени необходимого для достижения установившегося значения.

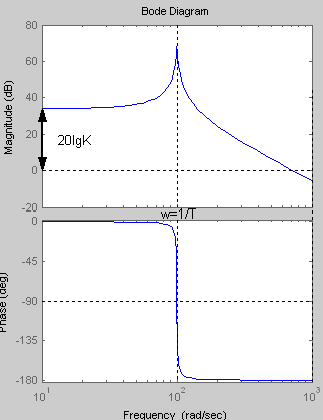
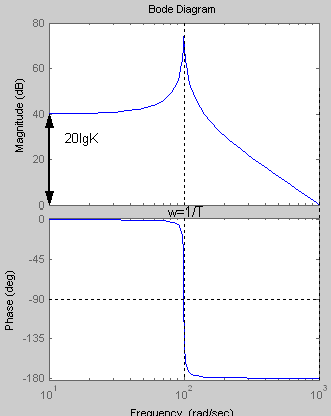
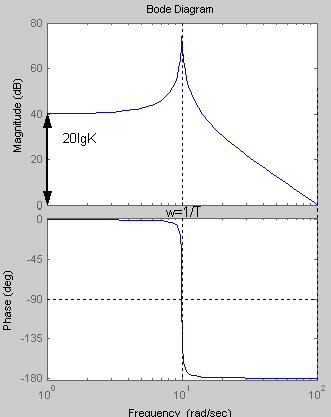
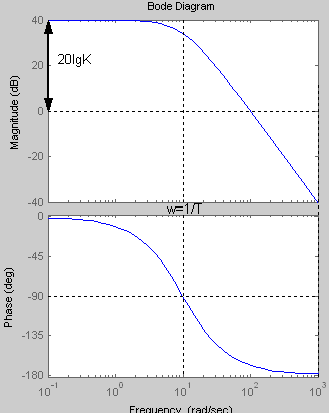
Логарифмическая амплитудная и фазовая частотные характеристики:
K=50 T=0.01 ξ=0.01	K=100 T=0.01 ξ=0.01
K=100 T=0.1 ξ=0.01	K=100 T=0.1 ξ=0.99

При увеличении коэффициента К увеличивается значение амплитуды, на фазу изменение коэффициента К не влияет. Увеличение постоянной времени Т приводит к уменьшению частоты сопряжения.

Коэффициент демпфирования вносит в ЛАХ скачок амплитуды в частоте сопряжения . Снижение данного коэффициента приводит к росту резонансного пика ЛАХ. С другой стороны чем больше коэффициент ξ , тем более пологий будет график ЛФХ.

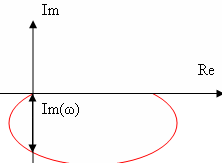
Амплитудно-фазовая частотная характеристика имеет вид:

K=50 T=0.01 ξ=0.01	K=100 T=0.01 ξ=0.01
K=100 T=0.1 ξ=0.01	K=100 T=0.1 ξ=0.99

При увеличении коэффициента К происходит увеличение годографа АФЧХ. Увеличение постоянной времени Т приводит к уменьшению годографа АФЧХ.

График АФЧХ колебательного звена пересекает мнимую ось в точке(0;Im(ω)), где . Чем больше коэффициент демпфирования (дикримент затухания) , тем меньше значение Im(ω), а следовательно меньше годограф АФЧХ.

3. Выводы

В данной работе были изучены временные и частотные характеристики 3-х типов динамических звеньев: интегрирующее, апериодическое первого порядка и колебательное второго порядка. Рассмотрели характер влияния изменения параметров системы на временные и частотные характеристики, построили графики соответствующих характеристик.