Лабораторная работа №2. Вариант №3

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФИЛИАЛ В Г. ИШИМБАЙ

Отчет по лабораторной работе №2

по предмету «Теория автоматического управления»

на тему: Анализ устойчивости системы автоматического регулирования.

Выполнил: студент гр. АТП-308

Шарипов Д.В.

Приняла: Перевертайло Ю.В.

Ишимбай 2006

1. Цель работы

Приобретение навыков в составлении сложных структурных схем систем автоматического регулирования с помощью пакета прикладных программ, определение ЛАХ и ЛФХ системы.

Анализ устойчивости системы по критерию Гурвица-Найквиста, определение границы устойчивости системы.

2. Выполнение работы

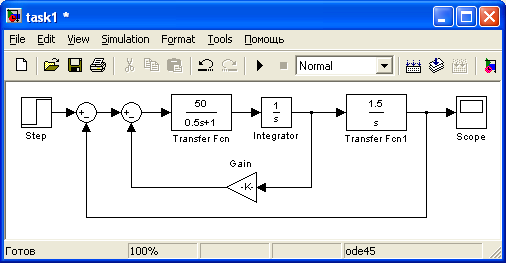
В соответствии с вариантом задания собрать структурную схему САУ (рис. 1).

Рис. 1

T₁ = 0.5сек T₂ = 0.25сек К₁ = 50 К₃ = 0.75 К₂ =?

Используя критерий устойчивости Гурвица, определить значение коэффициента передачи K₂ системы, при котором система будет находиться в устойчивом состоянии:

- передаточная функция системы

- характеристическое уравнение

Необходимое условие устойчивости () выполняется при .

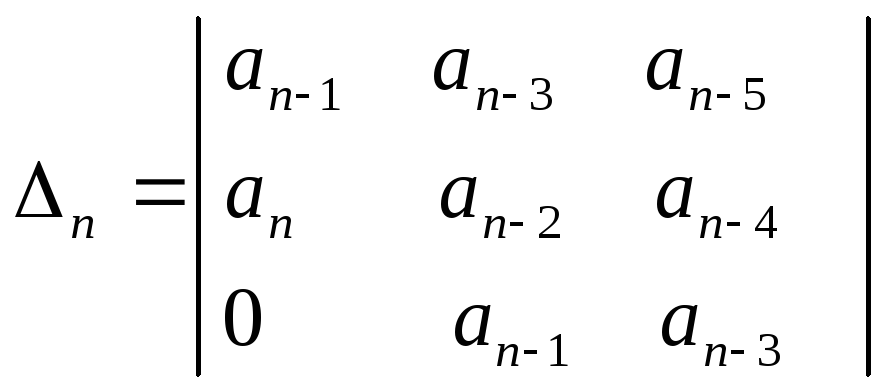- определитель Гурвица

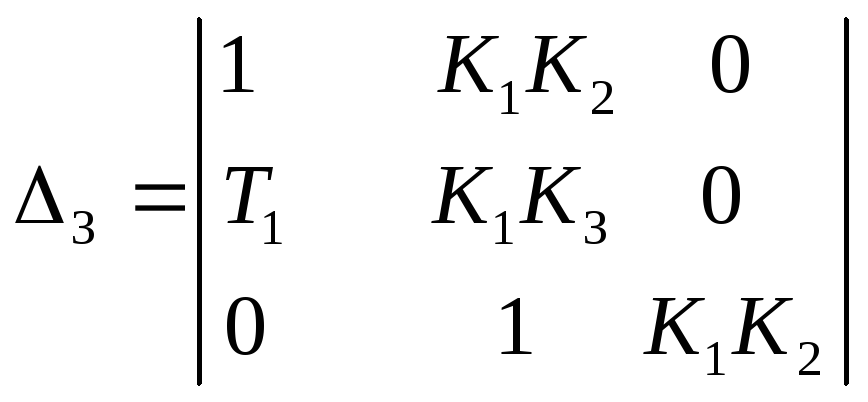
- диагональный минор второго порядка

- достаточное условие устойчивости для систем третьего порядка

Таким образом, при K₂<1.5 САУ будет находиться в устойчивом состоянии, при K₂=1.5 на границе устойчивости, при K₂>1.5 в неустойчивом состоянии.

Рассчитать с помощью пакета прикладных программ переходные, логарифмические и амплитудно-фазовые характеристики замкнутой и разомкнутой систем автоматического регулирования для трёх режимов работы: неустойчивого, на границе устойчивости, устойчивого, построить все полученные графики.

Замкнутая САУ Передаточная функция:
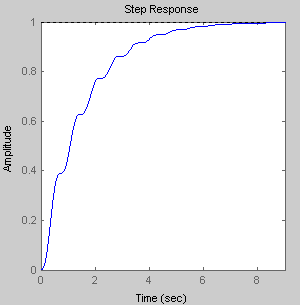
Переходный процесс
hуст	K2=0.5 Переходная функция h(t) с течением времени стремится к своему установившемуся значению hуст=1. Значит, система находится в устойчивом состоянии.

hуст	K2=1.5 Переходная функция h(t) носит характер незатухающих колебаний с постоянной амплитудой. Значит, система находится на границе устойчивости.
	K2=2 Переходная функция h(t) носит характер незатухающих колебаний с увеличивающейся амплитудой. Значит, система находится в неустойчивом состоянии.
Разомкнутая САУ Передаточная функция: Логарифмическая амплитудная и фазовая частотные характеристики
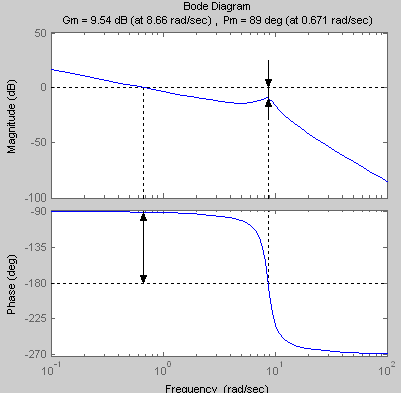
ωкр ωср Δφ ΔА	K2=0.5 ωср=0.671с-1 ωкр=8.66с-1 ωср< ωкр , значит, система находится в устойчивом состоянии. Запас устойчивости по амплитуде: (дБ) Запас устойчивости по фазе: (град)

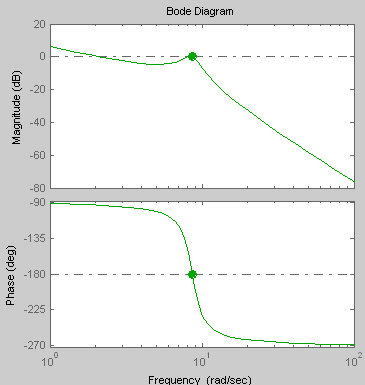
ωср ωкр	K2=1.5 ωср=ωкр=8.66 с-1 ωср=ωкр , значит, система находится на границе устойчивости
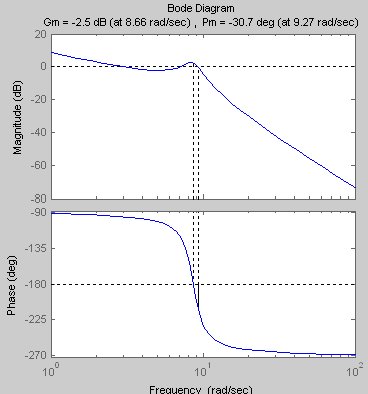
ωср ωкр	K2=2 ωср=9.27с-1 ωкр=8.66с-1 ωср> ωкр , значит, система находится в неустойчивом состоянии.

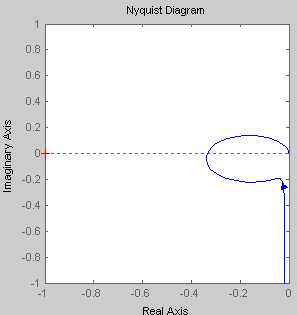
АФЧХ
	K2=0.5 Годограф АФЧХ разомкнутой системы не охватывает точку с координатами (-1;j0). Значит, исходя из критерия Найквиста, замкнутая система будет находиться в устойчивом состоянии.
	K2=1.5 Годограф АФЧХ разомкнутой системы проходит через точку с координатами (-1;j0). Значит, замкнутая система находится на границе устойчивости.
	K2=2 Годограф АФЧХ разомкнутой системы охватывает точку с координатами (-1;j0). Значит, замкнутая система находится в неустойчивом состоянии.

3. Выводы

В лабораторной работе были изучены критерии устойчивости Найквиста и Гурвица, а также оценка устойчивости по логарифмическим частотным характеристикам. С помощью этих критериев были исследованы на устойчивость САУ, определили их границы устойчивости. Результаты критериев полностью совпали. Определили коэффициенты запаса устойчивости по фазе и амплитуде.