Задания для самостоятельного решения
1. Привести к нормальному виду уравнения
следующих плоскостей: а)
;
б)
.
2. Найти расстояние от точки
до плоскости
.
Как расположена эта точка относительно
плоскости?
3. Найти длину перпендикуляра, опущенного
из точки
на плоскость
.
4. Найти уравнение плоскости, проходящей
через точки
и
и перпендикулярной плоскости
.
5. Найти уравнение плоскости, зная, что
точка
служит основанием перпендикуляра,
опущенного из начала координат на эту
плоскость.
6. Найти уравнения плоскостей, проходящих
через оси координат перпендикулярно
плоскости
.
7. Найти уравнение плоскости, точки
которой одинаково удалены от точек
и
.
8. Вычислить угол между плоскостями,
проходящими через точку
,
одна из которых содержит ось
,
а другая – ось
.
9. Найти уравнение плоскости, проходящей
через точку пересечения плоскостей
,
,
и через точки
и
.
10. Составить уравнение плоскости,
проходящей через линию пересечения
плоскостей
,
и через точку
.
11. Составить уравнение плоскости,
проходящей через линию пересечения
плоскостей
и
и отсекающей равные отрезки на осях
и
.
12. Составить уравнение плоскости,
проходящей через линию пересечения
плоскостей
и
и перпендикулярной плоскости
.
13. Составить уравнение плоскости,
проходящей через точку
и параллельной векторам
и
.
14. Известны координаты вершин тетраэдра:
,
и
.
Составить уравнение его граней.
15. Вычислить объем тетраэдра, данного в предыдущей задаче.
16. Проверить, можно ли провести плоскость
через следующие четыре точки:
и
.
3. Прямая
1. Прямая может быть задана уравнениями двух плоскостей
пересекающихся по этой прямой.
2. Исключив поочередно и из предыдущих уравнений, получим уравнения
.
Здесь прямая определена двумя плоскостями, проецирующими ее на плоскости и .
3. Уравнения прямой, проходящей через
две точки
и
,
имеют вид
. (1)
4. Так называемые канонические уравнения
(2)
определяют прямую, проходящую через
точку
и параллельную вектору
.
В частности, эти уравнения могут быть
записаны в виде
,
где
и
- углы, образованные прямой с осями
координат. Направляющие косинусы прямой
находятся по формулам
. (3)
5. От канонических уравнений прямой,
вводя параметр
,
нетрудно перейти к параметрическим
уравнениям:
(4)
6. Угол между двумя прямыми, заданными
их каноническими уравнениями
и
,
определяется по формуле
; (5)
условие параллельности двух прямых:
; (6)
условие перпендикулярности двух прямых:
.
(7)
7. Необходимое и достаточное условие нахождения двух прямых, заданных их каноническими уравнениями, в одной плоскости (условие компланарности двух прямых):
. (8)
Если величины
не пропорциональны величинам
,
то указанное соотношение является
необходимым и достаточным условием
пересечения двух прямых в пространстве.
8. Угол между прямой и плоскостью определяется по формуле
; (9)
условие параллельности прямой и плоскости:
; (10)
условие перпендикулярности прямой и плоскости:
. (11)
9. Для определения точки пересечения
прямой
с плоскостью
нужно решить совместно их уравнения,
для чего следует воспользоваться
параметрическими уравнениями прямой
:
а) если
,
то прямая пересекает плоскость;
б) если
и
,
то прямая параллельна плоскости;
в) если
и
,
то прямая лежит в плоскости.
Пример 1. Уравнения прямых
и
привести к каноническому виду.
Решение.
1 способ. Исключив сначала , а затем , имеем
и
.
Если разрешить каждое из уравнений относительно , то получим
,
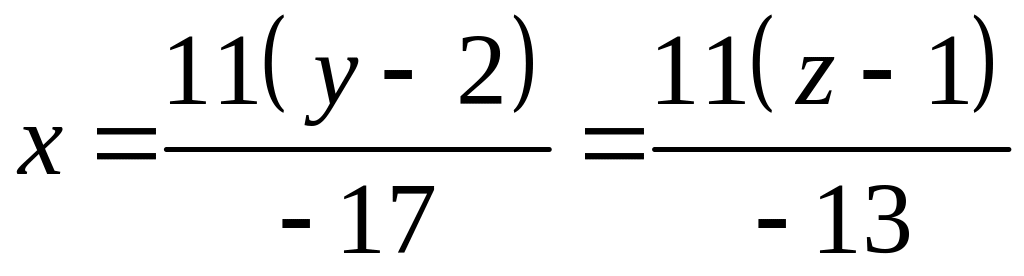т.е.
.
11 способ. Найдем вектор
,
параллельный искомой прямой. Так как
он должен быть перпендикулярен нормальным
векторам
и
заданных плоскостей, то за
можно принять векторное произведение
векторов
и
:
.
Таким образом,
.
В качестве точки
,
через которую проходит искомая прямая,
можно взять точку пересечения ее с любой
из координатных плоскостей, например
с плоскостью
.
Так как при этом
,
то координаты
и
этой точки определяются из системы
уравнений заданных плоскостей, если в
них положить
:
Решая эту систему, находим
.
Итак, искомая прямая определяется уравнениями
.
Пример 2. Построить прямую
Решение.
Искомую прямую можно построить как линию пересечения плоскостей. Для этого запишем уравнения этих плоскостей в отрезках на осях:
,
.
Построив данные плоскости, получим искомую прямую.
Пример 3. Из начала координат опустить
перпендикуляр на прямую
.
Решение.
Используя условие (11) перпендикулярности
прямой и плоскости и полагая
,
составим уравнение плоскости, проходящей
через начало координат и перпендикулярной
заданной прямой. Это уравнение имеет
вид
.
Найдем точку пересечения этой плоскости и данной прямой. Параметрически уравнения прямой запишутся так:
.
Для определения имеем уравнение
,
откуда
.
Координаты точки пересечения
,
т.е.
.
Остается составить уравнения прямой, проходящей через начало координат и через точку ; используя соотношения (1), получим
,
или
.
Пример 4. В уравнениях прямой
определить параметр
так, чтобы эта прямая пересеклась с
прямой
,
и найти точку их пересечения.
Решение.
Для нахождения параметра
используем условие (8) пересечения двух
прямых; полагая
,
получим
,
или
,
т.е.
.
Чтобы найти координаты точки пересечения прямых
и
,
выразим из первых уравнений и через :
,
.
Подставляя эти значения в равенство
,
имеем
,
откуда
.
Зная
,
находим
,
.
Следовательно,
.
Пример 5. Составить уравнения прямой,
проходящей через точку
и пересекающей ось
под прямым углом.
Решение.
Так как прямая перпендикулярна оси
и пересекает ее, то она проходит через
точку
.
Составив уравнения прямой, проходящей
через точки
и
,
получаем
,
т.е.
.
Пример 6. Дана плоскость
и вне нее точка
.
Найти точку
,
симметричную точке
относительно данной плоскости.
Решение.
Запишем уравнения любой прямой, проходящей через точку :
.
Координаты
направляющего вектора прямой,
перпендикулярной плоскости, можно
заменить координатами нормального
вектора
данной плоскости. Тогда уравнения этой
прямой запишутся в виде
.
Найдем проекцию точки на данную плоскость, решив совместно уравнения
.
Перепишем уравнения прямой в виде
.
Подставляя эти выражения для
,
и
в уравнение плоскости, найдем
,
откуда
,
,
.
Координаты симметричной точки найдутся из формул
,
,
,
т.е.
,
,
,
откуда
.
Следовательно,
.
Пример 7. Дана прямая
и вне нее точка
.
Найти точку
,
симметричную точке
относительно данной прямой.
Решение.
Уравнение плоскости, проецирующей точку на данную прямую, имеет вид
.
Координаты нормального вектора
плоскости, перпендикулярной прямой,
заменим координатами направляющего
вектора
данной прямой; тогда получим
,
или
.
Найдем проекцию точки на прямую, для чего совместно решим систему уравнений
.
Параметрические уравнения данной прямой имеют вид
,
,
.
Подставляя
,
и
в уравнение плоскости, найдем
.
Отсюда
.
Тогда координаты симметричной точки можно найти, используя формулы для координат середины отрезка, т.е.
,
,
,
откуда
.
Итак,
.
Пример 8. Через прямую
провести плоскость, параллельную прямой
.
Решение.
Запишем уравнения первой из заданных прямых с помощью уравнений двух плоскостей, проецирующих ее соответственно на плоскости и :
,
или
;
,
или
.
Уравнение пучка плоскостей, проходящих через эту прямую, имеет вид
,
или
.
Используя условие параллельности прямой и плоскости, определим так, чтобы соответствующая плоскость пучка была параллельна второй из заданных прямых. Имеем
,
или
,
откуда
.
Таким образом, искомая плоскость определяется уравнением
.
Пример 9. Найти уравнения проекции
прямой
на плоскость.
Решение.
Запишем уравнения заданной прямой в виде уравнений двух плоскостей, проецирующих ее соответственно на плоскости и :
,
или
;
,
или
.
Уравнение пучка плоскостей, проходящих через данную прямую, запишется в виде
,
или
.
Используя условие перпендикулярности плоскостей, выберем из этого пучка плоскость, проецирующую данную прямую на заданную плоскость. Имеем
,
или
,
откуда
.
Итак, уравнение проецирующей плоскости имеет вид
,
или
.
Искомую проекцию можно определить как линию пересечения двух плоскостей – заданной и проецирующей:
Приведя эти уравнения прямой к каноническому виду, окончательно получим
,
т.е.
.