Добавил:

Studfiles2 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уфимский Государственный Авиационный Технический Университет

Предмет:

Теория автоматического управления

Файл:

Методичка по лабораторной работе №3

.DOC

Скачиваний:

Добавлен:

02.05.2014

Размер:

211.46 Кб

Скачать

☆

ЛАБОРАТОРНАЯ РАБОТА T28-3

КОРРЕКЦИЯ СТАТИЧЕСКИХ И ДИНАМИЧЕСКИХ СВОЙСТВ САУ

1. ЦЕЛЬ РАБОТЫ

Эта работа нацелена на приобретение студентами навыков анализа и синтеза САУ :

1) определение характеристик САУ, которые необходимо скорректировать;

2) обеспечение точности (уменьшение статической ошибки) САУ;

3) выбор значений параметров регулятора, обеспечивающих желаемые динамические свойства САУ;

4) подтверждение (путем моделирования) того, что в результате введения корректирующего устройства (регулятора) САУ приобрела желаемые свойства.

2. КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ•

Коррекция статических и динамических свойств САУ имеет своей целью повышение статической и динамической точности отработки системой задающего воздействия (или парирование возмущающего воздействия), повышение запасов ее устойчивости. Наиболее распространенными способами коррекции свойств САУ является изменение коэффициента усиления ее разомкнутой части, введение в САУ новых звеньев (как правило, интегрирующего или дифференцирующего типа), охват объекта управления местной обратной связью.

2.1. Коррекция статических свойств САУ

Статические свойства системы определяется величиной установившейся ошибки вызванной действием задающего воздействия и определяемой по формуле

(3.1)

Величины называются коэффициентами ошибок и определяются по формулам:

(3.2)

где - передаточная функция САУ по ошибке управления, равная

(3.3)

- передаточная функция разомкнутой САУ.

Основными способами уменьшения статической ошибки системы являются:

1) увеличение коэффициента усиления прямого тракта системы;

2) введение в прямой тракт система интегрирующих звеньев;

3) охват объекта управления местной неединичной положительной обратной связью.

Представим структурную схему системы в виде, изображенном на рис. 3.1 где через обозначена передаточная функция неизменяемой части системы

(3.4)

Здесь и далее полагается, что - изменяемый коэффициент усиления регулятора системы.

Первые два коэффициента ошибок и определяется выражениями:

(3.5)

(3.6)

Из (3.5) и (3.6) с учетом (3.1) вытекает, что с увеличением K статическая ошибка в системе уменьшается и наоборот, с уменьшением K статическая ошибка в системе увеличивается.

Введем в прямой тракт системы одно интегрирующее звено (рис. 3.2). В этом случае .

Так как то система на рис. 3.2 является астатической (с астатизмом первого порядка). Система имеет нулевую статическую ошибку при отработке постоянного задающего воздействия и постоянную, обратно пропорциональную K, ошибку при отработке линейно изменяющегося воздействия .

W(s)

K/s

W(s)

g(t) ε(t) y(t) g(t) ε(t) y(t)

Рис. 3.1 Рис. 3.2

Охватим неизменяемую часть системы местной неединичной положительной обратной связью с коэффициентом усиления (рис.3.3). Тогда эквивалентная передаточная функция неизменяемой части системы равна

(3.7)

Если коэффициент усиления K выбрать из условия

(3.8)

то свободный коэффициент полинома знаменателя

обратится в нуль и приобретает интегрирующие свойства:

(3.9)

Следовательно, замкнутая система становится астатической (с астатизмом 1-го порядка). Отсюда =0, а коэффициент будет равен

(3.10)

K_ос

W_экв(s)

W(s)

g(t) ε(t) y(t)

Рис. 3.3

2.2. Коррекция динамических свойств САУ

Улучшение динамических свойств САУ заключается в увеличении быстродействия САУ (уменьшении времени регулирования t_рег), уменьшении перерегулирования (см. рис. 3.4), а также увеличении запасов устойчивости по фазе и по модулю (см. лабораторную работу УТС-2). При этом

где -максимальное значение переходной характеристики замкнутой САУ ;

- установившееся значение .

Время регулирования t_рег - минимальная величина, при которой удовлетворяется условие:

где - заданная величина ошибки (обычно =0,05).

h(t)

2δ

h_уст

h_max

t_рег

Рис. 3.4

Одним из эффективных средств достижения этой цели является уменьшение отрицательных фазовых сдвигов в прямом тракте системы путем охвата неизменяемой части системы местными отрицательными обратными связями.

На рис. 3.5 R(s) представляет собой передаточную функцию регулятора САУ, которая считается заданной.

K_ос

W_экв(s)

W(s)

R(s)

(t) ε(t) u(t) y(t)

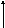
Рис. 3.5

Пусть неизменяемая часть системы представляет собой апериодическое звено первого порядка, т.е.

(3.11)

Тогда передаточная функция эквивалентного объекта управления равна

(3.12)

где и - коэффициент усиления и постоянная времени эквивалентного объекта, равные:

(3.13)

(3.14)

Из (3.14) следует, что соответствующим выбором постоянную времени

эквивалентного объекта можно уменьшить в (1+) раз по сравнении с постоянной времени объекта без местной обратной связи. Тем самым уменьшаются отрицательные фазовые сдвиги, вносимые прямым трактом системы, что приводит к увеличению запасов устойчивости системы. При этом, однако, уменьшается в (1+) раз коэффициент усиления эквивалентного объекта по сравнению с коэффициентом усиления объекта без местной обратной связи. Это нежелательно, так как приводит к уменьшению быстродействия системы вследствие уменьшения общего коэффициента усиления прямого тракта системы. В этом случае с целью обеспечения необходимого быстродействия системы увеличивают коэффициент усиления регулятора.

3. СОДЕРЖАНИЕ РАБОТЫ

3.1. При исследовании способов коррекции статических свойств САУ в качестве исходных данных выступают передаточная функция неизменяемой части системы вида

(3.15)

и задающие воздействия вида

а) б)

в соответствии с задаваемым преподавателем вариантом работы (см. таблицу).

В процессе выполнения этой части работы студенты должны:

путем моделирования на РС исходной САУ (рис. 3.6) получить

графики

2) сравнить полученную таким образом экспериментальную величину с теоретической, вычисленной по формула (3.1);

3) применяя описанные в теоретической части методических указаний способы коррекции статических свойств (см. п.2.1), обеспечить требуемую статическую ошибку системыпри отработке задающего воздействия

4) получить графики и в скорректированной системе для

а) б).

5) сравнить время регулирования и перерегулирование в исходной и скорректированной системах при

3.2. При исследовании рассмотренного способа коррекции динамических свойств САУ (см. п. 2.2) в качестве исходных данных выступают передаточная функция неизменяемой части системы вида (3.15) и передаточная функция регулятора вида

(3.16)

Задающее воздействие .

В процессе выполнения данной части работы студенты должны:

получить путем моделирования на РС графики , в системе

(рис. 3.7);

2) определить время регулирования и перерегулирование , а также запасы устойчивости в исходной системе;

3) применяя описанный выше способ коррекции динамических свойств САУ, найти экспериментально (путем последовательного перебора) значение , обеспечивающее в системе заданные преподавателем показатели качества (,)и запасы устойчивости (при необходимости увеличить коэффи- циент);

4) получить графики , , а также ЛАХ и ЛФХ разомкнутой системы в скорректированной САУ.

W(s)

R(s)

W(s)

(t) ε(t) y(t) g(t) ε(t) u(t) y(t)

Рис. 3.6 Рис. 3.7

Таблица

№ варианта Параметры	1	2	3	4	5	6	7	8
a	0,5	1,0	1,5	2,0	2,5	3,0	3,5	4,0
K₀	1	2	3	4	5	6	7	8
T, c	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
ξ	0,6	0,7	0,8	0,8	0,7	0,9	0,5	0,4
	0	0	0,05	0	0,10	0,07	0	0
t_рег, c ≤	1,3	1,5	2,0	2,5	3,0	3,5	4,0	4,0
, % ≤	0	10	10	5	5	5	0	0