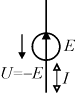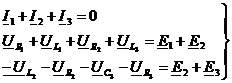1.1-1.4
Электротехника - наука о чем? Что лежит в основе электротехники для решения широкого круга инженерных задач? ТОЭ – наука о практических применениях электрических и магнитных явлений. Изучает: электрические цепи, электротехнические устройства и машины предназначенные для генерации, передачи и преобразование электрической энергии и сигналов. |
Электрическая цепь ,её составные части. Что характеризует элемент цепи. Электрическая цепь – это совокупность устройств и объектов, создающих путь для электрического тока, процессы в этой цепи могут быть описаны с помощью понятий об электрическом токе, напряжении и ЭДС. Элементы цепи. Пассивные: резистор, катушка, конденсатор. Активные: источник тока, источник напряжения. |
Электрический ток, напряжение, ЭДС, энергия, мощность. Их взаимные связи. Напряжение – скалярная величина, равная линейному интегралу напряжения электрического поля при перемещении заряда между точками. Электрический ток – направленное движение электрических зарядов. ЭДС – способность стороннего или индуцированного электрического поля создавать электрический ток. Энергия – способность электрического поля совершать работу. Мощность – скорость изменения электрической энергии. |
Топологические элементы электрической цепи. Законы Кирхгофа. Ветвь – это участок цепи на которой протекает один и тот же ток. Узел – это место соединения трех или более ветвей. Контур – это замкнутый путь из ветвей, начинающийся и заканчивающийся в одном и том же узле. Законы Кирхгова. Алгебраическая сумма электрических токов в узле равна нулю. Алгебраическая сумма напряжений в любом контуре электрической цепи равна алгебраической сумме ЭДС действующих в этом контуре. |
1.5 Пассивные элементы:
Основные элементы электрической цепи, используется понятие идеализированные элементы.
Сопротивлением называется идеализированный элемент цепи, приближенно заменяющий резистор, в котором происходит необратимый процесс преобразования электрической энергии в тепловую. Буквенное обозначение – R или r.
Между напряжением на элементе, током и сопротивлением элемента существует соотношение:
![]() , (1.2)
, (1.2)
Величина сопротивления измеряется в омах (Ом). [Ом] = [В/А]. Сопротивление всегда положительное, т.е., направления тока через сопротивление и напряжения на нем совпадают.
Емкостью называется идеализированный элемент электрической цепи, приближенно заменяющий конденсатор, в котором накапливается энергия электрического поля. Буквенное обозначение емкости – С. Величина емкости определяет, какой заряд q можно получить при заданном напряжении u:
![]() (1.3)
(1.3)
или
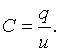
Величина емкости измеряется в фарадах (Ф).
Если контур из проводника поместить в переменное магнитное поле, то согласно закону электромагнитной индукции (Фарадея – Максвелла) в нем наводится электродвижущая сила (ЭДС), равная:
![]() (1.7)
(1.7)
где Ф – магнитный поток, пронизывающий контур.
Измеряется поток в веберах (Вб). Согласно выражению (1.7)
![]() .
.
Предположим, что контур состоит из нескольких витков (катушка), каждый из которых пронизывается своим потоком Фi.
Из (1.7) имеем:
![]() , (1.7а)
, (1.7а)
где – потокосцепление, равное сумме всех потоков, пронизывающих все отдельные витки контура.
1.6 Активные элементы:
Источники
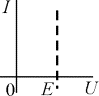
ЭДС - это двухполюсники, у которых
разность потенциалов на выходе не
зависит от величины и направления
протекания тока, т.е. их вольтамперные
характеристики (ВАХ) представляют собой
прямые л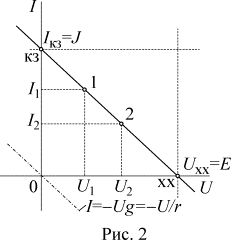 инии
параллельные оси I
инии
параллельные оси I
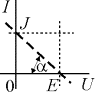
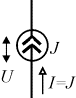
Источники тока - это двухполюсники, у которых протекающий через них ток не зависит от знака и значения разности потенциалов на выходе, т.е. их ВАХ представляют собой прямые линии параллельные оси U. Отсюда, сопротивление источника тока равно бесконечности, а проводимость - нулю.
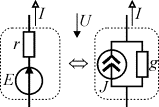
Реальному источнику электрической энергии соответствует схема замещения, состоящая из идеального источника ЭДС E и резистивного элемента, сопротивление Rвт которого равно внутреннему сопротивлению источника
Поэтому, чем меньше внутреннее сопротивление источника эдс , тем ближе его свойства к свойствам идеального источника.
|
Идеальные источники |
Источники электрической энергии |
|
ЭДС |
Тока |
||
ВАХ |
|
|
|
Эл. схема |
|
|
|
Параметры |
|
|
|
1.7
Теория цепей имеет два направления:
анализ электрических цепей
синтез (создания новых) электрических цепей.
При анализе электрической цепи, ее топология (схема), как правило, нам известна. В большинстве случаев известны даже номиналы всех электронных компонентов цепи, но не всегда. И наша задача рассчитать все (или часть) токов и напряжений. Если неизвестны параметры каких-то компонентов цепи, то их нужно рассчитать. Со всеми этими задачами справиться можно, если хорошо владеть методиками расчета электрических цепей.
Синтез электрических цепей задача более сложная и неоднозначная. При создания новой цепи мы еще не знаем с каких элементов она будет состоять, какие у них номиналы и как эти элементы будут соединены между собой (мы не знаем топологии). Более того, иногда (очень редко) мы даже не знаем можно ли при данном техническом уровне ее вообще реализовать. Чаще всего решений построения цепи может быть очень-много (нас ограничивает только наша фантазия и знания). Между многими решениями мы выбираем то, которое больше всего подходит нам по финансам, элементной базе, массе и габаритам. Реже всего решений может вообще не бытьесли принципы роботы нашей цепи нарушают фундаментальные законы физики, а мы все же пытаемся ее создать.
При синтезе цифровых логических схем используют уже хорошо наработанные методы дискретной математики (булевая алгебра, минимизация логических функций и т.д.).
При синтезе аналоговых цепей используют два направления синтеза:
1) по известным операторным функциям, по Z(p) для двухполюсников и по передаточной функции для четырехполюсников;
2) по временным характеристикам, т.е. по известному временному отклику системы при воздействии импульса, обычно прямоугольной формы.
1.8
Для формирования уравнений электрического равновесия используются законы Кирхгофа и компонентные уравнения. На практике применяют методы, позволяющие упростить формирование уравнений электрического равновесия: методы контурных токов, узловых напряжений, переменных состояния, методы, основанные на использовании теорем теории цепей.
Система уравнений электрического равновесия может быть преобразована в одно дифференциальное или алгебраическое уравнение относительно одного неизвестного тока или напряжения. Дифференциальное уравнение содержит информацию о характере процессов в цепи и является основой для классификации цепей. Тип дифференциального уравнения определяется топологией цепи и характером входящих в неё элементов.
Классификация электрических цепей
Электрические цепи могут быть классифицированы по ряду признаков
по топологическим особенностям: планарные – непланарные (плоские –объёмные), разветвлённые – неразветвлённые, простые – сложные и т.д.
по энергетическим свойствам: активные – пассивные,
по числу внешних выводов: двухполюсники, трёхполюсники, многополюсники.
Система уравнений электрического равновесия преобразуется в одно уравнение, вид которого определяется свойствами цепи.
Классификация цепей производится в зависимости от вида уравнения электрического равновесия.
1.9
1.Входные воздействия и их классификации.2 Какие воздействия называются сигналами? 3. Почему гармонические воздействия широко применяются в технике? 4. Действующее значение периодического тока, напряжения, ЭДС.
3)Гармоническим воздействием называется функция, изменяющаяся по закону синуса или косинуса.
![]()
![]()
Гармонические воздействия являются основным видом возмущений и реакций в энергетических сетях и системах.
Действующее значение переменного тока - это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.
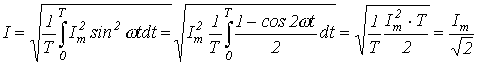
Im-амплитудное значение
Аналогичный
результат можно получить для синусоидальных
ЭДС и напряжений. Таким образом,
действующие значения синусоидальных
тока, ЭДС и напряжения меньше своих
амплитудных значений в ![]() раз:
раз:
![]()
Вместо Xи Xm – U (Um) илиE(Em)
2.1 синусоидальный ток характеризуется амплитудой Im и периодом T. Амплитуда синусоидального сигнала равна половине размаха изображения по вертикали.
2.2 Комплексное представление синусоидальных электрических величин сочетает наглядность векторных диаграмм с проведением точных аналитических расчётов цепей.
Комплексная амплитуда — комплексная величина, модуль и аргумент которой равны соответственно амплитуде и начальной фазе гармонического сигнала.
2.3
Закон Ома в комплексной форме получаем из формулы для комплексного сопротивления:
![]()
По первому закону Кирхгофа, алгебраическая сумма мгновенных значений токов, сходящихся в любом узле схемы, равна нулю:
![]()
Равенство не нарушится, если вместо токов подставить соответствующие комплексы. Это и будет выражение для первого закона Кирхгофа в комплексной форме:
![]()
где
![]() -
количество ветвей, подходящих к узлу.
-
количество ветвей, подходящих к узлу.
По второму закону Кирхгофа, в любом (замкнутом) контуре справедливо равенство алгебраических сумм мгновенных значений напряжений на сопротивлениях контура и ЭДС:
![]()
Заменив напряжения и ЭДС на соответствующие комплексы, получим выражение для второго закона Кирхгофа в комплексной форме:
![]()
где
![]() -
количество элементов в контуре,
-
количество элементов в контуре,
![]() -
количество ЭДС в контуре.
-
количество ЭДС в контуре.
Пример:
|
|
2.4
2.6 Представление синусоидальных ЭДС, напряжений и токов комплексными числами
Пусть мгновенная ЭДС задаётся уравнением:
![]() .
(2.20)
.
(2.20)
На комплексной плоскости вращающийся вектор:
![]() .
(2.21)
.
(2.21)
Мгновенная фаза:
![]() .
(2.22)
.
(2.22)
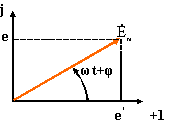
Рисунок 2.7 - Изображение синусоидального напряжения на комплексной плоскости
Мнимая составляющая комплексного числа вектора на комплексной плоскости определяет синусоидальное изменение ЭДС и обозначается символом Im.
![]() .
(2.23)
.
(2.23)
Комплексное
число
![]() удобно
представить в виде произведения двух
комплексных чисел
удобно
представить в виде произведения двух
комплексных чисел
![]() .
(2.24)
.
(2.24)
Комплексное число Ėm, соответствующее положению вектора в начальный момент времени называют комплексной амплитудой:
![]() .
(2.25)
.
(2.25)
Комплексное число ej∙ω∙t является оператором поворота вектора на угол ω∙t относительно начального положения вектора.
Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака ? произведения комплекса амплитуды Ėm и оператора вращения ej∙ω∙t :
![]() .
(2.26)
.
(2.26)
Переход от одной формы записи, к другой, осуществляется с помощью формулы Эйлера:
![]() ,
(2.27)
,
(2.27)
где
![]() -
показательная (полярная) форма,
-
показательная (полярная) форма,
![]() -
тригонометрическая.
-
тригонометрическая.
Чтобы преобразовать в показательную:
![]() ,
,
![]() .
(2.28)
.
(2.28)
Применение комплексных чисел позволяет от геометрического сложения или вычитания векторов на векторной диаграмме перейти к алгебраическому действию над комплексными числами этих векторов.
Если гармонически изменяющаяся величина представлена в виде косинусоидальной функции времени:
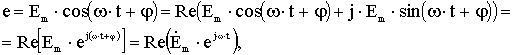 (2.29)
(2.29)
то её мгновенное значение равно действительной части произведения комплексной амплитуды и оператора вращения.
2.5-2.6
Вопрос
2.5. (Комплексное сопротивление и
проводимость участка цепи)
Р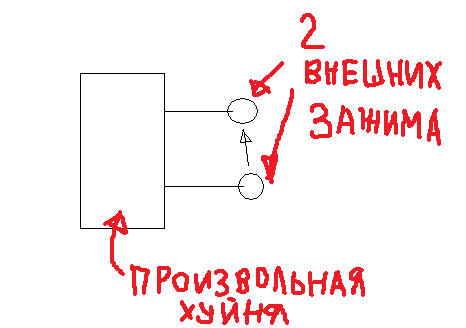 ассмотрим
произвольную линейную цепь с
сосредоточенными параметрами, находящуюся
под гармоническим воздействием. Выделим
участок этой цепи, имеющий два внешних
зажима, и не содержащий источников
энергии (рис. 1). Ток
ассмотрим
произвольную линейную цепь с
сосредоточенными параметрами, находящуюся
под гармоническим воздействием. Выделим
участок этой цепи, имеющий два внешних
зажима, и не содержащий источников
энергии (рис. 1). Ток ![]() и
напряжение
и
напряжение ![]() на
зажимах этого участка являются
гармоническими функциями времени:
на
зажимах этого участка являются
гармоническими функциями времени:
![]()
![]()
П![]() о
определению, комплексным
сопротивлением
о
определению, комплексным
сопротивлением ![]() пассивного
участка цепи называется отношение
комплексной амплитуды напряжения на
зажимах участка цепи к комплексной
амплитуде тока:
пассивного
участка цепи называется отношение
комплексной амплитуды напряжения на
зажимах участка цепи к комплексной
амплитуде тока:
Выражая комплексные амплитуды
н![]()
![]()
![]()
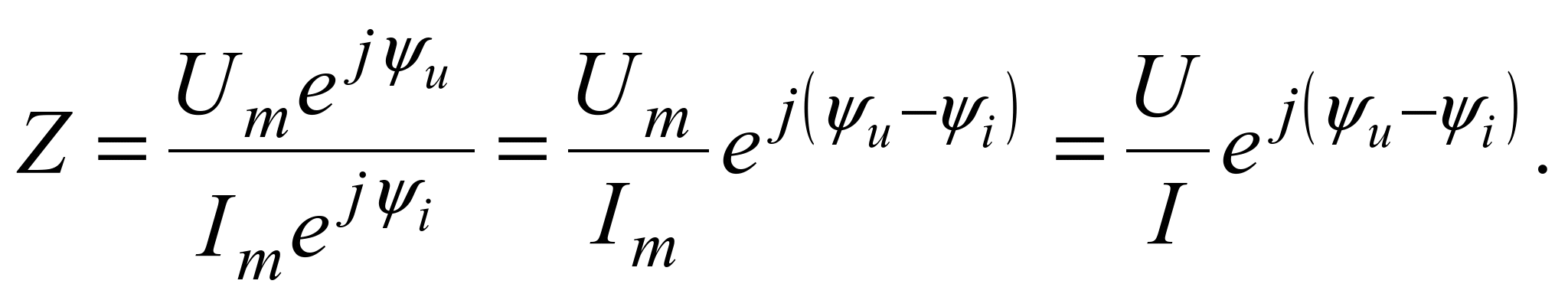 апряжения
и тока через соответствующие комплексные
действующие значения
апряжения
и тока через соответствующие комплексные
действующие значения ![]()
![]() получаем
еще и такую формулу:
Комплексное
входное сопротивление пассивного
участка цепи представляет собой
комплексное число, поэтому оно может
быть представлено в показательной
или
алгебраической
формах.
Величины
получаем
еще и такую формулу:
Комплексное
входное сопротивление пассивного
участка цепи представляет собой
комплексное число, поэтому оно может
быть представлено в показательной
или
алгебраической
формах.
Величины ![]() и
и ![]() называются
соответственно модулем и аргументом
комплексного сопротивления, величины
называются
соответственно модулем и аргументом
комплексного сопротивления, величины ![]() и
и ![]() –
его вещественной (резистивной) и мнимой
(реактивной) составляющими (модуль
комплексного входного сопротивления
цепи
–
его вещественной (резистивной) и мнимой
(реактивной) составляющими (модуль
комплексного входного сопротивления
цепи ![]() называется
также полным входным сопротивлением).
Представляя в показательной форме,
находим
называется
также полным входным сопротивлением).
Представляя в показательной форме,
находим
У![]() станавливаем,
что модуль комплексного сопротивления
станавливаем,
что модуль комплексного сопротивления ![]() равен
отношению амплитуд или действующих
значений напряжения и тока на зажимах
рассматриваемого участка цепи:
равен
отношению амплитуд или действующих
значений напряжения и тока на зажимах
рассматриваемого участка цепи:
а![]() аргумент равен разности начальных фаз
напряжения и тока:
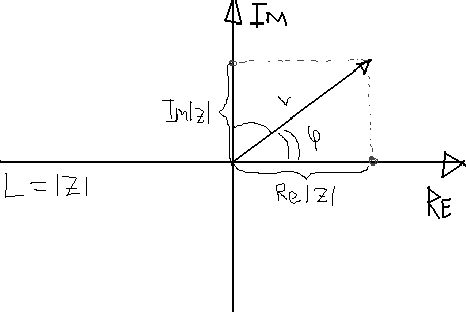
Комплексное
входное сопротивление может быть
представлено в виде вектора, расположенного
в комплексной плоскости, длина которого
в определенном масштабе, равна
,
а угол наклона к положительной вещественной
полуоси равен
аргумент равен разности начальных фаз
напряжения и тока:
Комплексное
входное сопротивление может быть
представлено в виде вектора, расположенного
в комплексной плоскости, длина которого
в определенном масштабе, равна
,
а угол наклона к положительной вещественной
полуоси равен ![]() (рисунок
2) Вещественная
и
мнимая
составляющие
входного сопротивления
представляют
собой проекции вектора
на
вещественную и мнимую оси
соответственно:
(рисунок
2) Вещественная
и
мнимая
составляющие
входного сопротивления
представляют
собой проекции вектора
на
вещественную и мнимую оси
соответственно:
![]()
![]()
 Величина,
обратная комплексному входному
сопротивлению, называется комплексной
входной проводимостью участка
цепи
Величина,
обратная комплексному входному
сопротивлению, называется комплексной
входной проводимостью участка
цепи
![]() Комплексная
входная проводимость (комплексная
проводимость) может быть определена
как отношение комплексных амплитуд или
комплексных действующих значений тока
и напряжения на зажимах рассматриваемого
участка цепи:
Комплексная
входная проводимость (комплексная
проводимость) может быть определена
как отношение комплексных амплитуд или
комплексных действующих значений тока
и напряжения на зажимах рассматриваемого
участка цепи:
![]()
![]() И в показательной форме
И в показательной форме
М![]() одуль
комплексной входной проводимости
одуль
комплексной входной проводимости ![]() является
величиной, обратной модулю комплексного
входного сопротивления, а аргумент
входной проводимости
является
величиной, обратной модулю комплексного
входного сопротивления, а аргумент
входной проводимости ![]() равен
по абсолютному значению и противоположен
по знаку аргументу комплексного входного
сопротивления
равен
по абсолютному значению и противоположен
по знаку аргументу комплексного входного
сопротивления ![]() .
Комплексная
входная проводимость участка цепи может
быть также представлена в алгебраической
форме
.
Комплексная
входная проводимость участка цепи может
быть также представлена в алгебраической
форме ![]() . Здесь
. Здесь ![]() и
и ![]() -вещественная
(резистивная) и мнимая (реактивная)
составляющие входной проводимости,
которые можно рассматривать как проекции
вектора
-вещественная
(резистивная) и мнимая (реактивная)
составляющие входной проводимости,
которые можно рассматривать как проекции
вектора ![]() на
вещественную и мнимую оси комплексной
плоскости
на
вещественную и мнимую оси комплексной
плоскости
![]() ,
, ![]() .
Вопрос
2.6. (Последовательное соединение R,L,C -
элементов)
.
Вопрос
2.6. (Последовательное соединение R,L,C -
элементов)
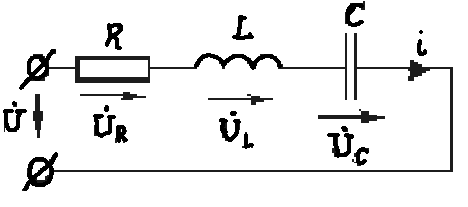
На основании второго закона Кирхгофа
U
= UR + UL + UC => U = IR +L![]() +
+![]()
Перейдем к комплексным изображениям:
I
= Im sin(t+i) ![]() .
.
Используя полученный комплекс тока, определим комплексы падения напряжения на участках цепи:
для
сопротивления![]() для
индуктивности
для
индуктивности 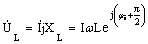
для
емкости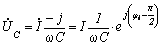
Найденные
комплексы ![]() ,
,![]() ,
,![]() подставим
в исходное уравнение
подставим
в исходное уравнение

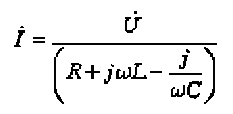
Закон Ома в комплексной форме.
Выражение в знаменателе представляет собой комплексное сопротивление исходной цепи, которое имеет вещественную и мнимую составляющую
![]() ,
где
,
где 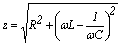 ;
;  .
.
Для комплексных амплитуд закон Ома запишется в следующем виде:
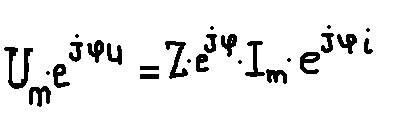 ,где
Um= ImZ амплитуда
напряжения
,где
Um= ImZ амплитуда
напряжения
2.7 Методика расчета эл. цепей комплексн. методом.
Для всех реактивных элементов определяется их комплексное сопротивлении
Все токи и напряжения рассматриваются в виде комплексных амплитуд.
w-омега v- фи
U(t) = Um*sin(wt+v)
U(t) = Um*exp(i*(wt+v) = Um* exp(iv)*exp(iwt)
U = Um*exp(iv) – комплекс амплитуда
U = Um*exp(iv)/sqrt(2) - комплексное напряжение
U= |U| v = arg( U)
V = arctg(мнимая/реальную)
Сопротивление Rl = jwl, Rc= 1/jwc, Rr = R.
3.1 Метод эквивалент преобразований.
Заключ-ся в преобразов эл цепи, содержащ 1 источник и 1 сопротивление.
послед соед-е R
![]()

![]()
паралельн соед
![]()
Преобразование источников
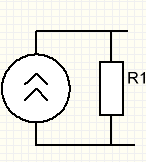
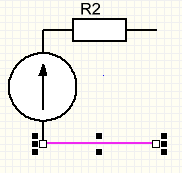
Перенос источника через узел

Преобразование соединения схемы звезды и треугольник

3.2. Методы расчета электрических цепей
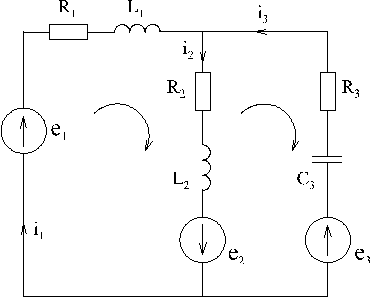
Расчет резистивных цепей методом составления уравнений Кирхгофа.
С помощью законов Кирхгофа можно рассчитать токи в сколь угодно сложных цепях. Для этого необходимо проделать следующее: определить количество ветвей в заданной цепи; задаться предполагаемыми токами во всех ветвях и направлениями обходов в контурах (например, по часовой стрелке); по первому закону составитьn-1 уравнений, где n – количество узлов цепи; определить количество элементарных контуров в цепи; составить по второму закону Кирхгофа m уравнений, где m – число элементарных контуров.
В полученную систему уравнений подставить числовые значения и любым методом рассчитать неизвестные в ветвях токи.
Метод суперпозиции(наложения) основан на принципе независимости действия электродвижущих сил различных источников. Он применим только к линейным цепям, т.е. таким, сопротивление которых не зависит от величины протекающего тока или приложенного напряжения. Процессы в этих цепях описываются уравнениями первой степени.
Метод контурных токов дает возможность определять токи в цепи с помощью стольких уравнений, сколько элементарных контуров имеет цепь.
Контурные токи являются условными алгебраическими величинами, одинаковыми по величине для всех участков данного контура. Направления их выбирают произвольно и показывают в электрических схемах дугообразными стрелками индексами.
Метод эквивалентного генератора используется для определения тока, напряжения или мощности в одной ветви сложной эквивалентной цепи. При этом всю остальную часть сложной цепи, к которой подключена данная ветвь, представляют в виде двухполюсника.
Этот метод базируется на теореме Тевенина, согласно которой по отношению к выделенной ветви при расчете двухполюсник можно заменить эквивалентным генератором, ЭДС которого равна напряжению холостого хода на зажимах выделенной ветви, а внутреннее сопротивление равно входному сопротивлению двухполюсника.
Метод узловых потенциалов - метод расчета электрических цепей путём записи системы линейных алгебраических уравнений, в которой неизвестными являются потенциалы в узлах цепи. В результате применения метода определяются потенциалы во всех узлах цепи, а также, при необходимости, токи во всех ветвях. Метод узловых потенциалов применяется к эквивалентной схеме, поэтому имеют силу те же ограничения, что и для применимости эквивалентных схем. Если изначально дана реальная схема, то для неё необходимо составить эквивалентную схему и дальнейший расчет производить с ней. Таким образом, схема, к которой применяется метод узловых потенциалов, не содержит никаких реальных элементов.
Уравнение для узла:
![]()