4.3 Математические модели дискретных (цифровых) сау

Структурная схема цифровой САУ представлена на рис. 4.1. Она включает в себя непрерывную часть системы (управляемый объект, датчики и исполнительные механизмы) с передаточной функцией и управляющую ЦВМ, реализующую заданный закон управления в соответствии с некоторой дискретной передаточной функцией.

В отличие от непрерывных САУ здесь сигналы, поступающие в ЦВМ, принимают дискретные значения в дискретные моменты времени. Квантование по времени представляет собой периодический процесс, характеризующийся тактом дискретности Т₀ .На рис. 4.1этот процесс осуществляется с помощью импульсного ключа, который замыкается на короткое время с шагом дискретностиТ₀ ,производит отсчеты амплитуды непрерывного сигнала в моменты времени Далее в аналого-цифровом преобразователе (АЦП) значения амплитуд непрерывного сигнала преобразуются в цифровой код, т.е. осуществляется процесс квантования сигналов по уровню с шагом квантования, определяемым разрядностью АЦП. Преобразованные входные данные поступают далее в ЦВМ, где они обрабатываются по запрограммированным алгоритмам, в результате чего формируются выходные данные, т.е. ЦВМ реализует некоторый цифровой фильтр. По отношению к дискретным отсчетам входных данных выходные данные формируются с задержкой.Эта задержка равна времени, затрачиваемому на аналого-цифровое преобразование сигналов, поступающих с датчиков, и последующую их обработку в ЦВМ. В структурной схеме это учитывается путем включения в контуры управления звеньев чистого запаздывания с передаточной функцией.Так как интервалы, обычно значительно меньше постоянных времени непрерывной части САУ, ими, как правило, пренебрегают.

Так как исполнительные механизмы цифровых САУ обычно имеют аналоговый вход, выходные данные ЦВМ поступают на вход цифро-аналогового преобразователя (ЦАП), осуществляющего преобразование цифрового кода в непрерывный сигнал. Данный процесс преобразования обычно включает в себя две операции: декодирование – преобразование числового кода в импульсный сигнал с амплитудно-импульсной модуляцией и экстраполяцию – преобразование импульсного сигнала в аналоговый сигнал.

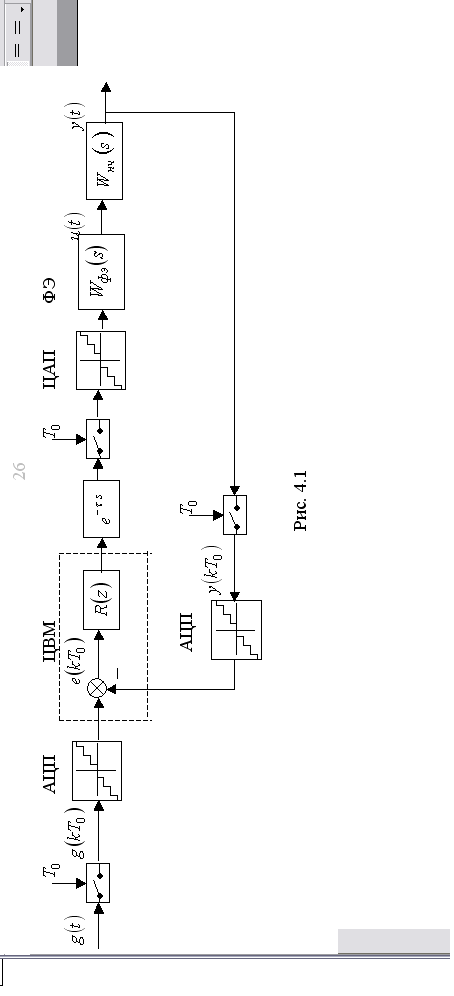
Процесс декодирования сопровождается квантованием сигналов по уровню в соответствии со статической характеристикой ЦАП. При этом, нелинейный эффект квантования (см. рис. 4.1)обусловлен тем, что число разрядов управляющей ЦВМ обычно больше, чем у ЦАП, а это эквивалентно внесению ошибок округления.

Процесс экстраполяции, как правило, представляет собой фиксацию выходного сигнала ЦВМ на одном уровне в течение периода дискретности T₀ .На рис. 4.1 процессу экстраполяции соответствует фиксирующий элемент (ФЭ) с передаточной функцией.

В ряде случаев для лучшего сглаживания выходных сигналов ЦВМ, кроме фиксации, могут использоваться и другие виды экстраполяции (линейная, квадратичная и т. п.).

Таким образом, в цифровых САУ обрабатываемые сигналы подвергаются квантованию по уровню на трёх этапах: в АЦП, ЦВМ и ЦАП, что является причиной возникновения нелинейностей. Как известно, теоретический анализ влияния даже одной нелинейной характеристики на динамические и статические свойства САУ сопряжён со значительными трудностями. Тем более сложную задачу представляет исследование всех эффектов, связанных с квантованием по уровню в цифровом контуре управления. При исследовании таких систем обычно предполагают, что ошибки квантования случайны и распределены по равномерному закону, либо просто рассматривается наихудший вариант, когда все ошибки квантования принимают максимально возможные значения. Однако, наиболее достоверным и универсальным средством для анализа подобных нелинейностей является математическое моделирование.

Математическая модель АЦП обычно представляется в виде схемы (рис. 4.2), где - ошибка управления;- дискретные значения сигналав моменты времени- шум квантования;- шаг квантования по уровню, определяемый разрядностью АЦП;

- сигнал на выходе АЦП.

Рис. 4.2

Разрядность АЦП выбирают таким образом, чтобы погрешность квантования была меньше статических и динамических ошибок датчиков. При этом разрядность ЦАП должна быть согласована с разрядностью АЦП. Целесообразно задавать её такой, чтобы изменение управляющей переменной на один шаг вызывало (после прохождения через непрерывную часть системы) изменение кода в АЦП на единицу младшего разряда. Учитывая также, что разрядность современных управляющих ЦВМ значительно превышает разрядность слов АЦП и ЦАП, нежелательные явления, обусловленные квантованием по уровню в цифровых контурах управления, могут быть практически устранены. В связи с этим, в дальнейшем эффекты квантования по уровню в цифровых САУ не учитываются и рассматриваются сигналы, дискретные только во временной области.

Непрерывная часть цифровой САУ в совокупности с ЦАП образуют так называемую приведённую непрерывную часть (ПНЧ) цифровой системы. При этом, уравнения ЦАП и непрерывной части цифровой САУ соответствуют структурной схеме (рис. 4.3), где

- дискретные отсчёты сигнала управления;- выход идеального импульсного элемента (ИИЭ), т. е. амплитудно-модулированная последовательность-функций;

- передаточная функция фиксирующего элемента ФЭ;

- последовательность прямоугольных импульсов длительностис амплитудамив дискретные моменты времени;

- передаточная функция непрерывной части системы (НЧ) ; - выход САУ.

T₀ИИЭ ФЭ НЧ

u(t)

ПНЧ

Рис. 4.3

Зависимость между изаписывается в виде

(4.33)

где - весовая функция приведённой непрерывной части (ПНЧ) САУ, включающей в себя ФЭ и НЧ. В дискретные моменты времени:

(4.34)

Переходя к z-преобразованию, можно перейти от уравнения (4.34) к выражению:

(4.35)

где

Дискретная передаточная функция ПНЧ в уравнении (4.35) может быть найдена с помощью соотношения:

(4.36)

где символ означаетz-преобразование для переходной функциинепрерывной части САУ, изображение по Лапласу которой равно. Как правило, при вычислениипо формуле (4.36) удобнее представить изображениев виде суммы простейших дробей, после чего уже воспользоваться известными правиламиz-преобразования.

Синтез передаточной функции цифрового регулятора (дискретного корректирующего устройства) осуществляется прямыми методами или на основе аналогового прототипа []. В последнем случае предварительно находится передаточная функцияаналогового прототипа, после чего производится замена(метод «прямоугольников») или(метод «трапеций» или преобразование Тастина). Полученная таким образом передаточная функция

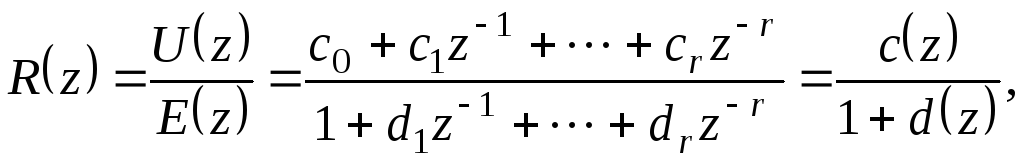(4.37)

связывает между собой изображение сигнала ошибки и управляющего воздействия, что эквивалентно разностному уравнению

(4.38)

где

Пример 4.1. Пусть непрерывная часть САУ (см. рис. 4.3) имеет передаточную функцию

В результате синтеза аналогового корректирующего устройства (аналогового прототипа) по желаемой передаточной функции замкнутой САУ

получаем

Используя преобразование Тастина, из последнего выражения находим дискретную передаточную функцию цифрового корректирующего устройства (для T₀=0,025 с)

Соответствующее разностное уравнение имеет вид:

Для динамических систем произвольного порядка z-передаточ- ная функция разомкнутой САУ имеет вид

(4.39)

При этом для статических дискретных систем в соответствии с теоремой о конечном значении можно определить статический коэффициент передачи

(4.40)

Для астатических систем -го порядка астатизма дискретная передаточная функция имеет приz = 1полюс-й кратности:

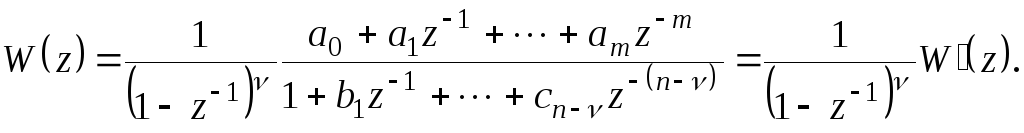(4.41)

Астатический коэффициент передачи определяется соотношением

(4.42)

Нетрудно показать,что степень полинома знаменателяпоравна степени полинома знаменателяпо, изменение нулей вменяет лишь числительи не оказывает влияния на знаменатель, а изменение знаменателяполностью изменяет.

Введем понятие дискретной передаточной функции применительно к цифровым многосвязным САУ.

Матричная структурная схема дискретной многосвязной САУ показана на рис. 4.4. Здесьпередаточная матрица многосвязного объекта управления (непрерывная часть многосвязной САУ);R(z) - передаточная матрица дискретного регулятора, определяющая связь между изображениями его входа и выхода.

ФЭ НЧ

g e u y

Рис. 4.4

Рассматривая выходные величины (i=1,…,p; p - число выходов НЧ) многосвязной САУ в дискретные моменты времени z-передаточную матрицу приведённой непрерывной части системы с учетом фиксирующих элементов ФЭ можно записать в виде

где символ означаетz-преобразование для матричной переходной функциимногосвязного объекта управления, которая, в свою очередь, является оригиналом для изображения по Лапласу, т.е.

Выражение

(4.43)

можно рассматривать как дискретную передаточную матрицу многосвязной САУ в разомкнутом состоянии. Соответственно дискретная передаточная матрица Ф(z) замкнутой системы определяется соотношением

(4.44)

откуда следует, что характеристическое уравнение замкнутой дискретной МСАУ имеет вид

(4.45)

Другой способ определения передаточной функции системы дает описание дискретной САУ в терминах переменных состояния.

Действительно, по аналогии с непрерывными системами дискретные системы в целом или отдельные их части могут быть описаны системами векторных конечно-разностных уравнений вида

(4.46)

где x -n-мерный вектор состояния системы;g-m-мерный вектор задающих воздействий (входов) системы;y p-мерный вектор управляемых координат; матрицы соответствующих размерностей:

A - собственная-матрица системы,B -матрица управления,С - -матрица выхода.

Применив операцию z-преобразования к уравнениям (4.46),получим

(4.47)